Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "Формулы Приведения"
Содержание
- 1. Презентация по теме "Формулы Приведения"
- 2. Например: sin (π+α) = - sin α
- 3. sin (π+α) = - sin α
- 4. sin (π+α) = - sin α
- 5. Слайд 5
- 6. Например: упростить sin (3π/2+α)
- 7. Упростить: sin (π+α) =
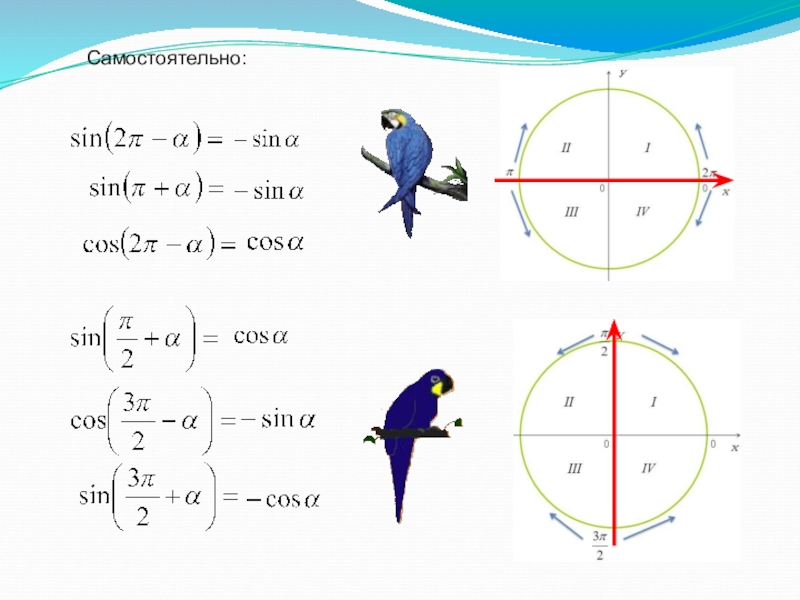
- 8. Самостоятельно:
- 9. Применение формул приведения :Для вычислений:
- 10. Применение формул приведения :Для упрощения выражений:
- 11. Применение формул приведения :Докажите эти равенства разными
- 12. Применение формул приведения :Самостоятельно. Упростить выражения:
- 13. Подведем итоги:Что нового узнали на уроке?Чему научились?Какое правило запомнили?Для чего применяются формулы приведения?
- 14. Скачать презентанцию
Например: sin (π+α) = - sin α cos (3π/2+α) = sin α Будем считать, что угол α – угол I четверти, т.е.
Слайды и текст этой презентации
Слайд 1ФОРМУЛЫ ПРИВЕДЕНИЯ
Позволяют вычислить значения тригонометрических функций угла любой четверти через
угол I четверти
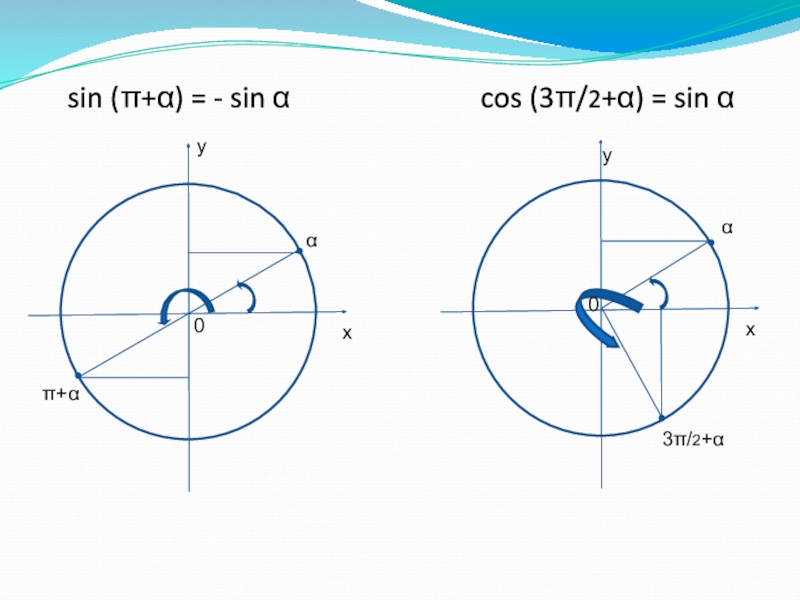
Е.В. Учитель математики
Слайд 2Например: sin (π+α) = - sin α
cos (3π/2+α) = sin
αБудем считать, что угол α – угол I четверти, т.е. α˂π/2
II
III
IV
I
II
III
IV
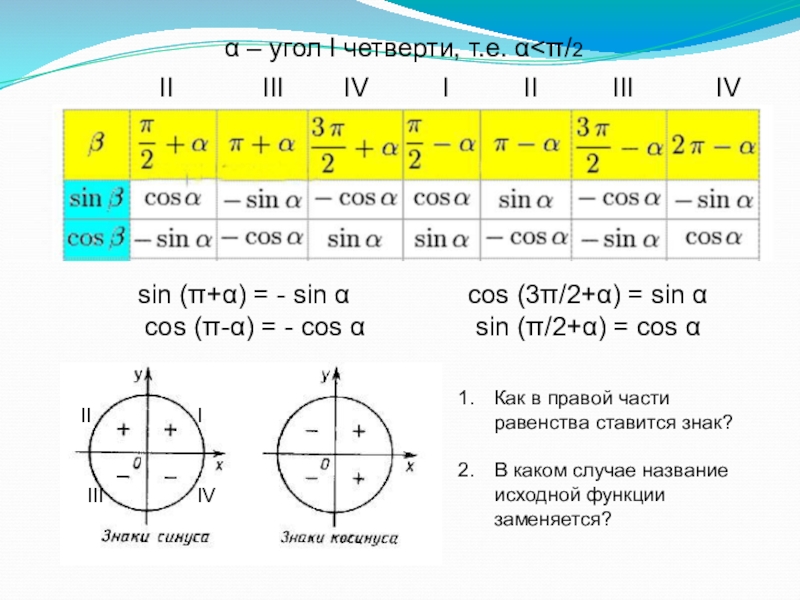
Слайд 4sin (π+α) = - sin α
cos (3π/2+α) = sin α
cos (π-α) =
- cos α sin (π/2+α) = cos α α – угол I четверти, т.е. α˂π/2
II III IV I II III IV
II I
III IV
Как в правой части равенства ставится знак?
В каком случае название исходной функции заменяется?
Слайд 5
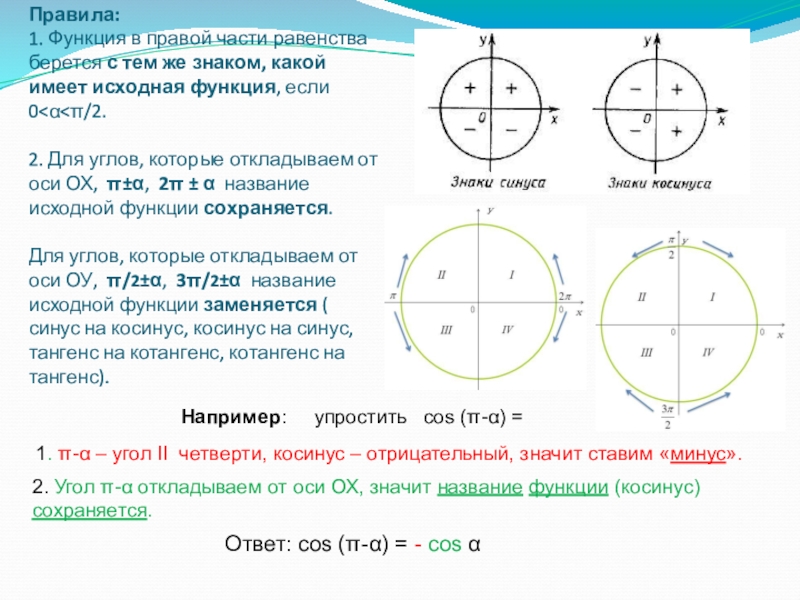
Правила: 1. Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если 0<α<π/2. 2. Для углов, которые откладываем от оси ОХ, π±α, 2π ± α название исходной функции сохраняется. Для углов, которые откладываем от оси ОУ, π/2±α, 3π/2±α название исходной функции заменяется ( синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
Ответ: cos (π-α) = - cos α
Например: упростить cos (π-α) =
1. π-α – угол II четверти, косинус – отрицательный, значит ставим «минус».
2. Угол π-α откладываем от оси ОХ, значит название функции (косинус) сохраняется.
Слайд 6Например: упростить sin (3π/2+α) =
1. 3π/2+α
– угол IV четверти, синус – отрицательный, значит ставим «минус».
2.
Угол 3π/2+α откладываем от оси ОУ, значит название функции (синус) меняется на косинус.Ответ: sin (3π/2+α) = - cos α
Правила:
1. Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если 0<α<π/2.
2. Для углов, которые откладываем от оси ОХ, π±α, 2π ± α название исходной функции сохраняется.
Для углов, которые откладываем от оси ОУ, π/2±α, 3π/2±α название исходной функции заменяется ( синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
Слайд 7Упростить:
sin (π+α) =
1). π+α
– угол … четверти, синус в этой четверти имеет знак
…2). Угол π+α откладываем от оси …, значит название функции (синус) …
Ответ: sin (π+α) = - sin α
cos (3π/2+α) =
1). В какой четверти угол?
2). От какой оси откладываем угол? Менять ли название функции?
Ответ: cos (3π/2+α) = sin α
sin (3π/2-α) =
1). В какой четверти угол?
2). От какой оси откладываем угол? Менять ли название функции?
Ответ: sin (3π/2-α) = - cos α
Слайд 11Применение формул приведения :
Докажите эти равенства разными способами
(с помощью
изученных правил и пользуясь определением тангенса и котангенса).
Слайд 13Подведем итоги:
Что нового узнали на уроке?
Чему научились?
Какое правило запомнили?
Для чего
применяются формулы приведения?
