Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по алгебре 11 класс "Показательная функция, ее свойства и графики"
Содержание
- 1. Презентация по алгебре 11 класс "Показательная функция, ее свойства и графики"
- 2. Содержание Понятие функции у = аxПрименение показательной функцииСвойства показательной функцииГрафик показательной функцииПоказательные уравненияПоказательные неравенства
- 3. Понятие показательной функции.Функцию вида y = ах,
- 4. 1) Например, в теории межпланетных путешествий решается
- 5. 2) Радиоактивный распад вещества задаётся формулой
- 6. 3) Изменение атмосферного давления p в зависимости
- 7. 3) Изменение атмосферного давления p в зависимости
- 8. an ∙ am = an + m an
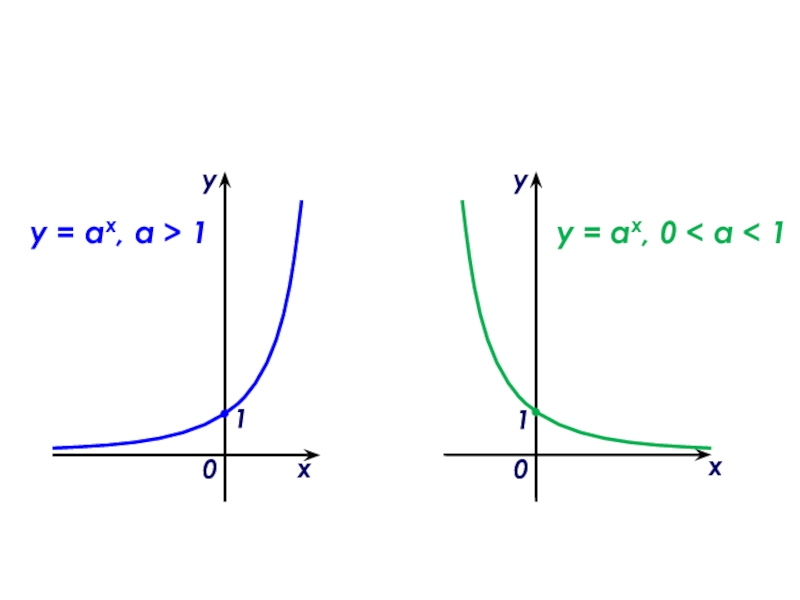
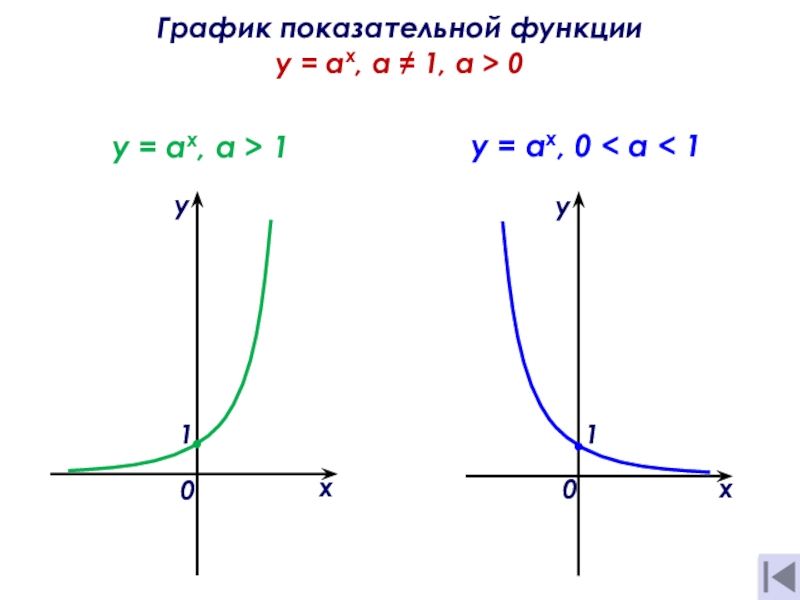
- 9. График показательной функции y = ах,
- 10. Если 0 < а < 1, то
- 11. Показательные уравненияУравнения вида af(x) = аh(х), где
- 12. Показательные уравнения. Примеры Пример 1Пример 2Пример 3
- 13. Показательные уравнения. Примеры Пример 4Пример 5
- 14. Показательные уравнения. Примеры Пример 6
- 15. Показательные уравнения. Примеры Пример 7
- 16. Показательные уравнения. Примеры Пример 8
- 17. Показательные уравнения. Примеры Пример 9 (однородное уравнение)
- 18. Показательные уравнения. Примеры Пример 10 (составление отношения)
- 19. Показательные уравнения. Примеры Пример 11 (скрытая замена переменной)+ = 4
- 20. Показательные уравнения. Примеры Пример 11 (скрытая замена переменной)+ = 4
- 21. Показательные неравенстваНеравенства вида af(x) > аh(х), где
- 22. Показательные неравенства. ПримерыПример 1Пример 2
- 23. Показательные неравенства. ПримерыПример 3
- 24. Показательные неравенства. ПримерыПример 4
- 25. Показательные неравенства. ПримерыПример 4
- 26. Используемые материалыАлгебра и начала анализа. 11 класс.
- 27. Скачать презентанцию
Содержание Понятие функции у = аxПрименение показательной функцииСвойства показательной функцииГрафик показательной функцииПоказательные уравненияПоказательные неравенства
Слайды и текст этой презентации
Слайд 2Содержание
Понятие функции у = аx
Применение показательной функции
Свойства показательной функции
График
показательной функции
Слайд 3Понятие показательной функции
.
Функцию вида
y = ах, где а ≠
1, a > 0
называют
показательной функцией
Слайд 41) Например, в теории межпланетных путешествий решается задача об определении
массы топлива, необходимого для того, чтобы придать ракете нужную скорость
v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости vo, с которой продукты горения вытекают из ракетного двигателя. Если не учитывать сопротивление воздуха и притяжение Земли, то массаПоказательная функция часто используется при описании различных физических процессов
топлива определяется формулой:
М = m(ev/vo-1) (формула К.Э. Циолковского).
Например, для того чтобы ракета с массой 1,5т имела скорость 8000м/с, надо взять примерно 80т топлива.
Слайд 52) Радиоактивный распад вещества задаётся формулой m =
m0(1/2)t/tо, где m и mо – масса радиоактивного вещества в
момент времени t и в начальный момент времени t = 0; T - период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое).Показательная функция часто используется при описании различных физических процессов
Когда радиоактивное вещество распадается, его количество уменьшается.
Через некоторое время остаётся половина первоначального количества вещества. Чем больше период полураспада, тем медленнее распадается вещество.
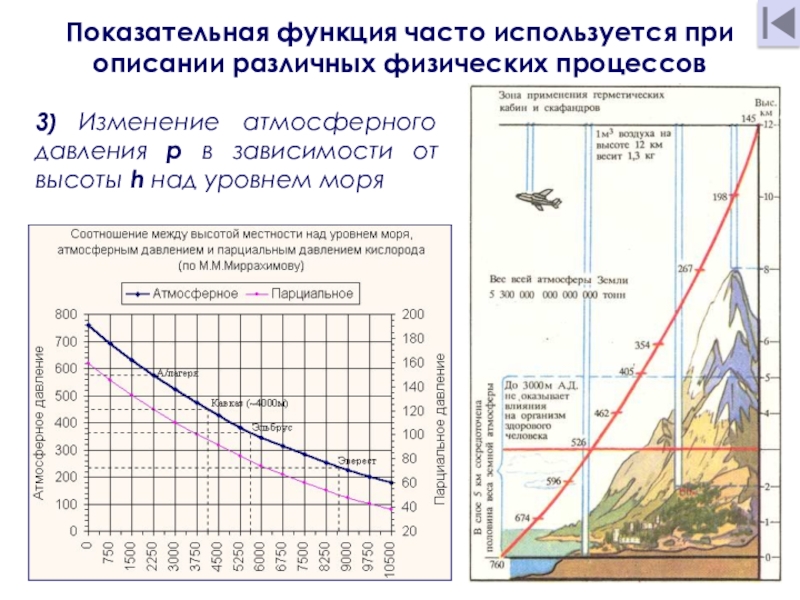
Слайд 63) Изменение атмосферного давления p в зависимости от высоты h
над уровнем моря описывается формулой p = pо ∙
ak, где pо – атмосферное давление над уровнем моря, а – некоторая постоянная.Показательная функция часто используется при описании различных физических процессов
Барограф метеорологический
анероидный
Погодная станция Oregon Scientific
Слайд 73) Изменение атмосферного давления p в зависимости от высоты h
над уровнем моря
Показательная функция часто используется при описании различных физических
процессов
Слайд 8an ∙ am = an + m
an : am =
an − m
(an)m = anm
(ab)n = an ∙ bn
(a :
b)n = an : bnа) При а > 1 функция возрастает на R;
б) при 0 < а < 1 функция убывает на R.
а) Нулей не имеет;
б) точка пересечения с осью ординат (0; 1),
т. к. у(0) = а0 = 1.
Свойства показательной функции y = ах, а ≠ 1, a > 0
Ни четная функция, ни нечетная.
D(y) = (-∞; +∞),
E(y) = (0; +∞).
.
Не ограничена сверху, ограничена снизу.
Не имеет ни наибольшего, ни наименьшего значений.
Непрерывна. Выпукла вниз.
" alt="График показательной функции y = ах, а ≠ 1, a > 0ху0y = ах, а >">Слайд 10Если 0 < а < 1, то
a) неравенство ax
> 1 справедливо ⟺ x < 0;
б) неравенство ax
< 1 справедливо ⟺ x > 0. Свойства сравнения выражений вида ах, а ≠ 1, a > 0
Если 0 < а < 1 или а > 1, то равенство ar = as справедливо тогда и только тогда, когда r = s.
.
Если а > 1, то
a) неравенство ax > 1 справедливо ⟺ x > 0;
б) неравенство ax < 1 справедливо ⟺ x < 0.
Если а > 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) > h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) < h(x).
Если 0 < а < 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) < h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) > h(x).
" alt="Если 0 < а < 1, то a) неравенство ax > 1 справедливо ⟺ x < 0;">Слайд 11
Показательные уравнения
Уравнения вида af(x) = аh(х), где а ≠ 1,
a > 0
называют показательными уравнениями
af(x) = аh(х)
f(x)
= h(х)⟺
Методы решения показательных уравнений:
Функционально-графический метод.
Метод уравнивания показателей.
Метод введения новой переменной.
Слайд 21
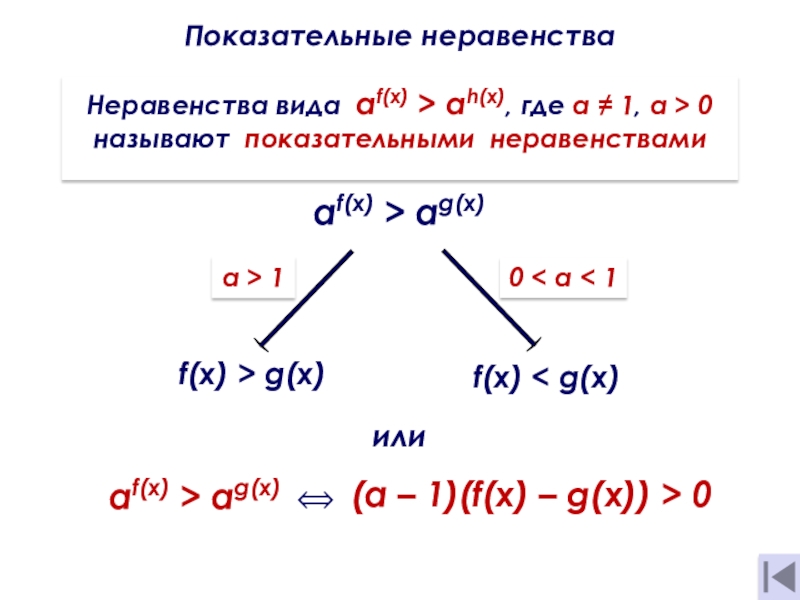
Показательные неравенства
Неравенства вида af(x) > аh(х), где а ≠ 1,
a > 0
называют показательными неравенствами
af(x) > аg(х)
f(x) > g(х)
f(x)
< g(х)0 < а < 1
а > 1
af(x) > аg(х) ⟺
(а – 1)(f(x) – g(x)) > 0
или
аh(х), где а ≠ 1, a" alt="Показательные неравенстваНеравенства вида af(x) > аh(х), где а ≠ 1, a > 0 называют показательными неравенствамиaf(x) >">
Слайд 26
Используемые материалы
Алгебра и начала анализа. 11 класс. В 2 ч.
Ч. 1. Учебник для общеобразоват. учреждений (профильный уровень) / А.Г.
Мордкович, П.В. Семенов. 2-е изд., стер. – М.: Мнемозина, 2008http://www.physics.org/ -
http://www.mathematics.ru/courses/algebra/design/index.htm -
http://www.megabook.ru/index.asp - Большая энциклопедия Кирилла и Мефодия
