Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Работа по математике "Магические квадраты"
Содержание
- 1. Работа по математике "Магические квадраты"
- 2. «Составление магических квадратов, представляет собой превосходную умственную
- 3. Цель работы: изучить магические квадраты и его
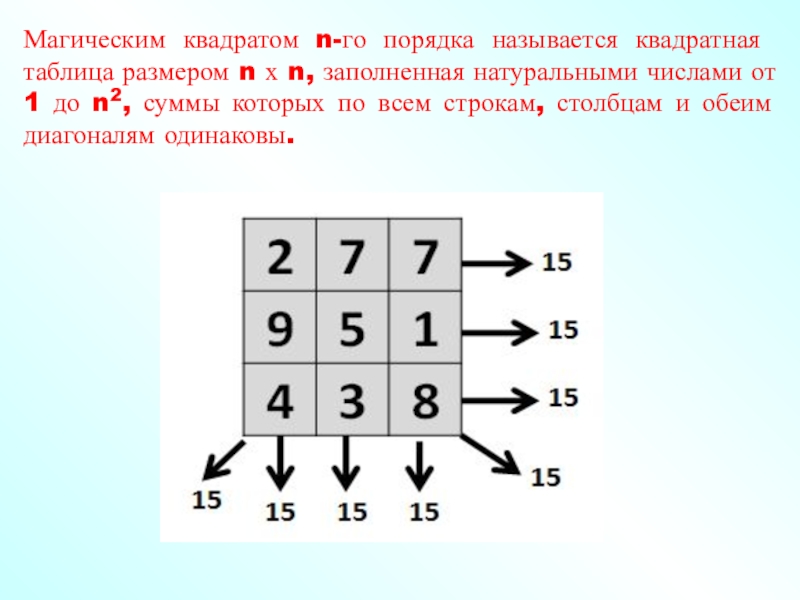
- 4. Магическим квадратом n-го порядка называется квадратная таблица
- 5. Основные понятия Главная диагональ –
- 6. Первые значения магических констант приведеныв следующей таблице:Сумма
- 7. История возникновения магических квадратов Магический
- 8. Магическим квадратам приписывали различные мистические свойства. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Мистические амулеты
- 9. Квадрат Дюрера
- 10. Один из наиболее известных магических квадратов –
- 11. Магического квадрата 2-го порядка не существуетКак ни
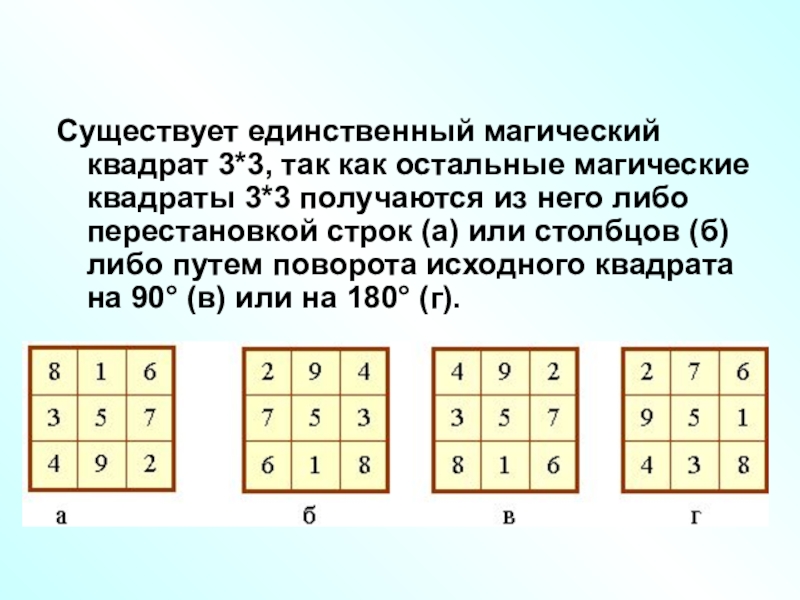
- 12. Существует единственный магический квадрат 3*3, так как
- 13. Латинские квадратыесли один квадрат наложить на другой,
- 14. Старинная занимательная задача Эйлера: «Среди 36 офицеров
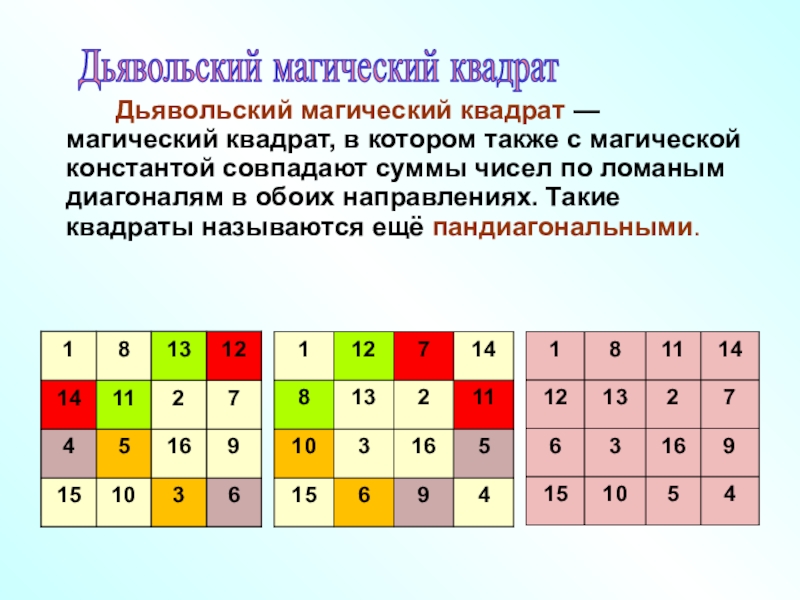
- 15. Дьявольский магический квадрат — магический квадрат, в
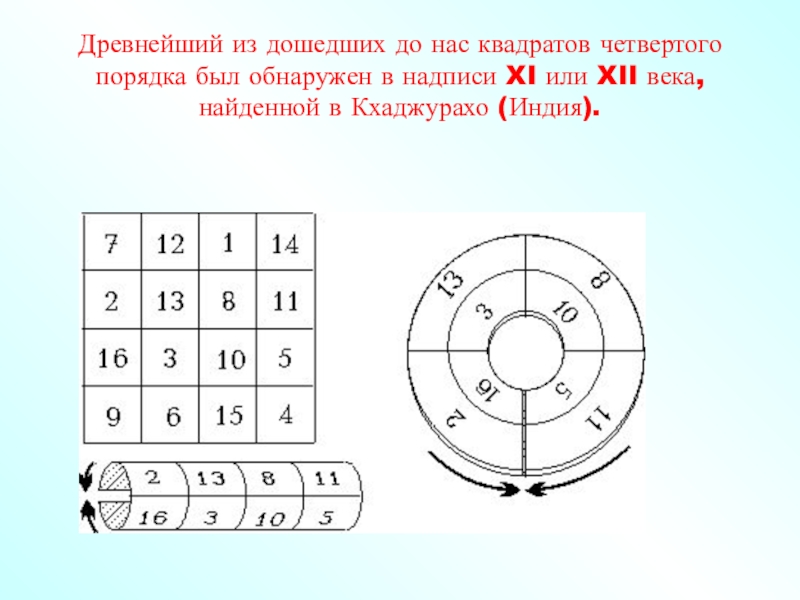
- 16. Древнейший из дошедших до нас квадратов четвертого
- 17. Квадраты, у которых суммы чисел, расположенные на
- 18. Если пандиагональный квадрат еще и ассоциативный, то он носит название идеальный. Пример идеального магического квадрата:Идеальный квадрат
- 19. Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных
- 20. Квадрат, в котором любые два числа, расположенные
- 21. Бенджамин Франклин
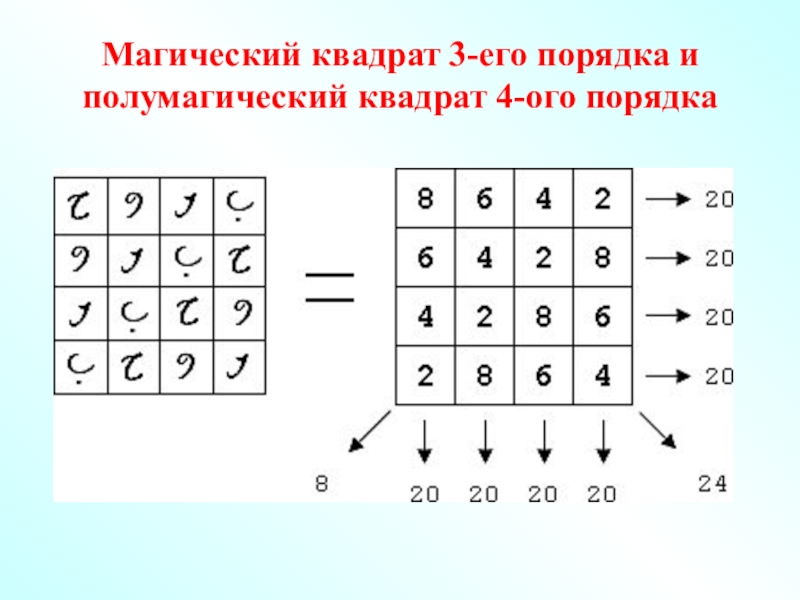
- 22. Магический квадрат 3-его порядка и полумагический квадрат 4-ого порядка
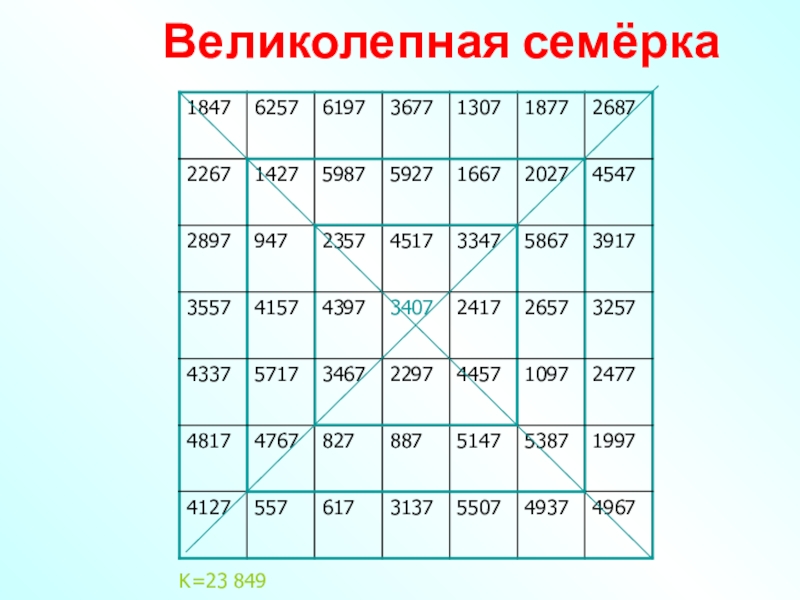
- 23. Великолепная семёркаK=23 849
- 24. Применение магических и латинских квадратов
- 25. Слайд 25
- 26. Магические квадраты и «магия планет»Каждой планете соответствует
- 27. Магические квадраты и «магия планет»В квадрате Солнца —
- 28. ШифрованиеМЮЛИИОВДКПОРЧОКК
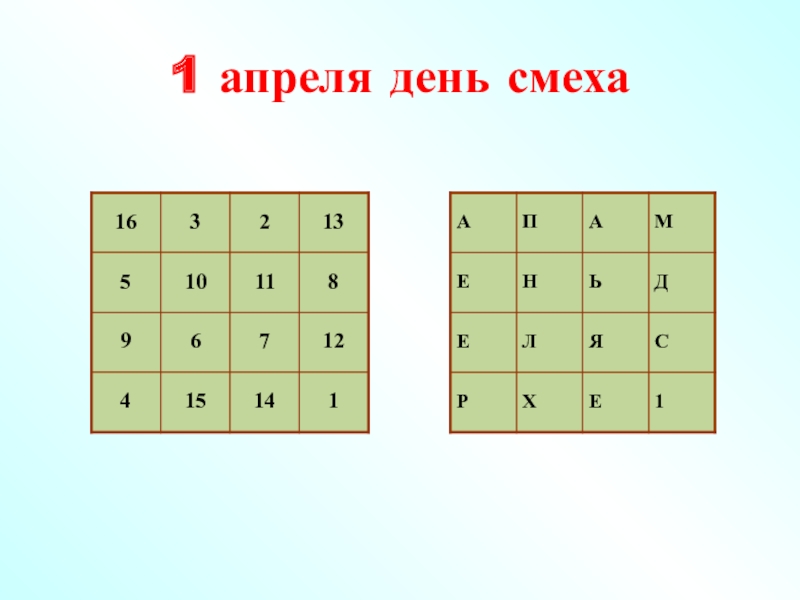
- 29. 1 апреля день смеха
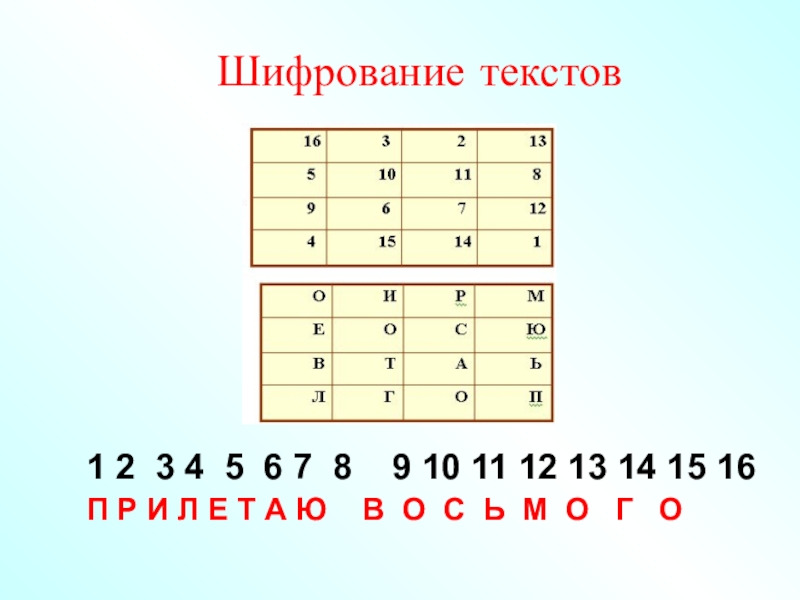
- 30. Шифрование текстов 1 2 3 4 5
- 31. Судо́ку — это головоломка-пазл
- 32. Какуро
- 33. Игра шаффлборд очень популярна в Англии среди аристократов.
- 34. Фэн шуй – это древнекитайское искусство, которое
- 35. Тайный сад. Феншуй. Тайный сад - это
- 36. Слайд 36
- 37. Цифры, стоящие в клетках рисунка, означают:
- 38. Старинная занимательная задача Эйлера: «Среди 36 офицеров
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Квадрат Пифагора
- 43. Моя дата рождения 13.04.1995 1)Сложим цифры даты
- 44. Клетки имеют следующие значения: 1. Характер
- 45. Значение ячеек квадратаЯЧЕЙКА 1 – целеустремлённость, воля,
- 46. ЯЧЕЙКА 4 – здоровье. Это связаноэкгрегором, то
- 47. ЯЧЕЙКА 7 – мера таланта. 7 –
- 48. По этой таблице видно, что у мужчин
- 49. Виды магических квадратов
- 50. Метод построения магических квадратов
- 51. Магические квадраты четного порядка Порядок которого равен степени числа 2
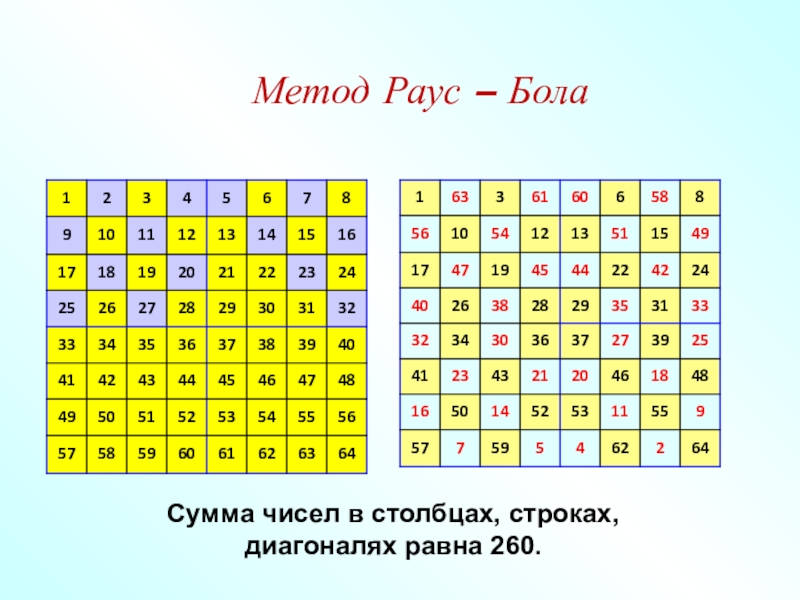
- 52. Метод Раус – Бола Сумма чисел в столбцах, строках, диагоналях равна 260.
- 53. 123456789Прием составления нечетных магических квадратов (3*3, 5*5,
- 54. 12345678910111213141516211718192022232425126111264510162120222425
- 55. 37891213141517181923111264510162120222425Получится магический 25-клеточный квадрат:
- 56. Метод А. де ЛубераЧисло 1 помещается в
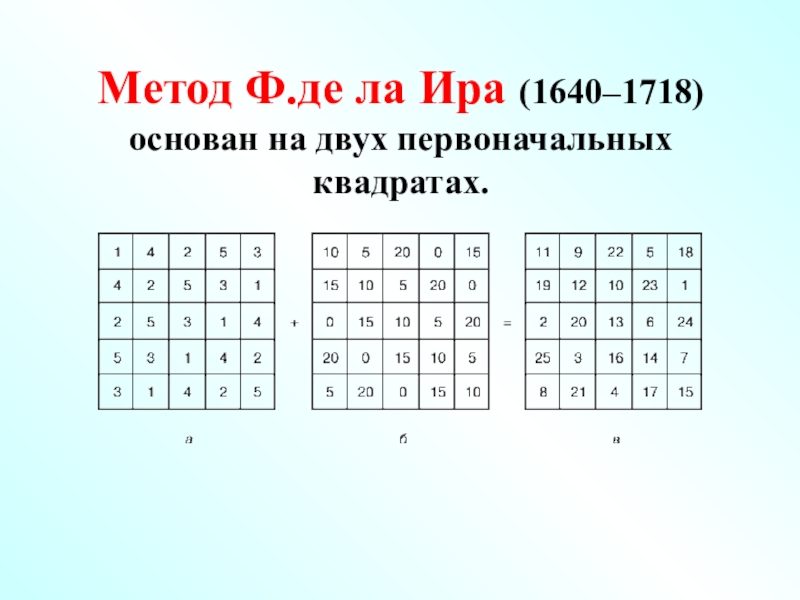
- 57. Метод Ф.де ла Ира (1640–1718) основан на двух первоначальных квадратах.
- 58. 3)4)
- 59. Магические квадраты нечетного порядка
- 60. Метод достроения Шаг 2. Полученная на
- 61. Метод достроения Шаг 3. Каждое число,
- 62. В левом верхнем квадрате порядка 5 выделить
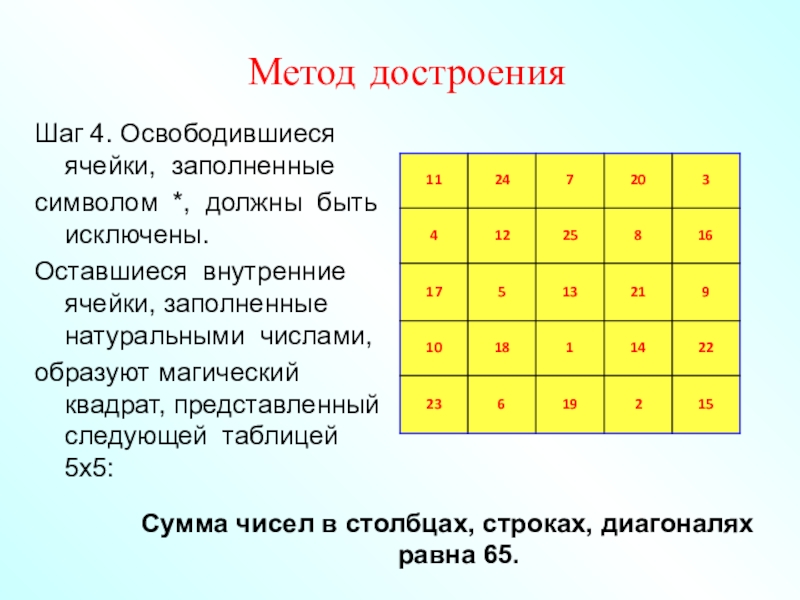
- 63. Метод достроенияШаг 4. Освободившиеся ячейки, заполненные символом
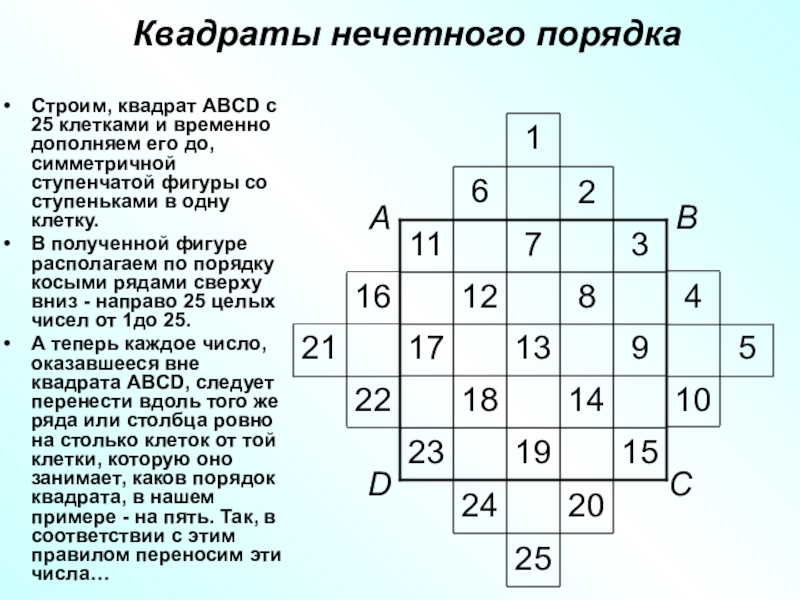
- 64. Квадраты нечетного порядкаСтроим, квадрат ABCD с 25
- 65. Четно – нечетные квадраты Диагональный метод Получится четно-нечетный магический квадрат с суммой, равной 505.
- 66. Построение магических квадратовМетод террасДля заданного нечетного N
- 67. Метод А.де ла Лубера (французского геометра 17
- 68. Известно, что шахматы, как и магические квадраты,
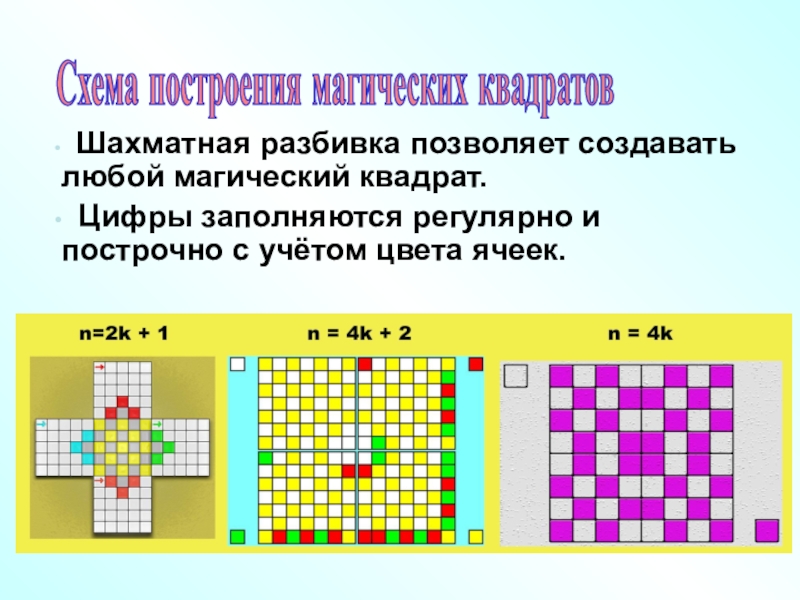
- 69. Шахматная разбивка позволяет создавать любой магический
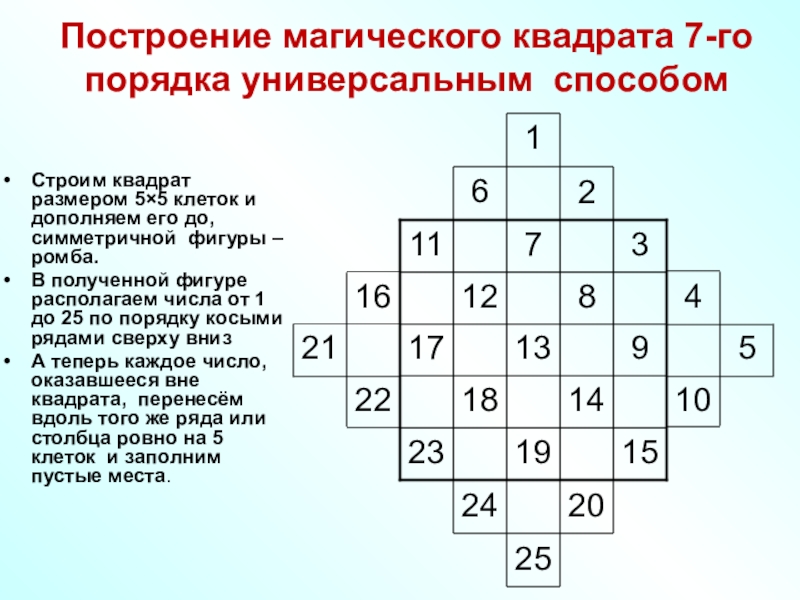
- 70. Построение магического квадрата 7-го порядка универсальным способом
- 71. Исторически значимые магические квадраты
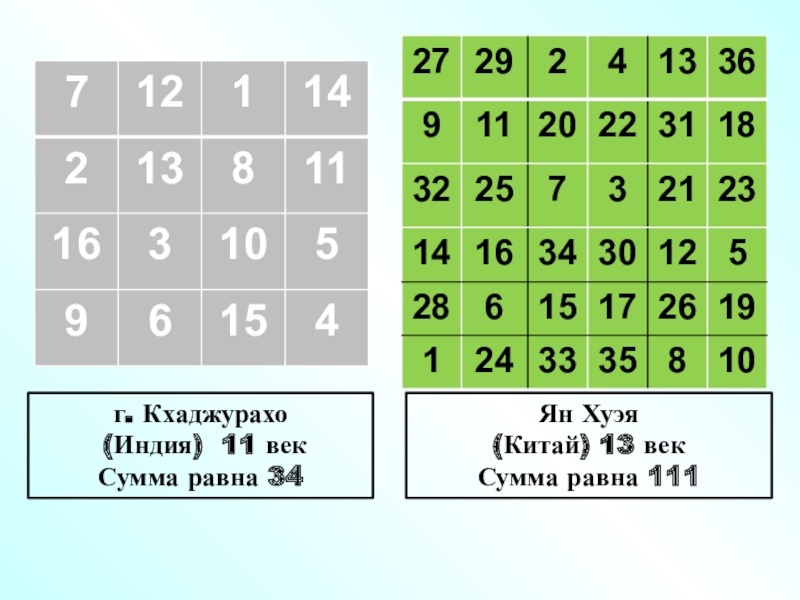
- 72. г. Кхаджурахо (Индия) 11 векСумма равна 34Ян Хуэя (Китай) 13 векСумма равна 111
- 73. Квадрат Ло-Шу Ло Шу (кит. трад. 洛書,
- 74. В XIII в. математик Ян Хуэй занялся
- 75. Квадрат, найденный в Кхаджурахо (Индия)Самый ранний уникальный
- 76. Магический квадрат Ян Хуэя (Китай)В 13 в.
- 77. Квадраты Генри Э. Дьюдени и Аллана У.
- 78. Квадрат Альбрехта ДюрераФрагмент гравюры Дюрера «Меланхолия»Магический квадрат
- 79. Магический квадрат ЭйлераЭтот квадрат 8 порядка составлен
- 80. Квадрат Багуа Магический квадрат в фэн-шуй
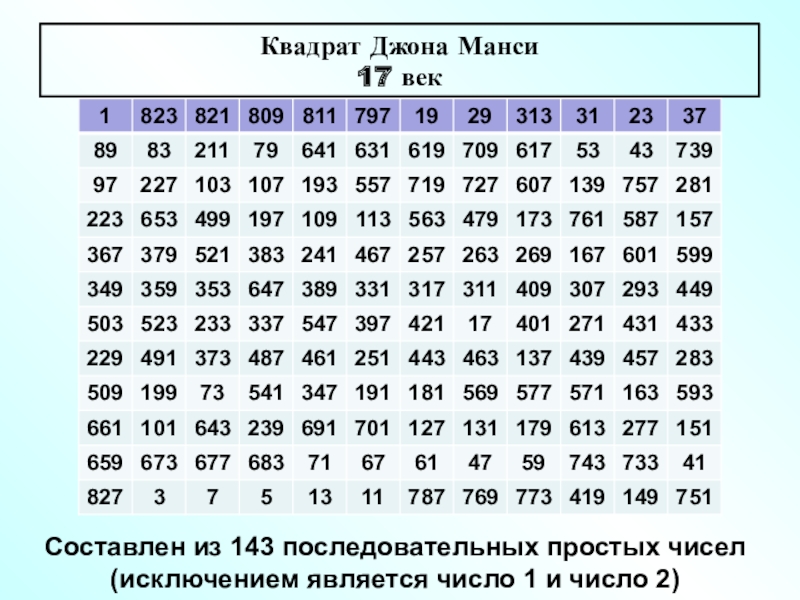
- 81. Квадрат Джона Манси17 векСоставлен из 143 последовательных простых чисел (исключением является число 1 и число 2)
- 82. Просто КВАДРАТ и никаких фокусов. Предположительно слово «Абракадабра»
- 83. Средневековый букволабиринт
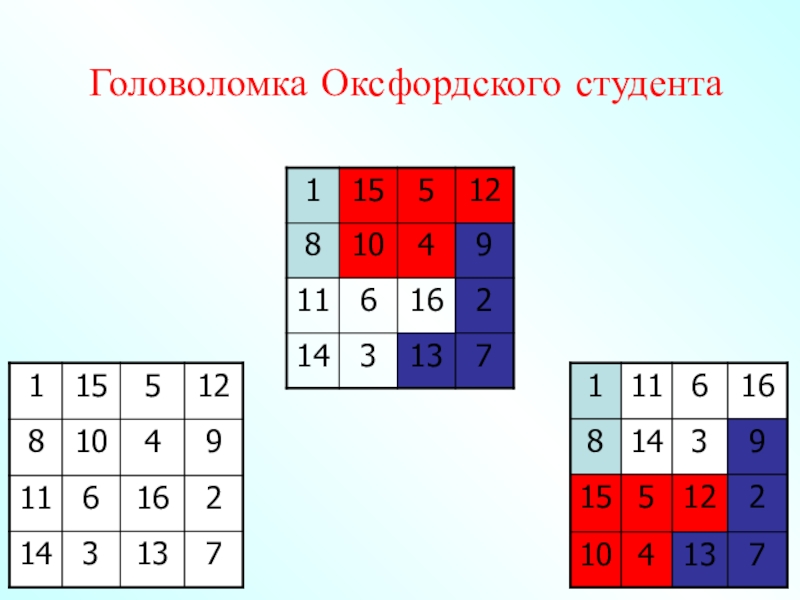
- 84. Головоломка Оксфордского студента
- 85. Решение задач
- 86. Трудные задачиПростым числам было посвящено множество занимательных
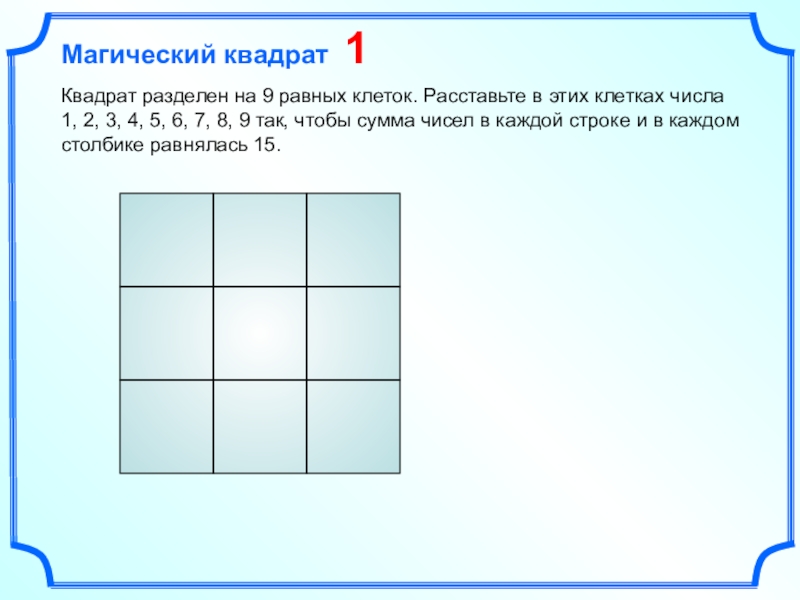
- 87. Квадрат разделен на 9 равных клеток. Расставьте
- 88. 123456789Магический квадрат 3-го порядка1. Добавим «крылышки» в
- 89. 3117В клетках квадрата переставьте числа так, чтобы
- 90. 35791113151719Решение1. Добавим «крылышки» в средний столбец и
- 91. Даны числа: 5, 10, 15, 20, 25,
- 92. 51015202530354045Решение1. Добавим «крылышки» в средний столбец и
- 93. 107Разместите в свободных клетках квадрата еще числа
- 94. 91011678345Решение1. Добавим «крылышки» в средний столбец и
- 95. ЗадачаСоставить магический квадрат 7×7 одним из способов.
- 96. Как научится строить магические квадраты?Общий метод построения
- 97.
- 98. Магический квадрат 7х7 способом Баше (моя работа)
- 99. Индийский способ построения магического квадрата 5х5 (моя работа)
- 100. Способ поворотов и отражений магического квадрата 3х3 (моя работа) (симметрия относительно диагонали)
- 101. (симметрия относительно оси)
- 102. Доказано, что магических квадратов 5 порядка
- 103. Этот квадрат 8 порядка составлен в 18
- 104. Магический квадрат 9 порядка
- 105. Примеры более сложных квадратов
- 106. Собор Саграда Фамилиа (Святого Семейства) в Барселоне
- 107. Валерий Герловин "Магический квадрат =15" (Magic Square
- 108. В четырехчастном рельефе "Магический квадрат = 15"
- 109. Спасибо за внимание!
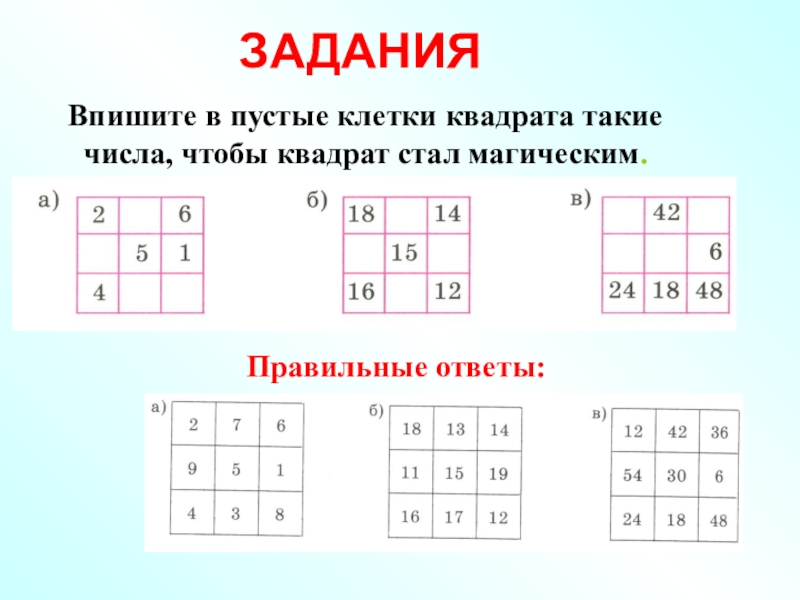
- 110. ЗАДАНИЯ Впишите в пустые клетки квадрата такие числа, чтобы квадрат стал магическим.Правильные ответы:
- 111. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2«Составление магических квадратов, представляет собой превосходную умственную гимнастику, развивающую способность
понимать идеи размещения, сочетания, симметрии, классификации, обобщения и т.д.»
А.
ОбриСлайд 3Цель работы: изучить магические квадраты и его свойства
Задачи:
познакомиться
с историей магических квадратов, выяснить виды магических квадратов и
способы их заполнения;познакомиться с трудами древних ученых;
использовать Интернет для получения информации;
провести исследования не менее десяти различных областей, в которых есть квадрат.
Слайд 4Магическим квадратом n-го порядка называется квадратная таблица размером n х
n, заполненная натуральными числами от 1 до n2, суммы которых
по всем строкам, столбцам и обеим диагоналям одинаковы.Слайд 5Основные понятия
Главная диагональ – проходит через
центр квадрата.
Ломаная диагональ – дойдя до края квадрата, продолжается параллельно
первому отрезку от противоположного края.Различают магические квадраты четного и нечетного порядка (в зависимости oт четности n).
Каждый элемент МК называется клеткой.
Слайд 6Первые значения магических констант приведены
в следующей таблице:
Сумма чисел в каждой
строке, столбце и на диагоналях, называется магической константой, M. Магическая
константа нормального волшебного квадрата зависит только от n и определяется формулой.Магическая константа
Слайд 7История возникновения
магических квадратов
Магический квадрат –древнекитайского происхождения.
Согласно легенде, во время правления императора Ю из вод Хуанхэ
(Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифыСлайд 8Магическим квадратам приписывали различные мистические свойства.
Бытовало поверье, что выгравированный на серебре
магический квадрат
защищает от чумы.
Мистические амулеты
Слайд 9 Квадрат Дюрера «Меланхолия»
Сумма чисел, расположенных по его углам, равна магическому числу 34; суммы чисел в каждом из пяти маленьких квадратов (в четыре клетки), примыкающих к вершинам данного квадрата, и в таком же центральном квадрате тоже равны 34; в каждой его строке есть пара чисел, сумма которых равна 15, и ещё пара рядов стоящих чисел, сумма которых равна 19.
Слайд 10Один из наиболее известных магических квадратов – великий квадрат Сатор.
Заключенный в нем текст - Sator Arepo Tenet Opera Rotas
- одинаково читается по всех четырех направлениях. Латинским перевод слова "Сатор" - сеятель.
Слайд 11Магического квадрата 2-го порядка не существует
Как ни расставляй числа в
клетках таблицы, их сумма будет равна 5 либо в каждой
строке (а), либо в обоих столбцах (б), либо по диагоналям (в), но никак не одновременно.а
в
б
Слайд 12Существует единственный магический квадрат 3*3, так как остальные магические квадраты
3*3 получаются из него либо перестановкой строк (а) или столбцов
(б) либо путем поворота исходного квадрата на 90° (в) или на 180° (г).Слайд 13Латинские квадраты
если один квадрат наложить на другой, то все пары
получившихся чисел оказываются различными. Такие пары латинских квадратов называются ортогональными.
Латинским квадратом называется квадрат n*n клеток, в которых написаны числа 1, 2, 3, .. n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу.
Особенность латинских квадратов:
Слайд 14Старинная занимательная задача Эйлера:
«Среди 36 офицеров поровну уланов, драгунов,
гусаров, кирасиров, кавалергардов и гренадеров. кроме того, поровну генералов, полковников,
майоров, капитанов, поручиков и подпоручиков, причем каждый род войск представлен офицерами всех шести рангов. Можно ли выстроить этих офицеров в каре 6х6 так, чтобы в любой колонне и любой шеренге встречались офицеры всех рангов?»Эйлер не смог найти решения этой задачи. В 1901 г. было доказано, что такого решения не существует. В то же время Эйлер доказал, что для 25 офицеров решение есть. На рисунке показано, что чин офицера символизирует цветной кружок в углу каждой из клеток
Слайд 15 Дьявольский магический квадрат — магический квадрат, в котором также с
магической константой совпадают суммы чисел по ломаным диагоналям в обоих
направлениях. Такие квадраты называются ещё пандиагональными.
Дьявольский магический квадрат
Слайд 16Древнейший из дошедших до нас квадратов четвертого порядка был обнаружен
в надписи XI или XII века, найденной в Кхаджурахо (Индия).
Слайд 17Квадраты, у которых суммы чисел, расположенные на «разломанных» диагоналях, равны
постоянной магического квадрата.
Постоянная равна 65
Совершенные квадраты.
Если из одинаковых дьявольских квадратов
выложить мозаику (каждый квадрат должен вплотную примыкать к своим соседям) то получится нечто вроде паркета, в котором числа стоящие в любой группе клеток 4х4 будут образовывать дьявольский квадрат. Слайд 18
Если пандиагональный квадрат еще и ассоциативный, то он носит название
идеальный. Пример идеального магического квадрата:
Идеальный квадрат
Слайд 19Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые
их называют совершенными.
Совершенных квадратов нечётного порядка не существует
Среди пандиагональных квадратов
двойной чётностивыше 4 имеются совершенные.
Разломанные диагонали
пандиагонального
квадрата.
Слайд 20Квадрат, в котором любые два числа, расположенные симметрично относительно его
центра, дают в сумме одно и то же число, называется
симметрическим.Слайд 21 Бенджамин Франклин составил квадрат 16×16
который помимо наличия постоянной суммы 2056 во всех строках, столбцах
и диагоналях имел еще одно дополнительное свойство. Если вырезать из листа бумаги квадрат 4×4 и уложить этот лист на большой квадрат так, чтобы 16 клеток большего квадрата попали в эту прорезь, то сумма чисел, появившихся в этой прорези, куда бы мы ее не положили, будет одна и та же – 2056.Магический квадрат 16*16
Слайд 26Магические квадраты и
«магия планет»
Каждой планете соответствует свой числовой магический квадрат,
с помощью которого можно привлечь силу этой планеты. Например, квадраты
Сатурна и Юпитера таковы:Квадрат Сатурна — древнейший из известных магических квадратов: он приводится уже в китайской «Книге Перемен». Он состоит из трех строк, каждая из которых содержит по три числа, так как Сатурн соответствует третьей сефире.
А квадрат Юпитера, соответствующего четвертой сефире, содержит четыре строки по четыре числа в каждой.
Юпитер
Сатурн
Слайд 27Магические квадраты и
«магия планет»
В квадрате Солнца — шесть строк, содержащих по
шесть чисел, от 1 до 36, а если суммировать все
числа, входящие в этот квадрат, то получится 666.На Основании этого маги пришли к выводу, что Зверь из Книги Откровения — это одна из ипостасей Солнца, или жизненной силы.
Это буйная, дикая, безудержно бьющая через край энергия, благодаря которой все живое стремится выжить, продолжить свой род и подчинить себе окружающую среду.
Всего чисел 36
Сумма в каждой строке, столбце и по диагоналям=111
Слайд 31 Судо́ку — это головоломка-пазл с числами, ставшая
в последнее время очень популярной. В переводе с японского «су» —
«цифра», «доку» — «стоящая отдельно». Иногда судоку называют «магическим квадратом», что в общем-то не верно, так как судоку является латинским квадратом 9-го порядка.Слайд 34 Фэн шуй – это древнекитайское искусство, которое рассматривает человека и
все, что его окружает, как единую структуру и стремится привести
эту структуру к максимальной гармонии.Цель фэн-шуй: поиск благоприятных потоков энергии ци и её использование на благо человека.
Фэн-шуй
Слайд 35Тайный сад. Феншуй.
Тайный сад - это тихая, достаточно уединенная
часть сада, где Вы можете расслабиться и забыть о повседневных
заботах. В идеальном случае это место, где Вас никто не побеспокоит. Это нечто вроде пещеры отшельника, где Вы можете отдаться единению с природой и успокоить душу. Все триграммы расположены согласно «магическому квадрату»Магический квадрат
Слайд 37 Цифры, стоящие в клетках рисунка, означают: первая - количество килограммов
удобрения первого вида, вносимого на участок, а вторая - количество
вносимогоудобрения второго вида.Использование ортогональных латинских квадратов помогает учесть все возможные варианты в экспериментах в сельском хозяйстве, физике, химии, технике.
Слайд 38Старинная занимательная задача Эйлера:
«Среди 36 офицеров поровну уланов, драгунов,
гусаров, кирасиров, кавалергардов и гренадеров. кроме того, поровну генералов, полковников,
майоров, капитанов, поручиков и подпоручиков, причем каждый род войск представлен офицерами всех шести рангов. Можно ли выстроить этих офицеров в каре 6х6 так, чтобы в любой колонне и любой шеренге встречались офицеры всех рангов?»Эйлер не смог найти решения этой задачи. В 1901 г. было доказано, что такого решения не существует. В то же время Эйлер доказал, что для 25 офицеров решение есть. На рисунке показано, что чин офицера символизирует цветной кружок в углу каждой из клеток
Слайд 43Моя дата рождения 13.04.1995
1)Сложим цифры даты рождения:
1+3+4+9+9+5=31.
2) Складываем цифры
результата: 3+1=4.
3) Из первой суммы вычитаем удвоенную первую цифру
дня рождения: 31-8=23.
4) Складываем цифры результата: 2+3=5.
5) Складываем 1 и 3, 2 и 4 суммы:
31+23=54, 4+5=9.
Получили числа
13.04.1995,31,4,23, 5, 54,9.
Составляем магический квадрат
Слайд 44Клетки имеют следующие значения:
1. Характер человека, эго, воля, осознание.
2. Биоэнергетика. Энергия Солнца.
3. Внутренний склад человека,
хозяйственность, порядочность. 4. Здоровье.
5. Интуиция.
6. Способности биоэнергетической части данной личности накапливать и
преобразовывать энергию Земли, необходимую для созидательной или разрушительной деятельности.
7. Талантливость данной личности.
8. Возможное чувство долга, способность человека стремиться к свободе и ощущать себя ответственным за свои обязательства, стремление к завершению начатых им дел.
9. Количество девяток влияет на процессы развития и использования таланта.
Слайд 45Значение ячеек квадрата
ЯЧЕЙКА 1 – целеустремлённость, воля, упорство, эгоизм.
1
– законченные эгоисты, стремятся из любого положения извлечь максимальную
выгоду.11 – характер близкий к эгоистическому.
111 – «золотая середина».Характер спокойный, покладистый, коммуникабельный.
1111 – люди сильного характера, волевые. Мужчины с таким характером подходят на роль военных-профессионалов, а женщины держат свою семью в кулаке.
11111 – диктатор, самодур.
111111 - человек жестокий, способный совершить невозможное; нередко попадает под влияние какой-то идеи.
ЯЧЕЙКА 2 – биоэнергетика, эмоциональность, душевность, чувственность. Количество двоек определяет уровень биоэнергетики.
2 – обычные в биоэнергетическом отношении люди. Такие люди очень чувствительны к изменениям в атмосфере.
22 – относительно большой запас биоэнергетики. Из таких людей получаются хорошие врачи. В семье таких людей редко у кого бывают нервные стрессы.
222 – знак экстрасенса.
ЯЧЕЙКА 3 – точность, конкретность, организованность, аккуратность, пунктуальность, чистоплотность, скупость, наклонность к постоянному « восстановлению справедливости». Нарастание троек усиливает все эти качества. С ними человеку есть смысл искать себя в науках, особенно точных.
Слайд 46ЯЧЕЙКА 4 – здоровье. Это связаноэкгрегором, то есть энергетическим пространством,
наработанным предками и защищающим человека. Отсутствие четвёрок свидетельствует о болезни
человека.4 – здоровье среднее, необходимо закалять организм. Из видов спорта рекомендуются плавание и бег.
44 – здоровье крепкое,
444 и более – люди с очень крепким здоровьем.
ЯЧЕЙКА 5 – интуиция, ясновиденье начинающееся проявляться у таких людей уже на уровне трёх пятерок. Пятерок нет-канал связи с космосом закрыт. Эти люди часто ошибаются.
5 – канал связи открыт. Эти люди могут правильно рассчитать ситуацию извлечь из неё максимальную пользу.
55 – сильно развита интуиция. Когда видят « вещие сны», могут предугадать ход событий. Подходящие для них профессии-юрист, следователь.
555 – почти ясновидящие.
5555 – ясновидящие.
ЯЧЕЙКА 6 – заземлённость, материальность, расчёт, склонность к количественному освоению мира и недоверие к качественным скачкам и тем более к чудесам духовного порядка.
6 – могут заниматься творчеством или точными науками, но физический труд является обязательным условием существования.
66 – заземлённые люди, тянуться к физическому труду, хотя как раз для них он не обязателен, желательна умственная деятельность либо занятия искусством.
666 – знак Сатаны, особый и зловещий знак. Эти люди обладают повышенным темпераментом, обаятельны, неизменно становятся в обществе центром внимания.
6666 – эти люди в своих предыдущих воплощениях набрали слишком много заземлённости, они очень много трудились и не представляют свою жизнь без труда.
Слайд 47ЯЧЕЙКА 7 – мера таланта.
7 – чем больше они
работают, тем больше получают в последствии.
77 – очень одарённые,
музыкальные люди, тонкий художественный вкус.777 – эти люди, как правило, приходят на землю ненадолго. Они добры, безмятежны, чувствительны, любят мечтать, не всегда чувствуют реальность.
7777 – знак Ангела, Люди с таким знаком умирают в младенчестве, а если живут, то их жизни постоянно угрожает опасность.
ЯЧЕЙКА 8 – карма, долг, обязанность, ответственность.
8 – натуры ответственные, добросовестные, точные.
88 – у этих людей развитое чувство долга, их отличает желание помочь другим.
888 – знак великого долга, служения народу. Правитель с тремя 8-ми добивается выдающихся результатов.
8888 – парапсихологические способности и исключительная восприимчивость к точным наукам.
ЯЧЕЙКА 9 – ум, мудрость. Отсутствие девяток – свидетельство того, что умственные способности крайне ограничены.
9 – эти люди должны всю жизнь трудиться, чтобы восполнить недостаток ума.
99– эти люди умны от рождения. Учатся всегда неохотно, потому что знания даются им легко. Они наделены чувством юмора с ироничным оттенком, независимые.
999 – очень умны. К учению вообще не прикладывают никаких усилий. Прекрасные собеседники.
9999 – этим людям открывается истина. Если у них к тому же развита интуиция, то они гарантированы от провала в любом из своих начинаний. При всём этом они, как правило, довольно приятны, так как острый ум делает их грубыми, немилосердными, жестокими.
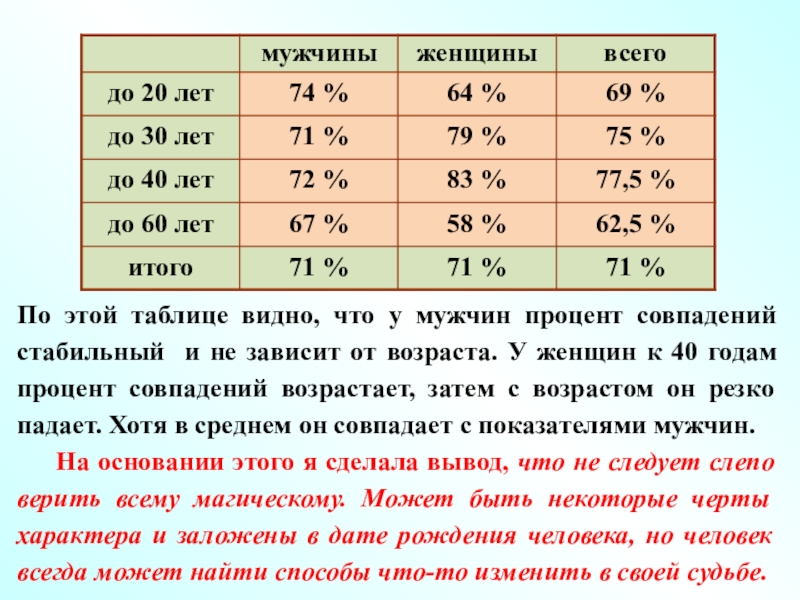
Слайд 48По этой таблице видно, что у мужчин процент совпадений
стабильный и не зависит от возраста. У женщин к 40
годам процент совпадений возрастает, затем с возрастом он резко падает. Хотя в среднем он совпадает с показателями мужчин.На основании этого я сделала вывод, что не следует слепо верить всему магическому. Может быть некоторые черты характера и заложены в дате рождения человека, но человек всегда может найти способы что-то изменить в своей судьбе.
Слайд 531
2
3
4
5
6
7
8
9
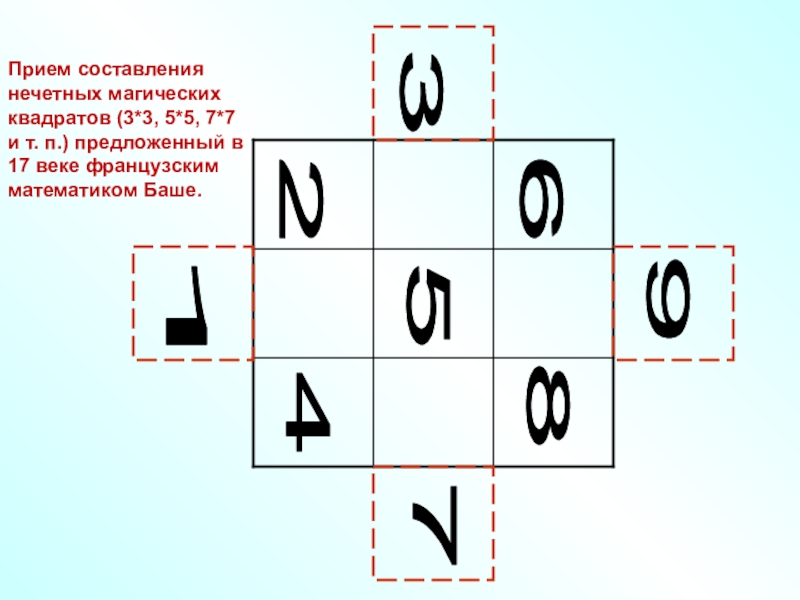
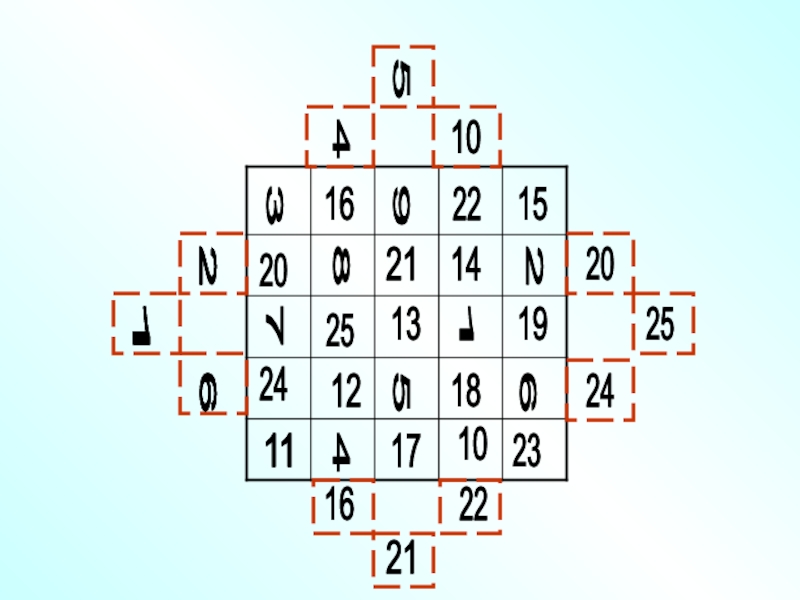
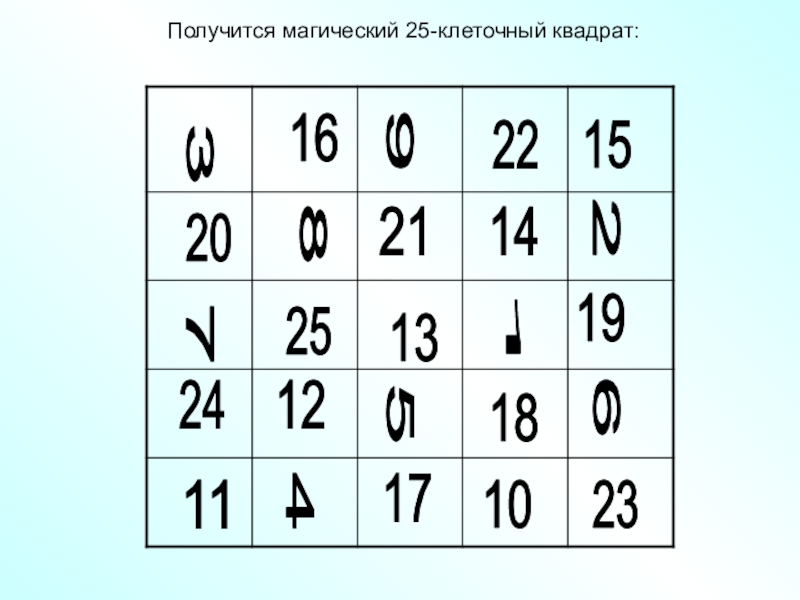
Прием составления нечетных магических квадратов (3*3, 5*5, 7*7 и т.
п.) предложенный в 17 веке французским математиком Баше.
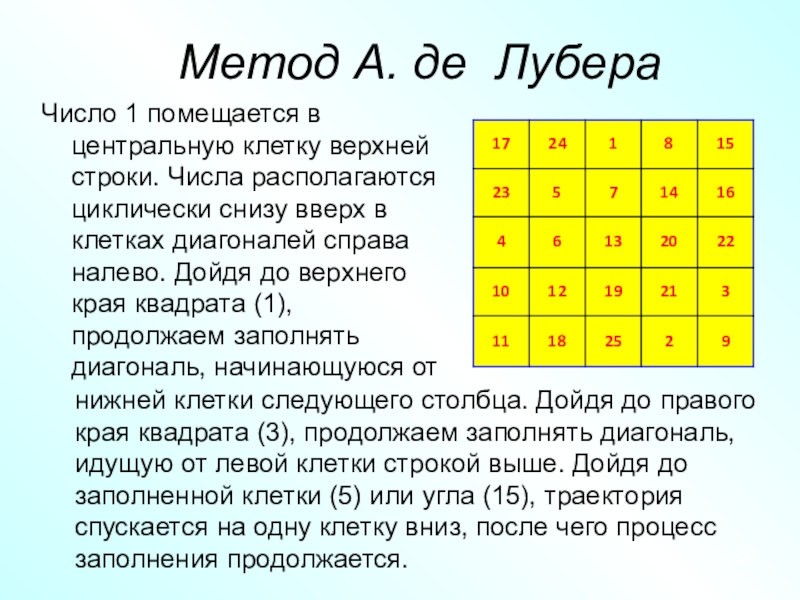
Слайд 56Метод А. де Лубера
Число 1 помещается в центральную клетку верхней
строки. Числа располагаются циклически снизу вверх в клетках диагоналей справа
налево. Дойдя до верхнего края квадрата (1), продолжаем заполнять диагональ, начинающуюся отнижней клетки следующего столбца. Дойдя до правого края квадрата (3), продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки (5) или угла (15), траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.
Слайд 59
Магические квадраты нечетного порядка
Метод достроения
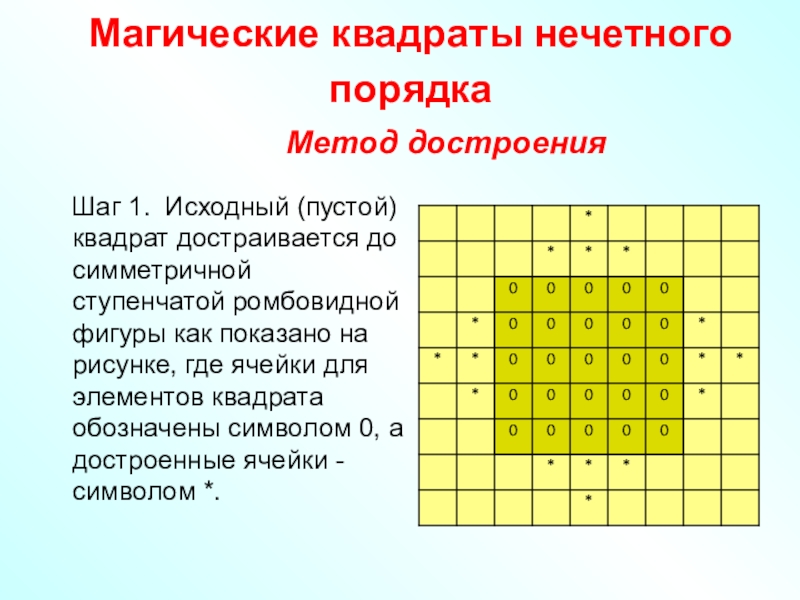
Шаг 1. Исходный (пустой) квадрат достраивается до симметричной ступенчатой ромбовидной
фигуры как показано на рисунке, где ячейки для элементов квадрата обозначены символом 0, а достроенные ячейки - символом *.Слайд 60Метод достроения
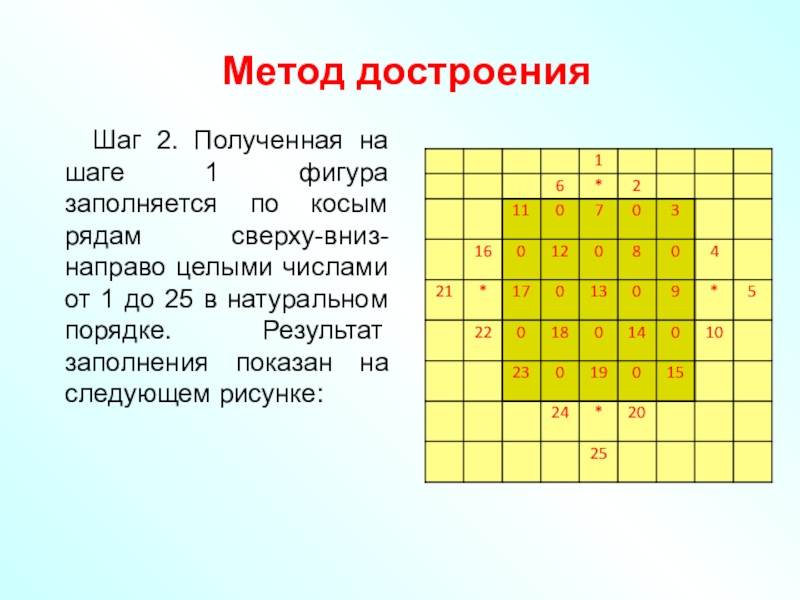
Шаг 2. Полученная на шаге 1 фигура
заполняется по косым рядам сверху-вниз-направо целыми числами от 1 до
25 в натуральном порядке. Результат заполнения показан на следующем рисунке:Слайд 61Метод достроения
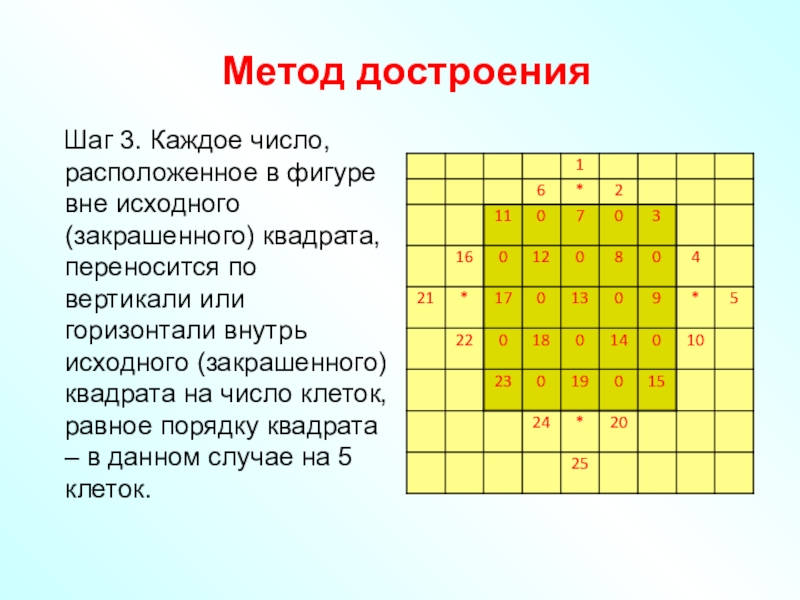
Шаг 3. Каждое число, расположенное в фигуре
вне исходного (закрашенного) квадрата, переносится по вертикали или горизонтали внутрь
исходного (закрашенного) квадрата на число клеток, равное порядку квадрата – в данном случае на 5 клеток.Слайд 62В левом верхнем квадрате порядка 5 выделить 3 группы клеток,
пометив их знаками + (голубой цвет), - (желтый цвет) и
* (розовый цвет) соответственно. В каждой строке и каждом столбце нужно выделить по 2 [10=2*5=2*(2*2+1)] клетки первой группы. Их можно расставить по главной диагонали и на ломаной1 диагонали. Клеток второго и третьего типа надо выделить по одной в каждой строке и каждом столбце. В качестве клеток второй и третьей групп можно взять клетки, расположенные на двух других ломаных диагоналях.Диагональный метод.
Слайд 63Метод достроения
Шаг 4. Освободившиеся ячейки, заполненные
символом *, должны быть
исключены.
Оставшиеся внутренние ячейки, заполненные натуральными числами,
образуют магический квадрат,
представленный следующей таблицей 5x5: Сумма чисел в столбцах, строках, диагоналях
равна 65.
Слайд 64Квадраты нечетного порядка
Строим, квадрат ABCD с 25 клетками и временно
дополняем его до, симметричной ступенчатой фигуры со ступеньками в одну
клетку.В полученной фигуре располагаем по порядку косыми рядами сверху вниз - направо 25 целых чисел от 1до 25.
А теперь каждое число, оказавшееся вне квадрата ABCD, следует перенести вдоль того же ряда или столбца ровно на столько клеток от той клетки, которую оно занимает, каков порядок квадрата, в нашем примере - на пять. Так, в соответствии с этим правилом переносим эти числа…
15
2
19
6
23
22
14
1
18
10
9
21
13
5
17
16
8
25
12
4
3
20
7
24
11
A
B
C
D
Слайд 65Четно – нечетные квадраты
Диагональный метод
Получится четно-нечетный магический квадрат с
суммой, равной 505.
Слайд 66Построение магических квадратов
Метод террас
Для заданного нечетного N начертим квадратную таблицу
размером NxN. Пристроим к этой таблице со всех четырех сторон
террасы (пирамидки). В результате получим ступенчатую симметричную фигуру. Начиная с левой вершины ступенчатой фигуры, заполним ее диагональные ряды последовательными натуральными числами от 1 до N².После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером NxN, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.
Слайд 67Метод А.де ла Лубера (французского геометра 17 в.)
Число 1 помещается
в центральную клетку верхней строки. Все натуральные числа располагаются в
естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата (как в случае числа 1), продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца. Дойдя до правого края квадрата (число 3), продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки (число 5) или угла (число 15), траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.Сумма чисел в столбцах, строках, диагоналях равна 65.
Слайд 68Известно, что шахматы, как и магические квадраты, появились десятки веков
назад в Индии. Поэтому неслучайно возникла идея шахматного подхода к
построению магических квадратов.Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы.
Шахматный подход
Слайд 69 Шахматная разбивка позволяет создавать любой магический квадрат.
Цифры заполняются
регулярно и построчно с учётом цвета ячеек.
Схема построения магических квадратов
Слайд 70Построение магического квадрата 7-го порядка универсальным способом
Строим квадрат размером
5×5 клеток и дополняем его до, симметричной фигуры – ромба.
В полученной фигуре располагаем числа от 1 до 25 по порядку косыми рядами сверху вниз
А теперь каждое число, оказавшееся вне квадрата, перенесём вдоль того же ряда или столбца ровно на 5 клеток и заполним пустые места.
15
2
19
6
23
22
14
1
18
10
9
21
13
5
17
16
8
25
12
4
3
20
7
24
11
Слайд 73Квадрат Ло-Шу
Ло Шу (кит. трад. 洛書, упр. 洛书, пиньинь: luò
shū) Единственный нормальный магический квадрат 3×3. Был известен ещё в
Древнем Китае, первое изображение на черепаховом панцире датируется 2200г. до н.э.Слайд 74В XIII в. математик Ян Хуэй занялся проблемой методов построения
магических квадратов, не только третьего, но и больших порядков.
Он
сумел построить магический квадрат шестого порядкаМагический квадрат Ян Хуэя
(Китай)
Слайд 75Квадрат, найденный в Кхаджурахо (Индия)
Самый ранний уникальный магический квадрат обнаружен
в надписи XI века в индийском городе Кхаджурахо:
Слайд 76Магический квадрат
Ян Хуэя (Китай)
В 13 в. математик Ян Хуэй
занялся проблемой методов построения магических квадратов. Его исследования были потом
продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37)Слайд 77Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.
Если в квадратную
матрицу n × n заносится не строго натуральный ряд чисел,
то данный магический квадрат — нетрадиционный. Ниже представлены два таких магических квадрата, заполненные в основном простыми числами. Первый имеет порядок n=3 (квадрат Дьюдени); второй (размером 4x4) — квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия:Слайд 78Квадрат Альбрехта Дюрера
Фрагмент гравюры Дюрера «Меланхолия»
Магический квадрат 4×4, изображённый на
гравюре Альбрехта Дюрера «Меланхолия I», считается самым ранним в европейском
искусстве.[5] Два средних числа в нижнем ряду указывают дату создания картины (1514).Слайд 79Магический квадрат Эйлера
Этот квадрат 8 порядка составлен в 18 веке
великим Леонардом Эйлером. Каждый ряд в этом квадрате даёт сумму
260, половина ряда– 130.Слайд 80Квадрат Багуа
Магический квадрат в фэн-шуй — основа расположения предметов
в пространстве. Имеет этот квадрат девять секторов. Каждый из секторов
отвечает за различные стороны нашей жизни. Этот квадрат у китайцев означает «Поле чудес», на их сленге - багуа. «Багуа» - квадрат, делящийся на девять частей, каждая несет свою информацию:
1 - карьера
2 - партнёрство
3 - семья
4 - богатство
5 - центр (сила)
6 - помощники
7 - дети
8 - знания
9 - слава (мудрость)
Слайд 81Квадрат Джона Манси
17 век
Составлен из 143 последовательных простых чисел (исключением
является число 1 и число 2)
Слайд 82Просто КВАДРАТ и
никаких фокусов.
Предположительно слово «Абракадабра» произошло от халдейского
выражения ab bada ke
daabra, что означало сгинь, как огонь». Есть
ещё одна версия происхождения этогомагического слова – от имени божественного года Абракаса, число которого составляет 365.
Именно это божество должно было принести человеку здоровье и целостность
Слайд 86Трудные задачи
Простым числам было посвящено множество занимательных математических задач. Одна
из них была придумана Генри Эрнестом Дьюдни, известным английским специалистом
по головоломкам. Существуют ли магические квадраты, состоящие только из простых чисел?Оказывается, да. Магический квадрат размером 3х3, имеет сумму 111 (между прочим, тоже не простое число) вдоль каждой строки, каждого столбца и каждой главной диагонали.
Я составила лишь не полный магический квадрат 3х3 из простых чисел (потратил на это 3 часа, заодно поупражнялся в устном счете):
Слайд 87Квадрат разделен на 9 равных клеток. Расставьте в этих клетках
числа 1, 2, 3, 4, 5, 6, 7, 8, 9
так, чтобы сумма чисел в каждой строке и в каждом столбике равнялась 15.Магический квадрат 1
Слайд 881
2
3
4
5
6
7
8
9
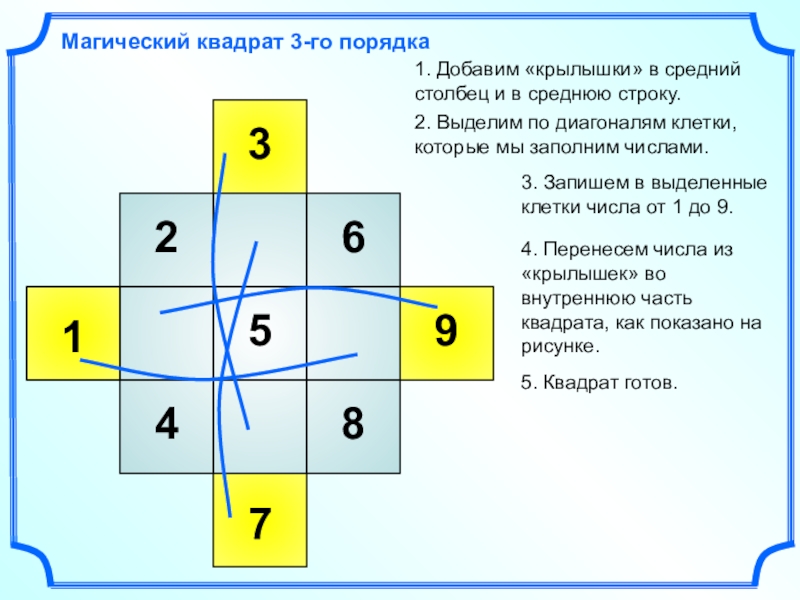
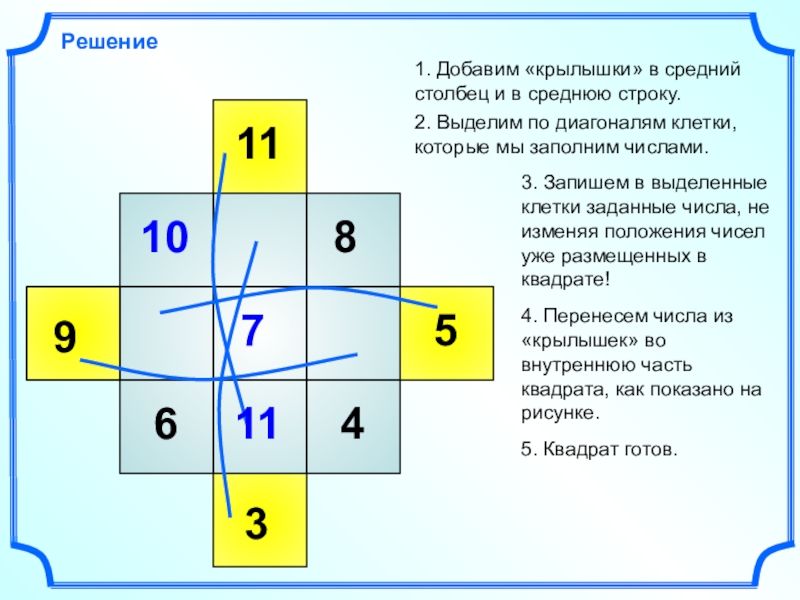
Магический квадрат 3-го порядка
1. Добавим «крылышки» в средний столбец и
в среднюю строку.
2. Выделим по диагоналям клетки, которые мы заполним
числами.3. Запишем в выделенные клетки числа от 1 до 9.
4. Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.
5. Квадрат готов.
Слайд 893
11
7
В клетках квадрата переставьте числа так, чтобы по любой вертикали,
горизонтали и диагонали их суммы были равны между собой:
Заполним
квадрат числами 3, 5, 7, 9, 11, 13, 15, 17 и 19по описанному алгоритму.
5
9
13
17
19
15
Магический квадрат 2
Слайд 903
5
7
9
11
13
15
17
19
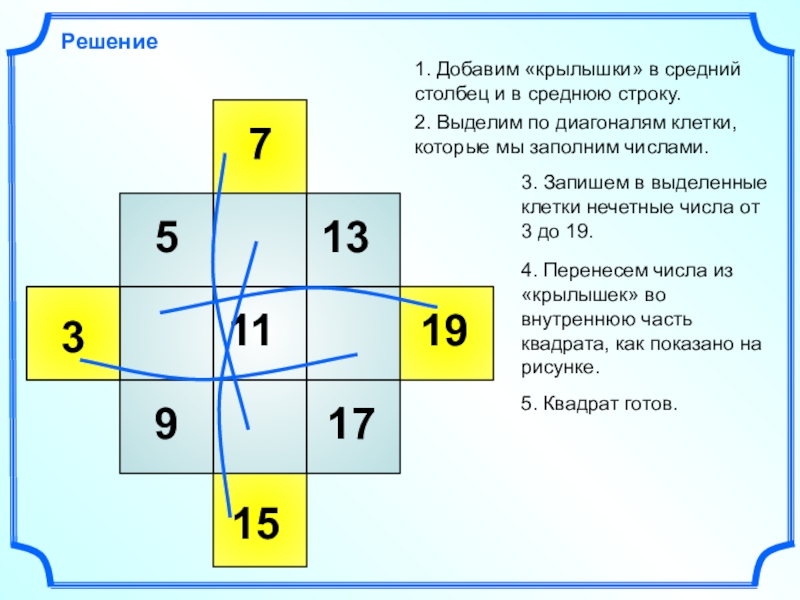
Решение
1. Добавим «крылышки» в средний столбец и в среднюю строку.
2.
Выделим по диагоналям клетки, которые мы заполним числами.
3. Запишем в
выделенные клетки нечетные числа от 3 до 19.4. Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.
5. Квадрат готов.
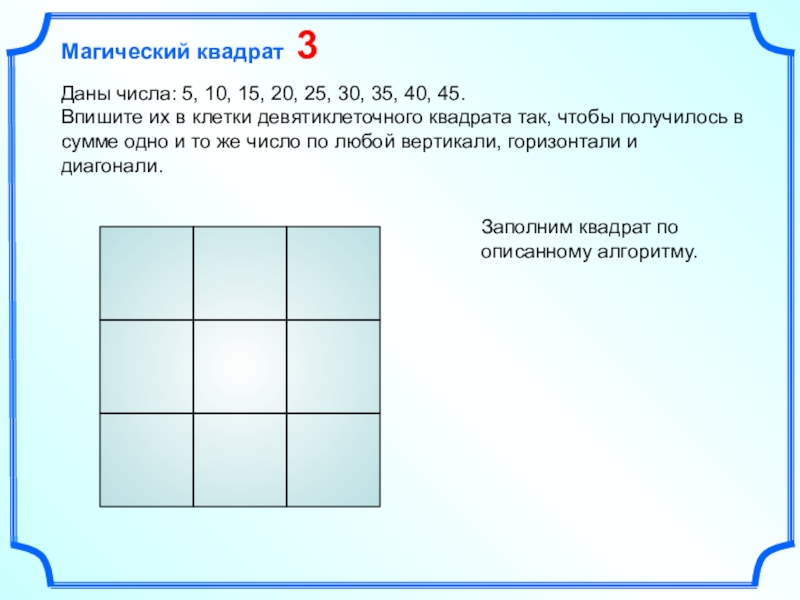
Слайд 91Даны числа: 5, 10, 15, 20, 25, 30, 35, 40,
45.
Впишите их в клетки девятиклеточного квадрата так, чтобы получилось в
сумме одно и то же число по любой вертикали, горизонтали и диагонали.Заполним квадрат по описанному алгоритму.
Магический квадрат 3
Слайд 925
10
15
20
25
30
35
40
45
Решение
1. Добавим «крылышки» в средний столбец и в среднюю строку.
2.
Выделим по диагоналям клетки, которые мы заполним числами.
3. Запишем в
выделенные клетки заданные числа.4. Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.
5. Квадрат готов.
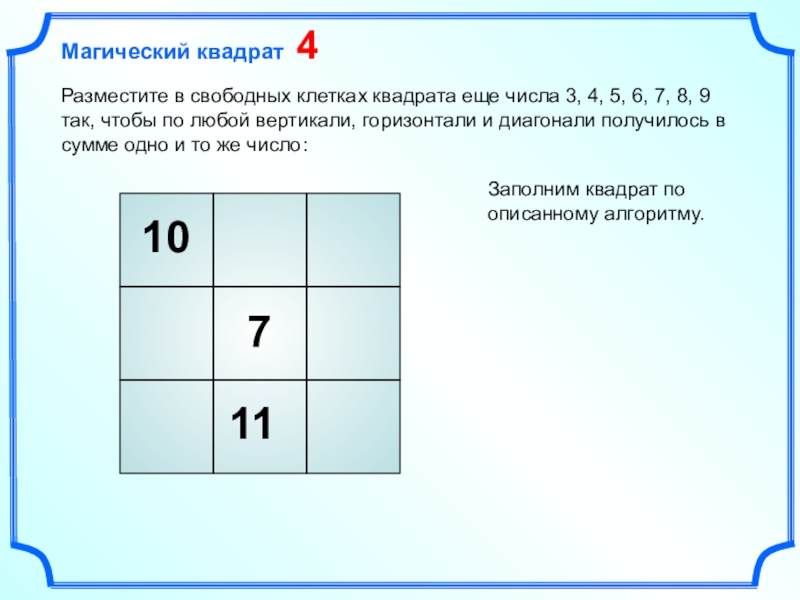
Слайд 9310
7
Разместите в свободных клетках квадрата еще числа 3, 4, 5,
6, 7, 8, 9 так, чтобы по любой вертикали, горизонтали
и диагонали получилось в сумме одно и то же число:Заполним квадрат по описанному алгоритму.
11
Магический квадрат 4
Слайд 949
10
11
6
7
8
3
4
5
Решение
1. Добавим «крылышки» в средний столбец и в среднюю строку.
2.
Выделим по диагоналям клетки, которые мы заполним числами.
3. Запишем в
выделенные клетки заданные числа, не изменяя положения чисел уже размещенных в квадрате! 4. Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунке.
5. Квадрат готов.
11
Слайд 95Задача
Составить магический квадрат 7×7 одним из способов. Я использовала способ
Клода Баше де Мезириака.
Диагональный квадрат
Составленный магический квадрат
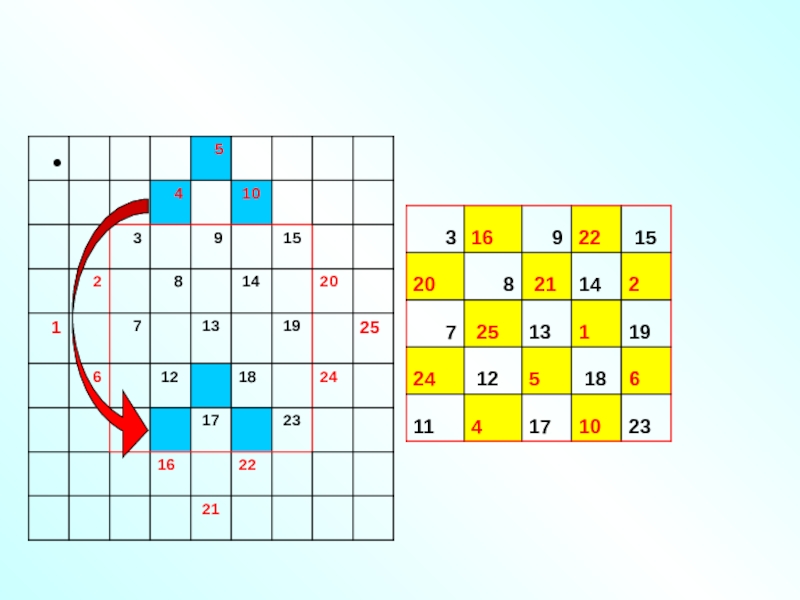
Слайд 96Как научится строить магические квадраты?
Общий метод построения всех квадратов неизвестен,
хотя широко применяются различные схемы.
Вот один метод:
Пусть
n – нечетное число, и нужно построить квадрат nxn С числами от 1 до n². Действуем поэтапно. Все числа от 1 до n² записываем в клеточки по диагонали, чтобы образовался диагональный квадрат.
Выделяем в его центре квадрат nxn. Это и есть основа будущего квадрата.
Каждый находящийся вне центрального числовой угол аккуратно переносим внутрь- к противоположной стороне квадрата. Числа этих уголков должны заполнить все пустые клетки
Слайд 100Способ поворотов и отражений магического квадрата 3х3 (моя работа) (симметрия относительно
диагонали)
Слайд 103Этот квадрат 8 порядка составлен в 18 в
великим
Леонардом Эйлером. Каждый ряд в этом квадрате даёт сумму 260,
а половина ряда – 130.Магический квадрат 8 порядка
Слайд 106Собор Саграда Фамилиа (Святого Семейства) в Барселоне
Фасад смерти.
Изображен магический
квадрат. В сумме числа в любой строке, столбце и по
диагонали дают 33.Грандиозное творение великого испанского архитектора, Антонио Гауди (1852- 1926). Собор состоит из трех фасадов: фасад Рождения, Славы и Смерти.