Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные способы решения задач на смеси, сплавы , растворы
Содержание
- 1. Различные способы решения задач на смеси, сплавы , растворы
- 2. Проблема и гипотезаРассматривая учебники по математике разных
- 3. Цели и задачиСистематизировать задачи на растворы, смеси
- 4. ЕГЭ и межпредметная связьСозданный мною проект содержит
- 5. Анализ ситуацииВ ходе проектной деятельности я проводила
- 6. Введение Для решения задач на концентрации
- 7. Основные понятия«Смесь»«Чистое вещество»«Примесь»Доли чистого вещества в смеси
- 8. Классификация задачНа понижение и повышение концентрацииНа «высушивание»На смешивание растворов разных концентраций На переливание
- 9. Задачи на понижение и повышение концентрации
- 10. Решение задачи №1II. Правило «креста»18
- 11. Задачи на высушиваниеЗадача №3:
- 12. Решение задачи №3При решении таких задач надо
- 13. Задачи, которые решаются с помощью систем линейных
- 14. Решение задачи №4Пусть процентное содержание соли в
- 15. Старинная схема решения подобных задачСмешивая 5% и
- 16. Задачи на переливание При решении этих
- 17. Теперь покажу, как графические иллюстрации к условию
- 18. Задача №5 Сначала приготовили 25%-ый водный
- 19. Решение задачи №5До выпаривания:После выпаривания: 25%
- 20. Задача №6 Имеется два сплава золота
- 21. Решение задачи №6I СПЛАВЗолота в нём 0,1
- 22. Внесём данные в таблицу:Имеется два сплава золота
- 23. Вывод При решении задач следует руководствоваться
- 24. ВыводВ ходе проектной деятельности я разделила задачи
- 25. Повторный опрос «Можете ли вы решать задачи на растворы?»53610ДО:Конечно!Скорее всегоЗатруднились ответить НетПОСЛЕ:1491Да!Скорее всегоЗатруднились ответить
- 26. РефлексияКак видно из результатов опросов, проектная деятельность
- 27. Список литературыМ.В. Лурье и др. Задачи на
- 28. Интернет-ресурсы1. Открытый банк заданий ЕГЭ по математике http://www.mathege.ru 2. Шабон оформления презентацииhttp://www.pedsovet.su
- 29. Скачать презентанцию
Проблема и гипотезаРассматривая учебники по математике разных авторов, я увидела несколько совершенно разных по типу задач на растворы, а решения одних и тех же задач в одних учебниках были совершенно
Слайды и текст этой презентации
Слайд 1Различные способы решения задач на смеси, сплавы, растворы
Вайланд Анна Павловна,
учитель математики МАОУ «Средняя общеобразовательная школа №3»
2
Слайд 2Проблема и гипотеза
Рассматривая учебники по математике разных
авторов, я увидела
несколько совершенно разных по типу задач на растворы, а решения
одних и тех же задач в одних учебниках были совершенно другими, нежели в других. Поэтому выдвинула свою гипотезу:Гипотеза: все задачи на растворы, сплавы и смеси делятся на несколько типов, а каждый из типов имеет конкретный способ решения.
Слайд 3Цели и задачи
Систематизировать задачи на растворы, смеси и сплавы;
Найти единый
алгоритм решения этих задач;
Научиться решать задачи по заданной теме.
Слайд 4ЕГЭ и межпредметная связь
Созданный мною проект содержит материал по теме
«Проценты» из курса математики, который может помочь также и при
решении заданий на проценты не только в тестах ЕГЭ по математике за курс основной и средней школы, а так же при изучении химии, биологии, физики и других предметов.
Слайд 5Анализ ситуации
В ходе проектной деятельности я проводила опрос «Можете ли
вы решать задачи на растворы?».
Вот результаты первого:
Конечно!
Скорее всего
Затруднились ответить
Нет
5
3
6
10
Слайд 6Введение
Для решения задач на концентрации нужно уметь рассуждать
и решать задачи на дроби и проценты, на составление уравнений
и их систем. Эти задачи решаются арифметически, применением линейного уравнения и их систем, и другие способы.
Слайд 7Основные понятия
«Смесь»
«Чистое вещество»
«Примесь»
Доли чистого вещества в смеси – «a»
Чистое вещество
– «m»
Общее количество – «М»
a = m :
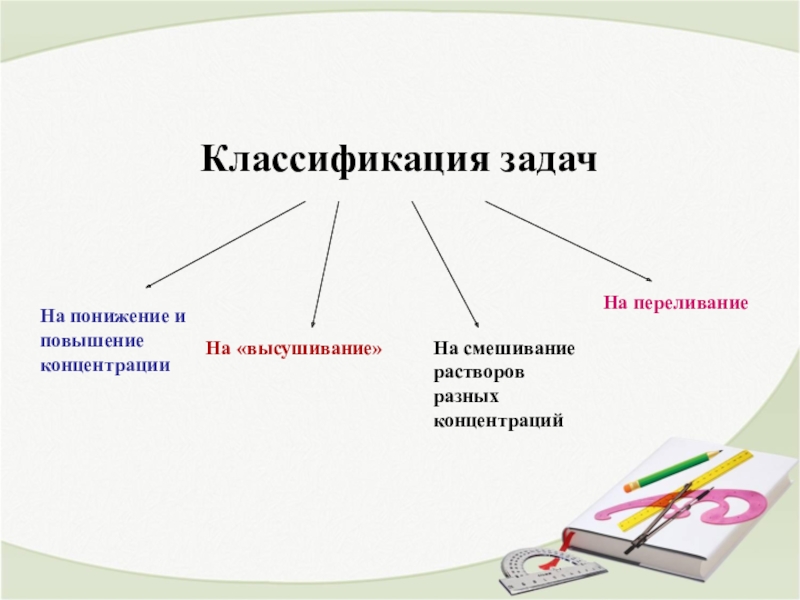
M m = a M M= m : a
Слайд 8Классификация задач
На понижение и повышение концентрации
На «высушивание»
На смешивание растворов разных
концентраций
На переливание
Слайд 9Задачи на понижение и повышение концентрации
Задача №1: сироп
содержит 18% сахара. Сколько кг воды нужно добавить к 40
кг сиропа, чтобы содержание сахара составило 15% ?Задача №2: сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди?
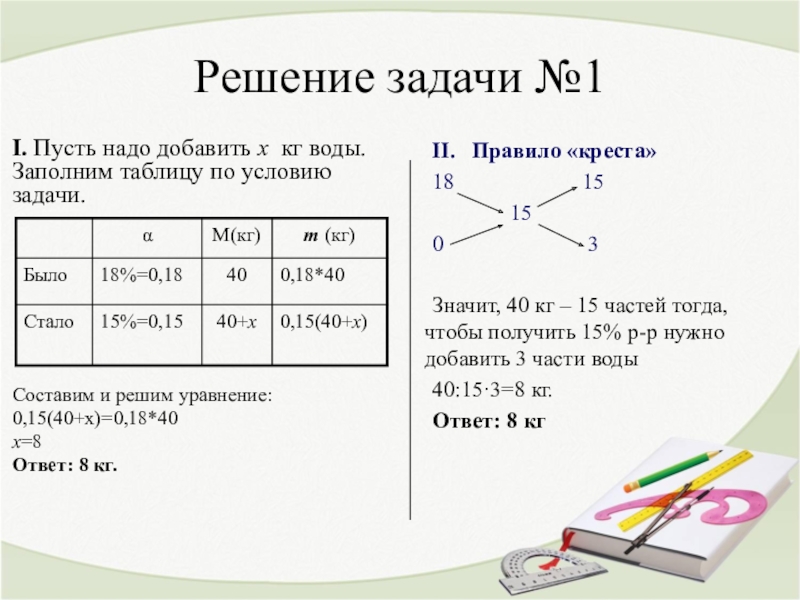
Слайд 10Решение задачи №1
II. Правило «креста»
18
15
150 3
Значит, 40 кг – 15 частей тогда, чтобы получить 15% р-р нужно добавить 3 части воды
40:15·3=8 кг.
Ответ: 8 кг
I. Пусть надо добавить х кг воды. Заполним таблицу по условию задачи.
Составим и решим уравнение:
0,15(40+х)=0,18*40
х=8
Ответ: 8 кг.
Слайд 11Задачи на высушивание
Задача №3:
Пчелы перерабатывают цветочный
нектар в мёд, освобождая его от воды. Нектар содержит 84%
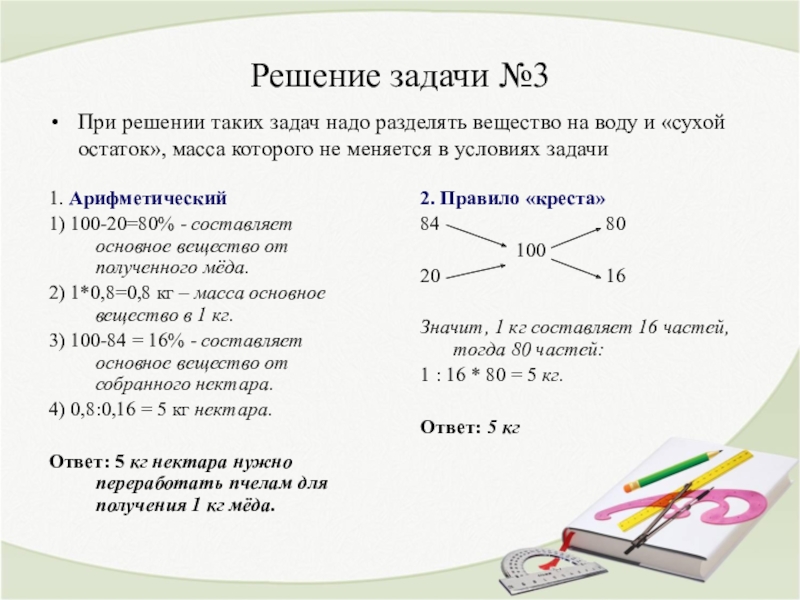
воды, а полученный мёд - 20%. Сколько кг нектара нужно переработать пчелам для получения 1 кг мёда?
Слайд 12Решение задачи №3
При решении таких задач надо разделять вещество на
воду и «сухой остаток», масса которого не меняется в условиях
задачи1. Арифметический
1) 100-20=80% - составляет основное вещество от полученного мёда.
2) 1*0,8=0,8 кг – масса основное вещество в 1 кг.
3) 100-84 = 16% - составляет основное вещество от собранного нектара.
4) 0,8:0,16 = 5 кг нектара.
Ответ: 5 кг нектара нужно переработать пчелам для получения 1 кг мёда.
2. Правило «креста»
84 80
100
20 16
Значит, 1 кг составляет 16 частей, тогда 80 частей:
1 : 16 * 80 = 5 кг.
Ответ: 5 кг
Слайд 13Задачи, которые решаются с помощью
систем линейных уравнений.
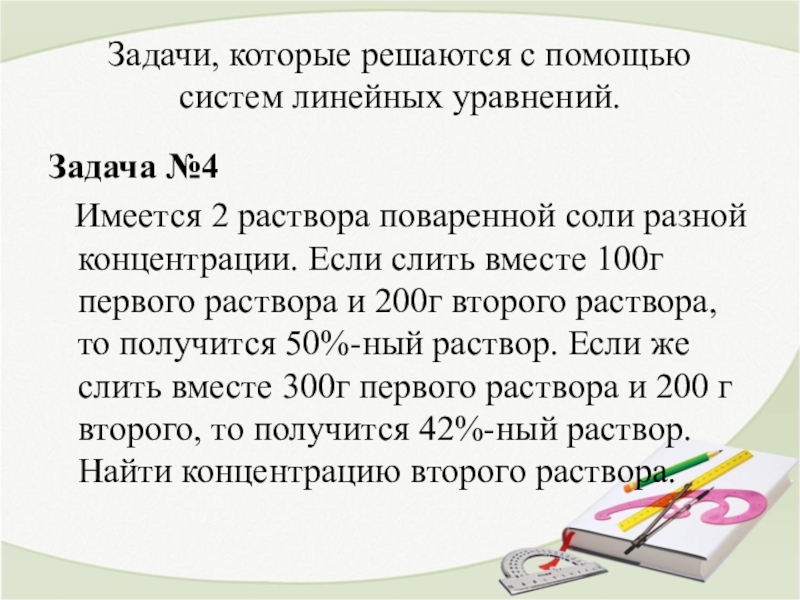
Задача №4
Имеется
2 раствора поваренной соли разной концентрации. Если слить вместе 100г
первого раствора и 200г второго раствора, то получится 50%-ный раствор. Если же слить вместе 300г первого раствора и 200 г второго, то получится 42%-ный раствор. Найти концентрацию второго раствора.
Слайд 14Решение задачи №4
Пусть процентное содержание соли в первом и втором
растворах p% и q% соответственно, тогда по условиям задачи можно
составить два уравнения:100 p/100 + 200 q/100=50*(100+200)/100
300 p/100 + 200 q/100=42*(300+200)/100.
Упростив эти уравнения и решив систему, получим p=30 и q=60.
Следовательно, концентрация второго раствора равна 60%
Ответ. 60%
Слайд 15Старинная схема решения подобных задач
Смешивая 5% и 40% растворы кислот,
необходимо получить 30% раствор. В каком соотношении их необходимо взять?
Параметры
конечного
продукта
30%
Параметры
исходных
продуктов
5%
40%
Доли
исходных продуктов вконечном продукте
1-ый продукт
2-ой продукт
40-30
30-5
10 частей
25 частей
Ответ:
Соотношение первого и второго растворов – 10:25
Слайд 16Задачи на переливание
При решении этих задач выполняются следующие
допущения: «закон сохранения масс» и «закон сохранения объёмов», как для
всей смеси, так и для каждого её компонента. При этом плотности растворов изменяются не значительно и примерно равны плотности воды.
Слайд 17Теперь покажу, как графические иллюстрации к условию задач помогают найти
правильный путь к ответу на вопрос задачи
Слайд 18Задача №5
Сначала приготовили 25%-ый водный раствор поваренной соли.
Затем одну треть воды выпарили. Найти концентрацию получившегося раствора.
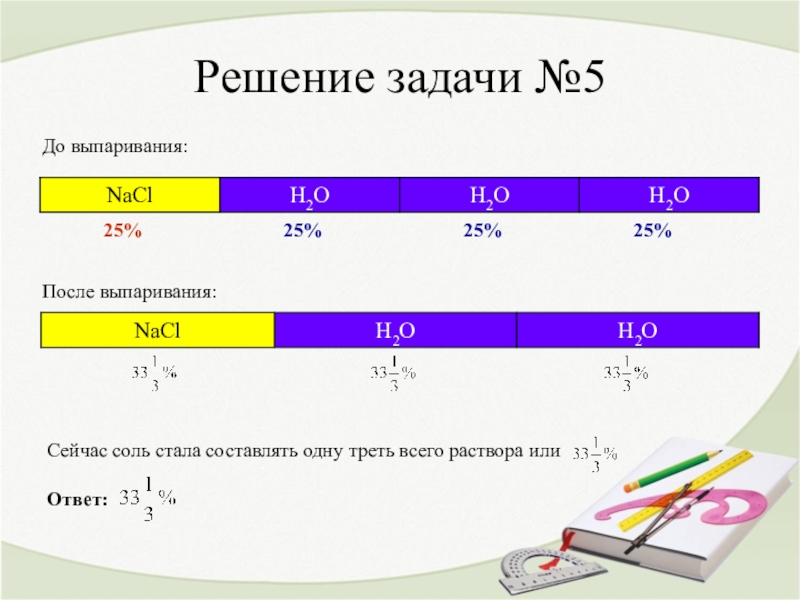
Слайд 19Решение задачи №5
До выпаривания:
После выпаривания:
25%
25%
25% 25%Сейчас соль стала составлять одну треть всего раствора или
Ответ:
Слайд 20Задача №6
Имеется два сплава золота и серебра. В
одном количество этих металлов находится в отношении 1:9, а в
другом 2:3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золота и серебро относилось бы как 1:4?
Слайд 21Решение задачи №6
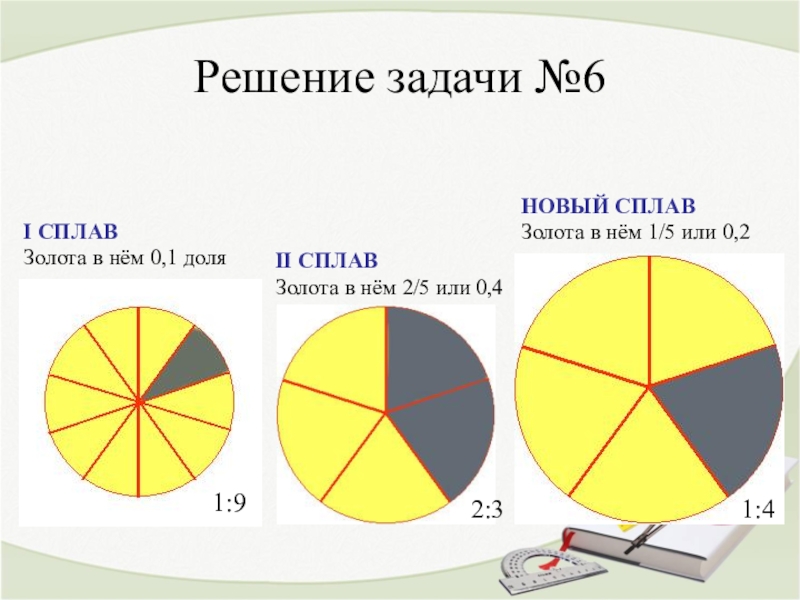
I СПЛАВ
Золота в нём 0,1 доля
II СПЛАВ
Золота в
нём 2/5 или 0,4
НОВЫЙ СПЛАВ
Золота в нём 1/5 или 0,2
1:9
2:3
1:4
Слайд 22Внесём данные в таблицу:
Имеется два сплава золота и серебра. В
одном количество этих металлов находится в отношении 1:9, а в
другом 2:3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золота и серебро относилось бы как 1:4?Решение
0,1х+0,4(15-х) =3
X =10
m (Iсплава) =10 (кг)
m (II сплава) =15–10 =5 (кг)
Ответ: 10 кг, 5 кг.
Слайд 23Вывод
При решении задач следует руководствоваться тем, что при
соединении (разъединении) смесей с одним и тем же чистым веществом
количества чистого вещества и общие количества смесей складываются (вычитаются). Складывать и вычитать доли и процентные содержания нельзя.
Слайд 24Вывод
В ходе проектной деятельности я разделила задачи на растворы и
смеси по типам и нашла единый алгоритм решения для каждого
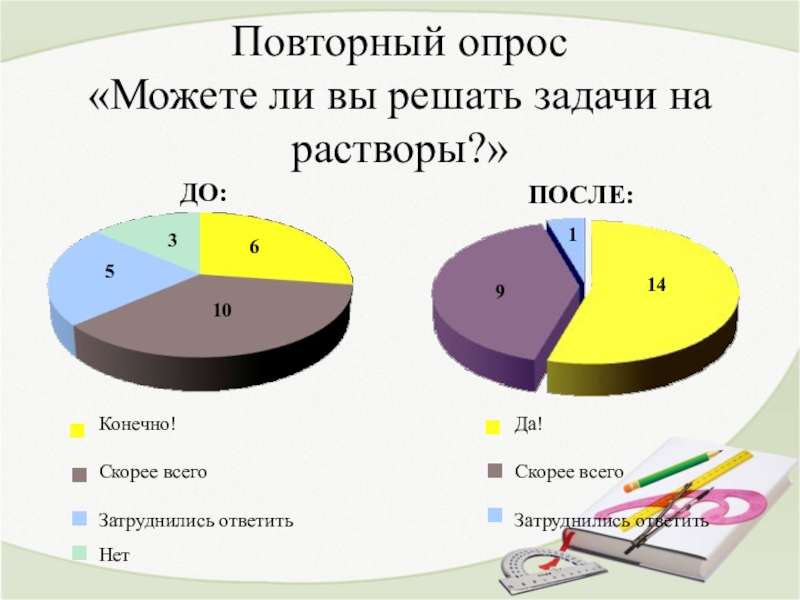
из типов, следовательно, моя гипотеза подтвердилась.
Слайд 25Повторный опрос
«Можете ли вы решать задачи на растворы?»
5
3
6
10
ДО:
Конечно!
Скорее всего
Затруднились ответить
Нет
ПОСЛЕ:
14
9
1
Да!
Скорее
всего
Затруднились ответить
Слайд 26Рефлексия
Как видно из результатов опросов, проектная деятельность помогла мне лучше
понять сущность процентных задач на растворы и смеси и научила
правильно оценивать свои силы.
Слайд 27Список литературы
М.В. Лурье и др. Задачи на составление уравнений, изд-во
«Наука», М., 1976 г.
Н.А. Терёшин Прикладная направленность школьного
курса математики, «Просвещение», М., 1990 г.А.В. Шевкин Школьные математические олимпиады, изд-во «Русское слово», 2002г.
О. Городнова Статья «Учимся решать задачи на «смеси и сплавы», г-та «Математика» №36 за 2004 г.
Слайд 28Интернет-ресурсы
1. Открытый банк заданий ЕГЭ по математике
http://www.mathege.ru
2. Шабон
оформления презентации
http://www.pedsovet.su
