Решение комбинаторных задач с помощью бинома Ньютона и полиномиальной формулы

Содержание

1. Решение комбинаторных задач с помощью бинома Ньютона и полиномиальной формулы
2. Цель:Задачи:изучить и применить бином Ньютона и полиномиальную
3. Язык перечислительной комбинаторики
4. Бином Ньютона и его свойства1.Число всех
5. Треугольник Паскаля……………………………………………………..
6. 11111111111111111702620334455101061515672135352178285656288
7. Некоторые соотношения для биномиальных коэффициентовПолиномиальная формула
8. Задача № 1Доказать, что
9. Доказать неравенство БернуллиЗадача № 2 c >
10. Задача № 3Найти разложение степени бинома Решение.Задача № 4Найти разложение степени тринома
11. Слайд 11
12. Скачать презентанцию

Цель:Задачи:изучить и применить бином Ньютона и полиномиальную формулу к решению некоторых комбинаторных задач 1) ознакомиться с формулой бинома Ньютона и ее свойствами, рассмотреть треугольник Паскаля и метод его построения;2) ознакомиться с

Главная
Математика
Решение комбинаторных задач с помощью бинома Ньютона и полиномиальной формулы

Слайды и текст этой презентации

Слайд 1Научно - практическая конференция школьников "Эврика"
Решение комбинаторных задач с помощью

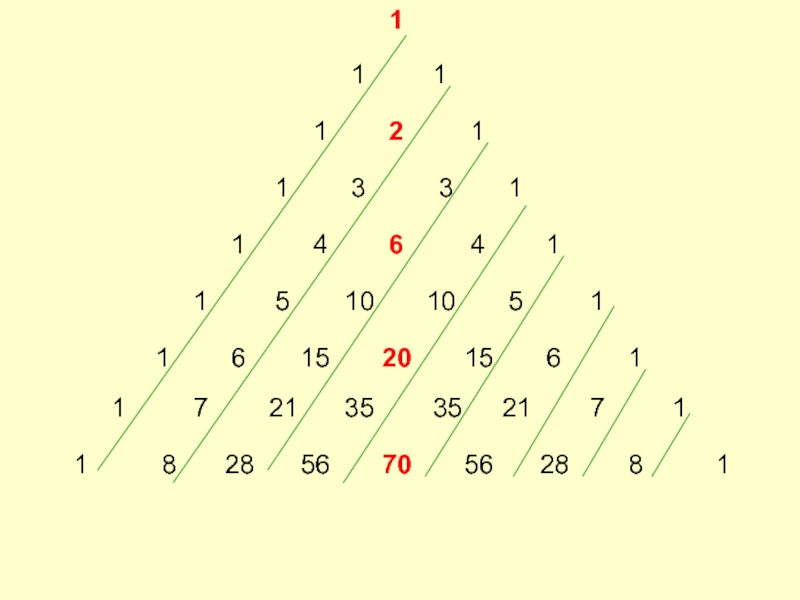
бинома Ньютона и полиномиальной формулы
Научно – исследовательский проект
Выполнен ученицей 10

«А» класса
СОШ № 74 г. Краснодара
Щегольковой Анной

Научный руководитель –
учитель математики СОШ № 74
Забашта Елена Георгиевна

Научно - практическая конференция школьников

Слайд 2Цель:
Задачи:
изучить и применить бином Ньютона и полиномиальную формулу к решению

некоторых комбинаторных задач
1) ознакомиться с формулой бинома Ньютона и

ее свойствами, рассмотреть треугольник Паскаля и метод его построения;

2) ознакомиться с полиномиальной формулой как обобщением бинома Ньютона;

3) рассмотреть некоторые комбинаторные задачи, решаемые с помощью бинома Ньютона и полиномиальной формулы.

Цель:Задачи:изучить и применить бином Ньютона и полиномиальную формулу к решению некоторых комбинаторных задач 1) ознакомиться с формулой

Слайд 3Язык перечислительной комбинаторики

Слайд 4Бином Ньютона и его свойства

1.Число всех членов разложения на единицу

больше показателя степени бинома, т.е. равно n + 1.
2. Сумма

показателей степени a и b каждого члена разложения равна показателю степени бинома.
3. Общий член разложения имеет вид

4. Коэффициенты разложения, одинаково удаленные от концов разложения,
равны между собой . Правило симметрии

5. Правило Паскаля

Бином Ньютона и его свойства1.Число всех членов разложения на единицу больше показателя степени бинома, т.е. равно

Слайд 5Треугольник Паскаля

……………………………………………………..

Слайд 61
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
70
2
6
20
3
3
4
4
5
5
10
10
6
15
15
6
7
21
35
35
21
7
8
28
56
56
28
8

Слайд 7

Некоторые соотношения для биномиальных коэффициентов
Полиномиальная формула

Слайд 8

Задача № 1

Доказать, что

делится нацело на 64 при любом натуральном n.

Доказательство.

Обозначив выражение в скобках через а, а N, имеем:

Полученная сумма делится на 64, что и требовалось доказать.

Слайд 9Доказать неравенство Бернулли
Задача № 2
c > 1 + n

(c – 1), где с – произвольное число, большее 1,

n – натуральное число, большее 1.

Доказательство.

Для каждого натурального n и чисел a = 1 и b = c-1 верны равенства

По условию b > 0 и n > 2. Следовательно, каждое слагаемое (их по меньшей мере три) в полученной сумме строго положительно. Значит,

> 1 + nb

и доказываемое неравенство верно.

Доказать неравенство БернуллиЗадача № 2 c > 1 + n (c – 1), где с – произвольное

Слайд 10Задача № 3
Найти разложение степени бинома

Решение.

Задача № 4
Найти разложение

степени тринома

Слайд 11

Скачать презентацию

Теги

Разделы презентаций

Решение комбинаторных задач с помощью бинома Ньютона и полиномиальной формулы

Содержание

Слайды и текст этой презентации

Слайд 1Научно - практическая конференция школьников "Эврика"
Решение комбинаторных задач с помощью

бинома Ньютона и полиномиальной формулы
Научно – исследовательский проект
Выполнен ученицей 10

Слайд 2Цель:
Задачи:
изучить и применить бином Ньютона и полиномиальную формулу к решению

некоторых комбинаторных задач
1) ознакомиться с формулой бинома Ньютона и

Слайд 3Язык перечислительной комбинаторики

Слайд 4Бином Ньютона и его свойства

1.Число всех членов разложения на единицу

больше показателя степени бинома, т.е. равно n + 1.
2. Сумма

Слайд 5Треугольник Паскаля

……………………………………………………..

Слайд 61
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
70
2
6
20
3
3
4
4
5
5
10
10
6
15
15
6
7
21
35
35
21
7
8
28
56
56
28
8

Слайд 7

Некоторые соотношения для биномиальных коэффициентов
Полиномиальная формула

Слайд 8

Задача № 1

Доказать, что

Слайд 9Доказать неравенство Бернулли
Задача № 2
c > 1 + n

(c – 1), где с – произвольное число, большее 1,

Слайд 10Задача № 3
Найти разложение степени бинома

Решение.

Задача № 4
Найти разложение

степени тринома

Слайд 11

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Решение комбинаторных задач с помощью бинома Ньютона и полиномиальной формулы

Содержание

Слайды и текст этой презентации

Слайд 1Научно - практическая конференция школьников "Эврика"Решение комбинаторных задач с помощью

бинома Ньютона и полиномиальной формулыНаучно – исследовательский проектВыполнен ученицей 10

Слайд 2Цель:Задачи:изучить и применить бином Ньютона и полиномиальную формулу к решению

некоторых комбинаторных задач 1) ознакомиться с формулой бинома Ньютона и

Слайд 3Язык перечислительной комбинаторики

Слайд 4Бином Ньютона и его свойства1.Число всех членов разложения на единицу

больше показателя степени бинома, т.е. равно n + 1.2. Сумма

Слайд 5Треугольник Паскаля……………………………………………………..

Слайд 611111111111111111702620334455101061515672135352178285656288

Слайд 7Некоторые соотношения для биномиальных коэффициентовПолиномиальная формула

Слайд 8Задача № 1Доказать, что

Слайд 9Доказать неравенство БернуллиЗадача № 2 c > 1 + n

(c – 1), где с – произвольное число, большее 1,

Слайд 10Задача № 3Найти разложение степени бинома Решение.Задача № 4Найти разложение

степени тринома

Слайд 11

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Научно - практическая конференция школьников "Эврика"
Решение комбинаторных задач с помощью

бинома Ньютона и полиномиальной формулы
Научно – исследовательский проект
Выполнен ученицей 10

Слайд 2Цель:
Задачи:
изучить и применить бином Ньютона и полиномиальную формулу к решению

некоторых комбинаторных задач
1) ознакомиться с формулой бинома Ньютона и

Слайд 4Бином Ньютона и его свойства

1.Число всех членов разложения на единицу

больше показателя степени бинома, т.е. равно n + 1.
2. Сумма

Слайд 5Треугольник Паскаля

……………………………………………………..

Слайд 61
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
70
2
6
20
3
3
4
4
5
5
10
10
6
15
15
6
7
21
35
35
21
7
8
28
56
56
28
8

Слайд 7

Некоторые соотношения для биномиальных коэффициентов
Полиномиальная формула

Слайд 8

Задача № 1

Доказать, что

Слайд 9Доказать неравенство Бернулли
Задача № 2
c > 1 + n

Слайд 10Задача № 3
Найти разложение степени бинома

Решение.

Задача № 4
Найти разложение