Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к открытому уроку "Логарифмическая функция"
Содержание
- 1. Презентация к открытому уроку "Логарифмическая функция"
- 2. Девиз урока: Древняя китайская мудростьСкажи мне –
- 3. 2=3? 4 – 10
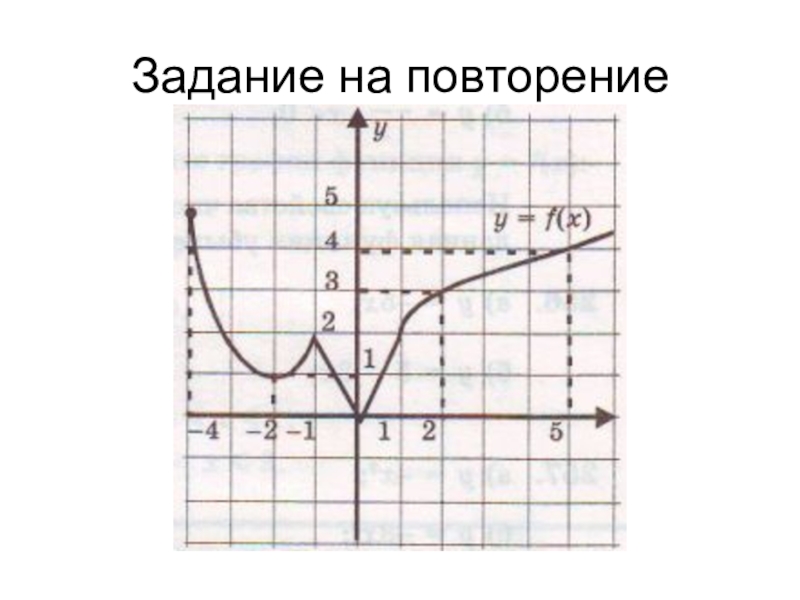
- 4. Задание на повторение
- 5. Если я знаю, что я знаю мало,я добьюсь того чтобы знать БОЛЬШЕ
- 6. Тема урокаЛогарифмическая функция ее свойства и график
- 7. Определение: Логарифмической функцией называется функция
- 8. Цель работыПостроение графика логарифмической функцииЕе исследованиеОсновные свойства
- 9. Нет лучших знаний, чем знания, добытые собственным трудом
- 10.
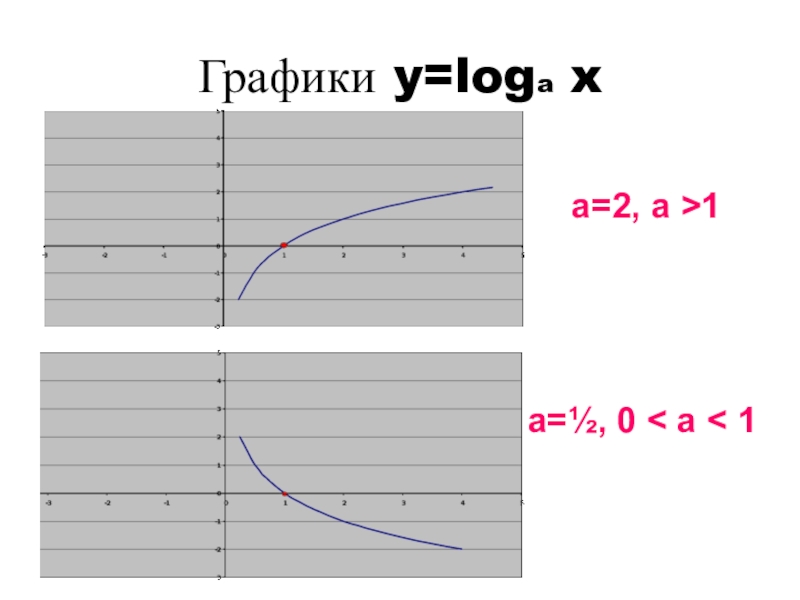
- 11. Графики y=loga x а=2, a >1а=½, 0 < a < 1
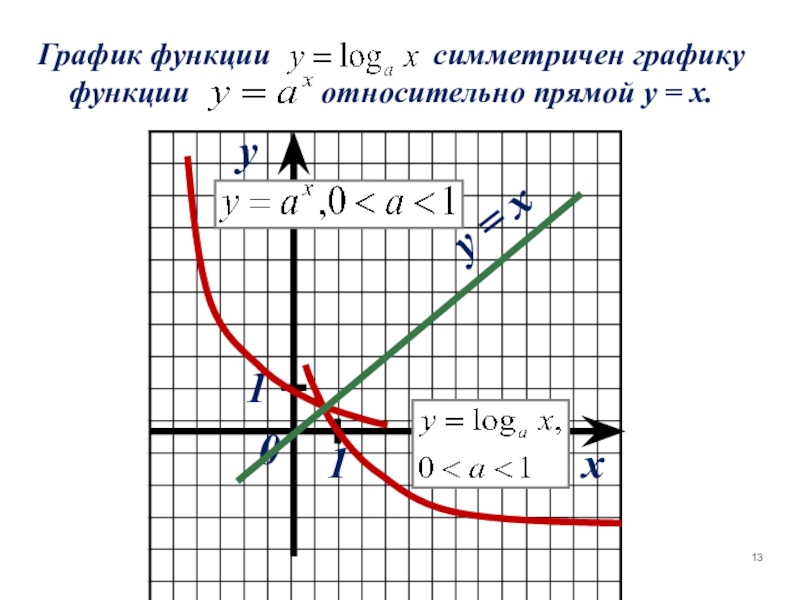
- 12. xy0aay = x11 График функции
- 13. xyy = x110 График функции
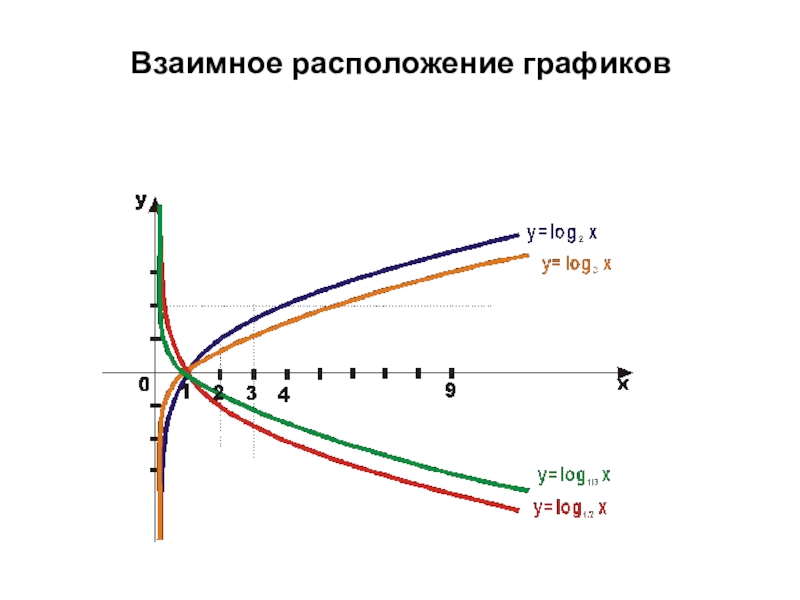
- 14. Взаимное расположение графиков
- 15. Свойства логарифмической функции y = loga x
- 16. Выяснить, является положительным или отрицательным число:1) log3
- 17. Сравните числа:1) log3 и log32) log
- 18. Логарифмическая «комедия 2>3»Комедия начинается с неравенства,
- 19. Преобразование графиков логарифмической функцииУмение, даже схематично, строить
- 20. -?-?
- 21. -?-?
- 22. 2log2+=xy-?-?
- 23. 2log2–=xy-?-?
- 24. -?-?
- 25. Логарифмы в окружающем мире.
- 26. Испокон веков целью математической науки было помочь
- 27. Уравнение логарифмической спирали в полярной системе координат
- 28. Известно, что живые существа обычно растут, сохраняя
- 29. А такой рост может совершаться лишь по
- 30. Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям
- 31. По логарифмическим спиралям закручены и многие галактики,в частности Галактика, которой принадлежит Солнечная система.
- 32. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.
- 33. Логарифмическую спираль можно встретить и в архитектуре.Шуховская башня в Москве.
- 34. Иоганн-Вольфганг Гёте считал : Логарифмическая спираль есть математический символ жизни и духовного развития.
- 35. Домашнее задание§16 стр.121 График, свойства(выучить)№ 256, 257,261,263(2,3)
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Девиз урока:
Древняя китайская мудрость
Скажи мне – и я забуду,
покажи
мне – и я запомню,
пойму.Слайд 32=3?
4 – 10 = 9 –
15 Верно?
Где ошибка??
Ошибка заключается при извлечении
Прибавим к обеим частям
,получим 4-10 + = 9-15+
Верно??
Выделим квадрат двучлена
Верно ??
Из обеих частей извлечём
: Верно??
Взаимно уничтожается,
имеем 2=3
Верно??
Слайд 7
Определение:
Логарифмической функцией называется функция вида
y =
logax,
где а - заданное число,
а > 0, а ≠
1. Слайд 11Графики y=loga x
а=2, a >1
а=½, 0 < a
Слайд 15
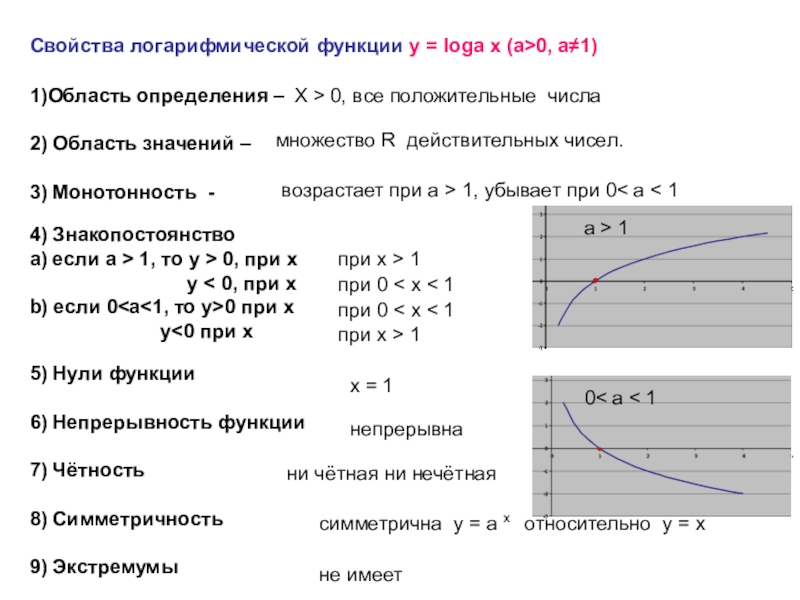
Свойства логарифмической функции y = loga x (а>0, а≠1)
1)Область
определения –
2) Область значений –
3) Монотонность -
4) Знакопостоянство
а) если
a > 1, то y > 0, при хy < 0, при х
b) если 0
y<0 при x
5) Нули функции
6) Непрерывность функции
7) Чётность
8) Симметричность
9) Экстремумы
X > 0, все положительные числа
множество R действительных чисел.
возрастает при a > 1, убывает при 0< a < 1
при х > 1
при 0 < х < 1
при 0 < х < 1
при х > 1
х = 1
непрерывна
ни чётная ни нечётная
симметрична у = а х относительно у = х
не имеет
0< a < 1
a > 1
Слайд 16Выяснить, является положительным или отрицательным число:
1) log3 4.5;
2) log3 0,45;
3)
log0,5 0,25;
4) log0,5 9,6.
> 0
< 0
> 0
< 0
Слайд 18Логарифмическая «комедия 2>3»
Комедия начинается с неравенства,
бесспорно правильно.
Затем
следует преобразование
Тоже не внушающее сомнения
Большему числу соответствует больший логарифм, если
функция возрастает, значит,После сокращения на
Имеем 2>3.
В чем ошибка этого доказательства?
Слайд 19Преобразование графиков логарифмической функции
Умение, даже схематично, строить графики функций, по
их свойствам,и проводить преобразования графиков поможет вам при сдаче ЕНТ
Например
при нахождении обл.определения и обл.значенийСлайд 26 Испокон веков целью математической науки было помочь людям узнать больше
об окружающем мире, познать его закономерности и тайны. Ряд явлений
природы помогает описать именно логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции. Одним из наиболее наглядных примеров такого обращения является логарифмическая спираль.Слайд 27 Уравнение логарифмической спирали в полярной системе координат имеет вид
, где
Переписав уравнение в виде
мы увидим, что величина полярного угла пропорциональна логарифму радиус-вектора. Отсюда и происходит название логарифмическая спираль.
Логарифмическая спираль
Слайд 28 Известно, что живые существа обычно растут, сохраняя общее начертание своей
формы. При этом чаще всего они растут во всех направлениях
– взрослое существо и выше и толще детёныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем рост совершается так, что сохраняется подобие раковины сеё первоначальной формой.









 1а=½, 0 < a < 1" alt="Графики y=loga x а=2, a >1а=½, 0 < a < 1">
1а=½, 0 < a < 1" alt="Графики y=loga x а=2, a >1а=½, 0 < a < 1">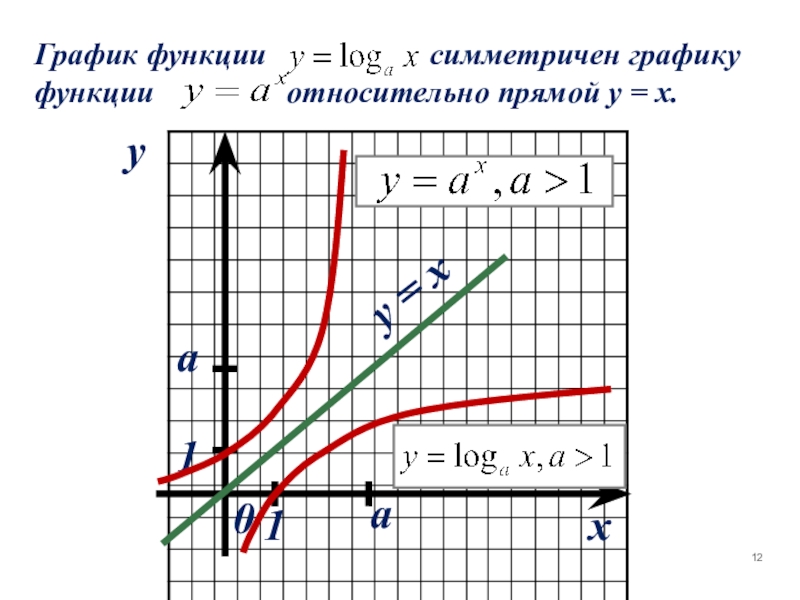
 0, а≠1) 1)Область определения" alt="Свойства логарифмической функции y = loga x (а>0, а≠1) 1)Область определения –2) Область значений –3) Монотонность -">
0, а≠1) 1)Область определения" alt="Свойства логарифмической функции y = loga x (а>0, а≠1) 1)Область определения –2) Область значений –3) Монотонность -">

 3»Комедия начинается с неравенства, бесспорно правильно.Затем следует преобразованиеТоже" alt="Логарифмическая «комедия 2>3»Комедия начинается с неравенства, бесспорно правильно.Затем следует преобразованиеТоже не внушающее сомненияБольшему числу соответствует больший">
3»Комедия начинается с неравенства, бесспорно правильно.Затем следует преобразованиеТоже" alt="Логарифмическая «комедия 2>3»Комедия начинается с неравенства, бесспорно правильно.Затем следует преобразованиеТоже не внушающее сомненияБольшему числу соответствует больший">