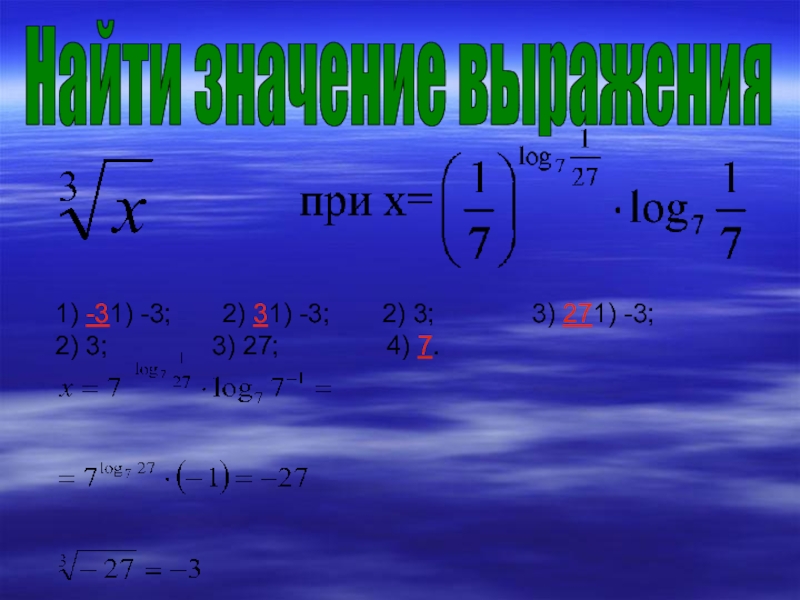Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение логарифмических неравенств
Содержание
- 1. Решение логарифмических неравенств
- 2. Свойства логарифмов
- 3. 1) 21) 2;
- 4. Вы ответили неверно!
- 5. Вы ответили верноОбъясните решение
- 6. Найти значение выражения1) 21) 2;
- 7. Найти значение выражения1) 3;
- 8. Вы ответили неверно!
- 9. Вы ответили верноОбъясните решение
- 10. Найти значение выражения1) 3;
- 11. Найти значение выражения1) -31) -3; 2) 31)
- 12. Вы ответили неверно!
- 13. Вы ответили верноОбъясните решение
- 14. Найти значение выражения1) -31) -3; 2) 31)
- 15. Исследовательская работаИстория изобретения логарифмовАвтор ученица 11 класса Бондарева Л.
- 16. Слайд 16
- 17. Астрономы просто могли утонуть в невыполнимых расчётах.
- 18. Логарифмы изобрели независимо друг от друга Джон
- 19. Первый изобретатель логарифмов – шотландский барон Джон
- 20. В 1620 году швейцарец Иост
- 21. Однако таблицы Бюрги не получили
- 22. Открытие Непера в первые же годы приобрело
- 23. Слайд 23
- 24. Схемы равносильных преобразований при решении неравенств
- 25. t+-+Введём замену:-2Вернемся к замене:х09Ответ: х (0; ) (9; )
- 26. Слайд 26
- 27. Средний уровеньРешите неравенствоДостаточный уровеньУкажите сумму целых решений неравенстваВысокий уровеньРешите самостоятельно
- 28. Слайд 28
- 29. Домашнее задание§ 18 (пример №4),№ 18.17(г),№ 18.18(г),№ 18.20(б).
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 31) 21) 2;
2) -21) 2;
2) -2; 3) 11) 2; 2) -2; 3) 1; 4) 4;Найти значение выражения
1) 21) 2; 2) -21) 2; 2) -2; 3) 11) 2; 2) -2; 3) 1; 4) 4;
Слайд 7Найти значение выражения
1) 3;
2) 625;
3) 81; 4) 1.1) 31) 3; 2) 6251) 3; 2) 625; 3) 811) 3; 2) 625; 3) 81; 4) 1.
Слайд 10Найти значение выражения
1) 3;
2) 625;
3) 81; 4) 1.1) 31) 3; 2) 6251) 3; 2) 625; 3) 811) 3; 2) 625; 3) 81; 4) 1.
Слайд 16
На всём протяжении
XVI века быстро возрастало количество приближённых вычислений, прежде всего в астрономии.Исследование планетных движений требовало колоссальных расчётов.
На всём протяжении
XVI века быстро возрастало количество приближённых вычислений, прежде всего в астрономии.
Исследование планетных движений требовало колоссальных расчётов.
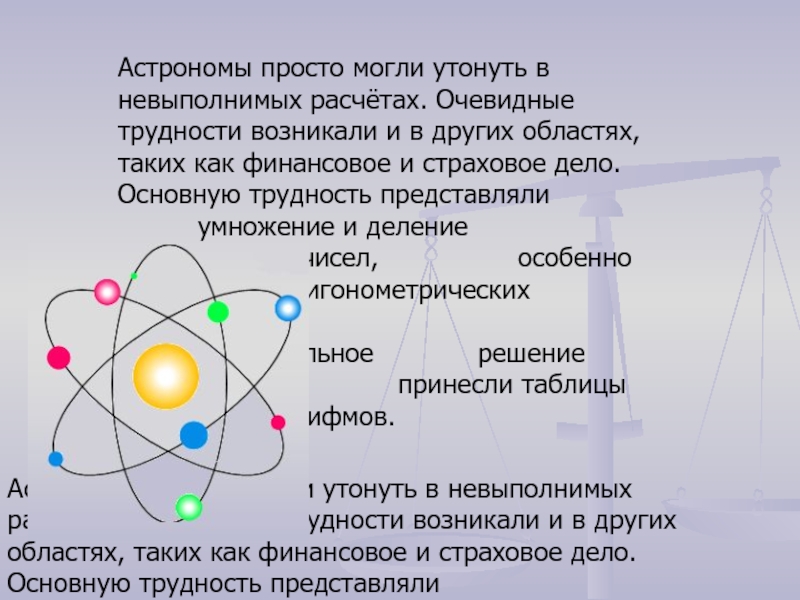
Слайд 17Астрономы просто могли утонуть в невыполнимых расчётах. Очевидные трудности возникали
и в других областях, таких как финансовое и страховое дело.
Основную трудность представляли умножение и деление многозначных чисел, особенно тригонометрических величин. Удовлетворительное решение этого вопроса принесли таблицы логарифмов.Астрономы просто могли утонуть в невыполнимых расчётах. Очевидные трудности возникали и в других областях, таких как финансовое и страховое дело. Основную трудность представляли умножение и деление многозначных чисел, особенно тригонометрических величин. Удовлетворительное решение этого вопроса принесли таблицы логарифмов.
Слайд 18
Логарифмы изобрели независимо друг от друга Джон Непер и Иост
Бюрге. Их цель была одна - желание дать новое удобное
средство арифметических вычислений. Подход же оказался разный. Непер кинематически выразил логарифмическую ф - ию, что позволило ему по существу вступить в почти неизведанную область теории ф – ий. Бюрги остался на почве рассмотрения дискретных прогрессий. У обоих определение логарифма не походило на современное.Слайд 19 Первый изобретатель логарифмов – шотландский барон Джон Непер (1550-1617) получил
образование на родине в Эдинбурге. Затем после путешествия по Германии,
Франции и Испании, в возрасте 21 года, он навсегда поселился в семейном поместье близ Эдинбурга. Непер занялся главным образом богословием и математикой, которую изучал по сочинениям Евклида, Архимеда, Региомонтана, Коперника. К открытию логарифмов Непер пришел не позднее 1594 года, но лишь 20 лет спустя опубликовал своё «Описание удивительной таблицы логарифмов» (1614). Первый изобретатель логарифмов – шотландский барон Джон Непер (1550-1617) получил образование на родине в Эдинбурге. Затем после путешествия по Германии, Франции и Испании, в возрасте 21 года, он навсегда поселился в семейном поместье близ Эдинбурга. Непер занялся главным образом богословием и математикой, которую изучал по сочинениям Евклида, Архимеда, Региомонтана, Коперника. К открытию логарифмов Непер пришел не позднее 1594 года, но лишь 20 лет спустя опубликовал своё «Описание удивительной таблицы логарифмов» (1614).