Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрический смысл производной. Решение задач из ЕГЭ
Содержание
- 1. Геометрический смысл производной. Решение задач из ЕГЭ
- 2. На рисунке изображены график функции y=f(x) и
- 3. На рисунке изображены график функции y=f(x) и
- 4. На рисунке изображены график функции y=f(x) и
- 5. На рисунке изображен график функции y=f `(x)
- 6. На рисунке изображен график функции y=f (x),
- 7. На рисунке изображен график y=f `(x) –
- 8. На рисунке изображен график y=f `(x) –
- 9. На рисунке изображен график y=f `(x) –
- 10. На рисунке изображен график y=f `(x) –
- 11. На рисунке изображен график y=f `(x) –
- 12. На рисунке изображен график y=f `(x) –
- 13. На рисунке изображен график y=f `(x) –
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Геометрический смысл производной. Решение задач из ЕГЭ.
Автор презентации: Белякова Ольга
Владимировна,
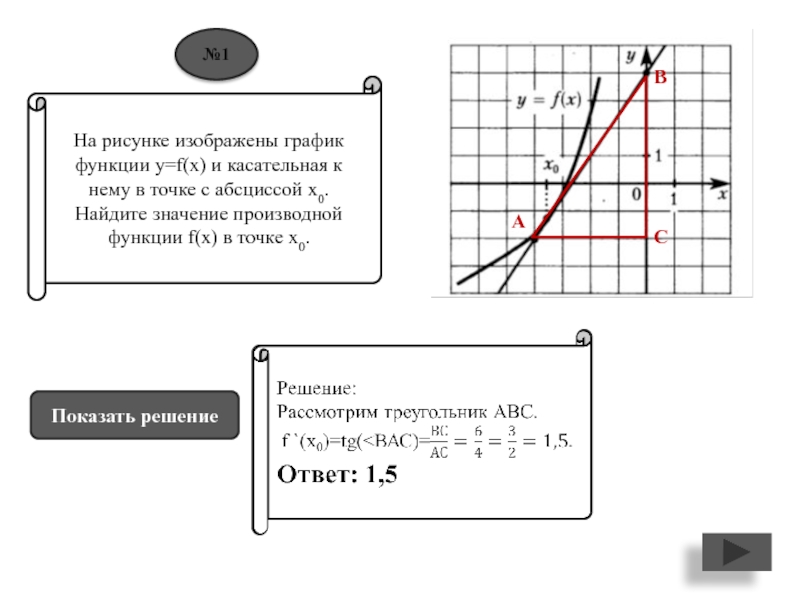
Слайд 2На рисунке изображены график функции y=f(x) и касательная к нему
в точке с абсциссой х0. Найдите значение производной функции f(x)
в точке х0.Показать решение
№1
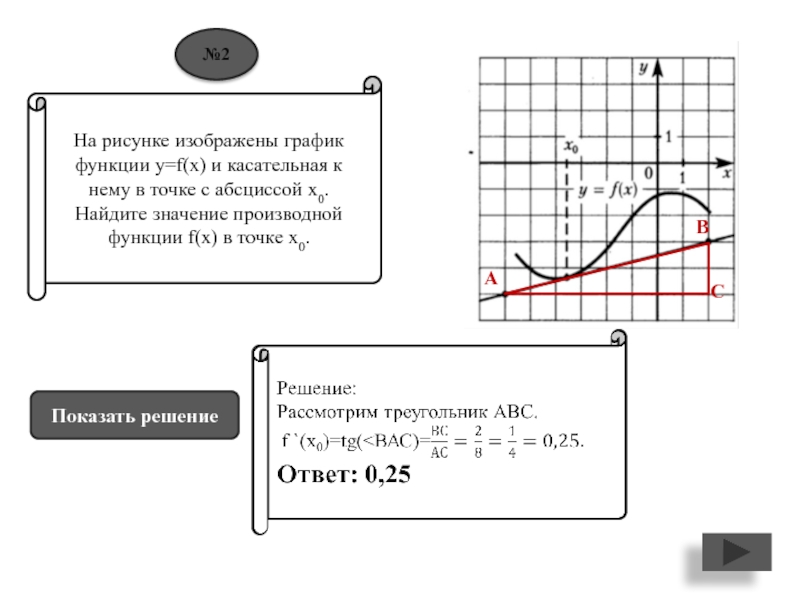
Слайд 3На рисунке изображены график функции y=f(x) и касательная к нему
в точке с абсциссой х0. Найдите значение производной функции f(x)
в точке х0.Показать решение
№2
Слайд 4На рисунке изображены график функции y=f(x) и касательная к нему
в точке с абсциссой х0. Найдите значение производной функции f(x)
в точке х0.Показать решение
№3
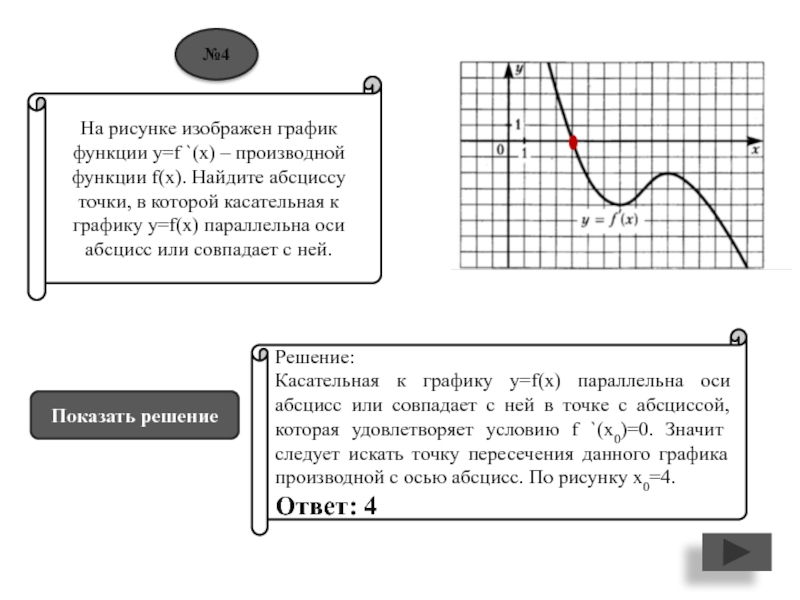
Слайд 5На рисунке изображен график функции y=f `(x) – производной функции
f(x). Найдите абсциссу точки, в которой касательная к графику y=f(x)
параллельна оси абсцисс или совпадает с ней.Решение:
Касательная к графику y=f(x) параллельна оси абсцисс или совпадает с ней в точке с абсциссой, которая удовлетворяет условию f `(x0)=0. Значит следует искать точку пересечения данного графика производной с осью абсцисс. По рисунку х0=4.
Ответ: 4
Показать решение
№4
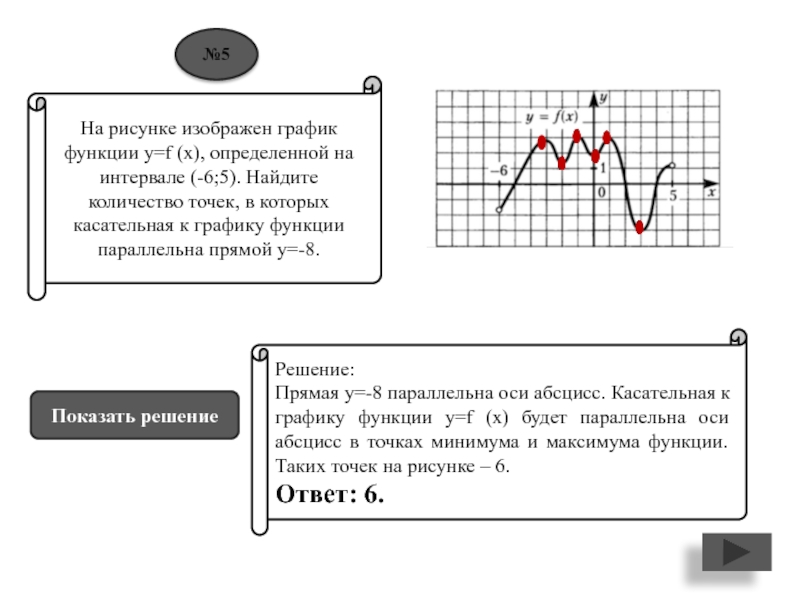
Слайд 6На рисунке изображен график функции y=f (x), определенной на интервале
(-6;5). Найдите количество точек, в которых касательная к графику функции
параллельна прямой у=-8.Решение:
Прямая у=-8 параллельна оси абсцисс. Касательная к графику функции y=f (x) будет параллельна оси абсцисс в точках минимума и максимума функции. Таких точек на рисунке – 6.
Ответ: 6.
Показать решение
№5
Слайд 7На рисунке изображен график y=f `(x) – производной функции f(x),
определенной на интервале (-1;12). Найдите количество точек, в которых касательная
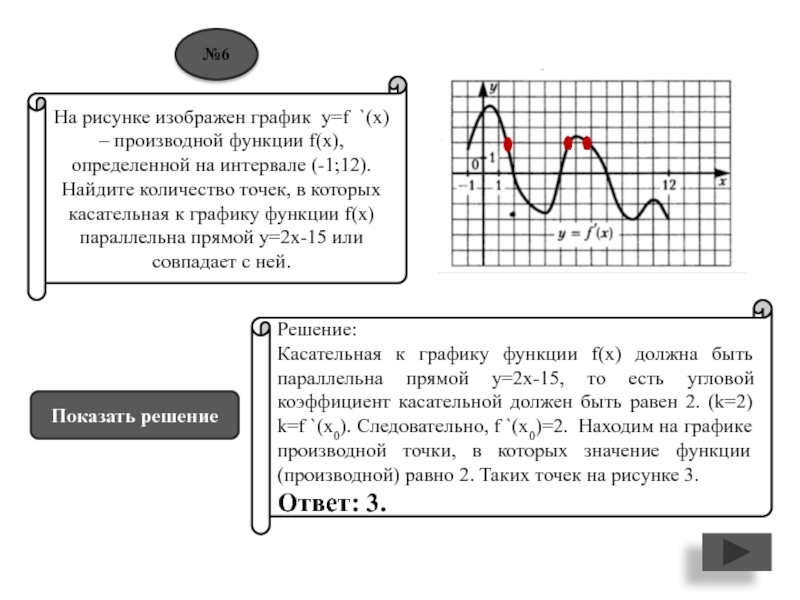
к графику функции f(x) параллельна прямой у=2х-15 или совпадает с ней.Решение:
Касательная к графику функции f(x) должна быть параллельна прямой у=2х-15, то есть угловой коэффициент касательной должен быть равен 2. (k=2) k=f `(x0). Следовательно, f `(x0)=2. Находим на графике производной точки, в которых значение функции (производной) равно 2. Таких точек на рисунке 3.
Ответ: 3.
Показать решение
№6
Слайд 8На рисунке изображен график y=f `(x) – производной функции f(x),
определенной на интервале (-9;8). Найдите количество точек, в которых касательная
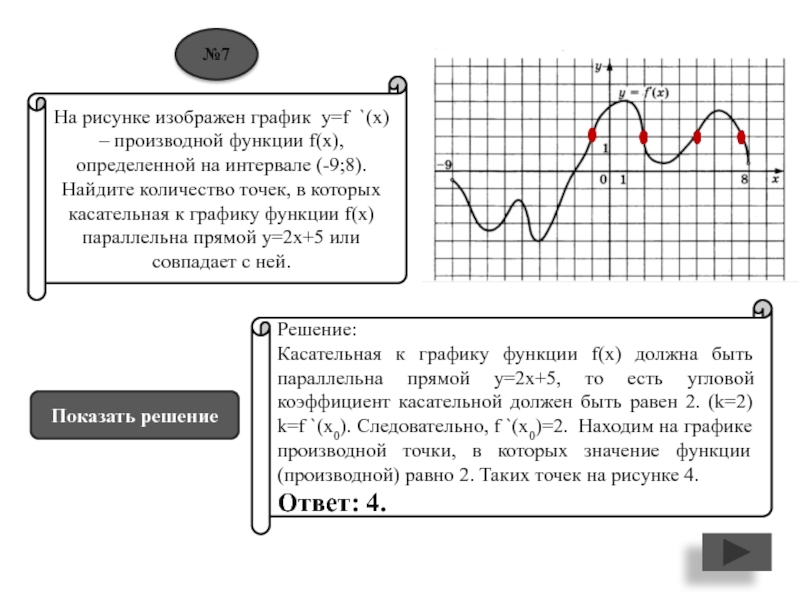
к графику функции f(x) параллельна прямой у=2х+5 или совпадает с ней.Решение:
Касательная к графику функции f(x) должна быть параллельна прямой у=2х+5, то есть угловой коэффициент касательной должен быть равен 2. (k=2) k=f `(x0). Следовательно, f `(x0)=2. Находим на графике производной точки, в которых значение функции (производной) равно 2. Таких точек на рисунке 4.
Ответ: 4.
Показать решение
№7
Слайд 9На рисунке изображен график y=f `(x) – производной функции f(x),
определенной на интервале (-8;5). В какой точке отрезка [-3;2] f(x)
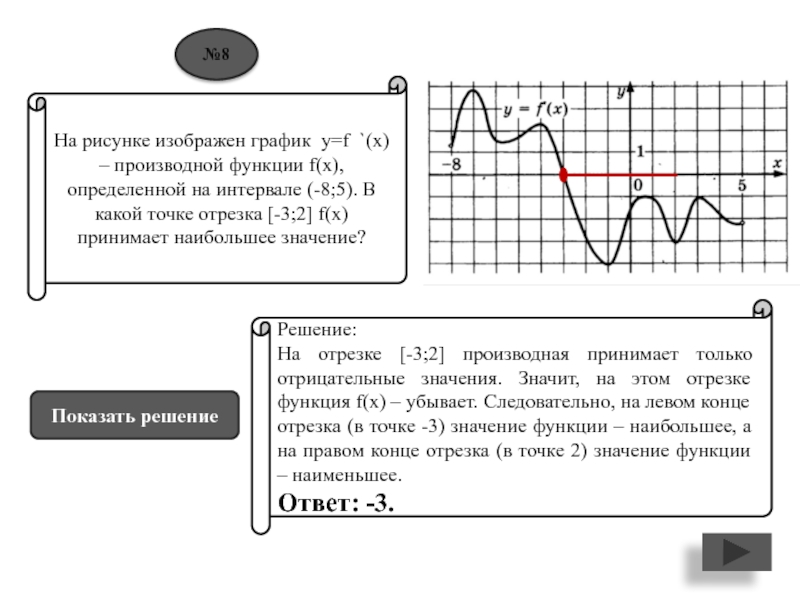
принимает наибольшее значение?Решение:
На отрезке [-3;2] производная принимает только отрицательные значения. Значит, на этом отрезке функция f(x) – убывает. Следовательно, на левом конце отрезка (в точке -3) значение функции – наибольшее, а на правом конце отрезка (в точке 2) значение функции – наименьшее.
Ответ: -3.
Показать решение
№8
Слайд 10На рисунке изображен график y=f `(x) – производной функции f(x),
определенной на интервале (-2;9). В какой точке отрезка [1;5] f(x)
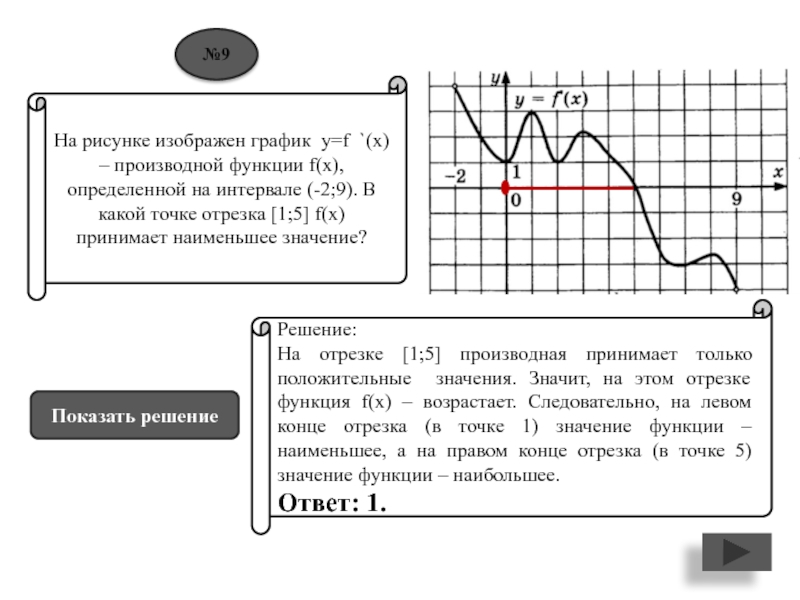
принимает наименьшее значение?Решение:
На отрезке [1;5] производная принимает только положительные значения. Значит, на этом отрезке функция f(x) – возрастает. Следовательно, на левом конце отрезка (в точке 1) значение функции – наименьшее, а на правом конце отрезка (в точке 5) значение функции – наибольшее.
Ответ: 1.
Показать решение
№9
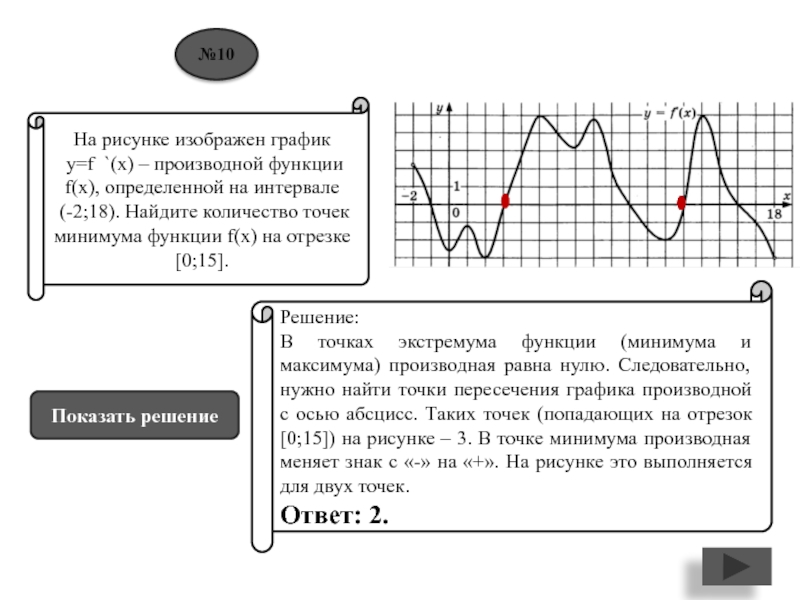
Слайд 11На рисунке изображен график
y=f `(x) – производной функции
f(x), определенной на интервале
(-2;18). Найдите количество точек минимума функции
f(x) на отрезке [0;15].Решение:
В точках экстремума функции (минимума и максимума) производная равна нулю. Следовательно, нужно найти точки пересечения графика производной с осью абсцисс. Таких точек (попадающих на отрезок [0;15]) на рисунке – 3. В точке минимума производная меняет знак с «-» на «+». На рисунке это выполняется для двух точек.
Ответ: 2.
Показать решение
№10
Слайд 12На рисунке изображен график
y=f `(x) – производной функции
f(x), определенной на интервале
(-3;11). Найдите промежутки убывания функции f(x).
В ответе укажите длину наибольшего из них.Решение:
На промежутке убывания функции f(x), ее производная отрицательна. На рисунке есть два промежутка, на которых производная функции принимает отрицательные значения. Это отрезки [-2;2] и [6;10] . Длина первого отрезка=2-(-2)=4. Длина второго отрезка=10-6=4. Длины обоих отрезков одинаковы.
Ответ: 4.
Показать решение
№11
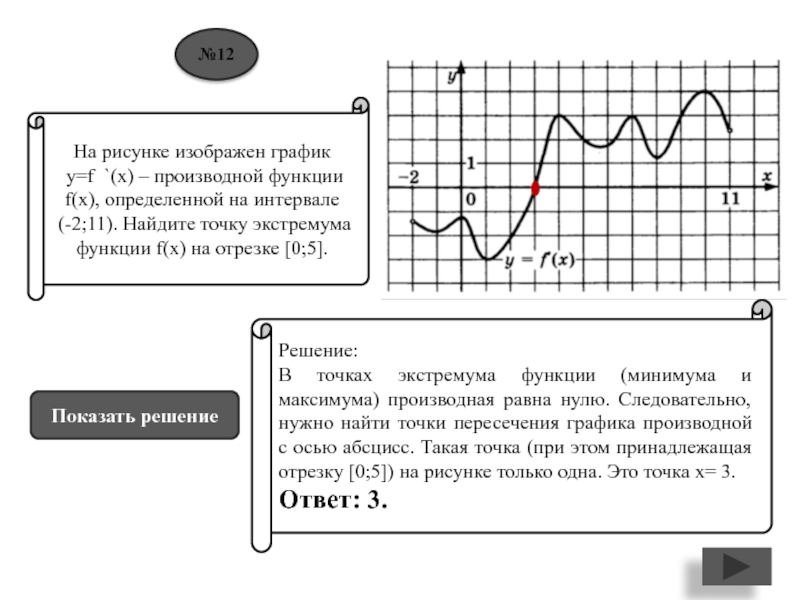
Слайд 13На рисунке изображен график
y=f `(x) – производной функции
f(x), определенной на интервале
(-2;11). Найдите точку экстремума функции f(x)
на отрезке [0;5].Решение:
В точках экстремума функции (минимума и максимума) производная равна нулю. Следовательно, нужно найти точки пересечения графика производной с осью абсцисс. Такая точка (при этом принадлежащая отрезку [0;5]) на рисунке только одна. Это точка х= 3.
Ответ: 3.
Показать решение
№12