Решение простейших тригонометрических уравнений

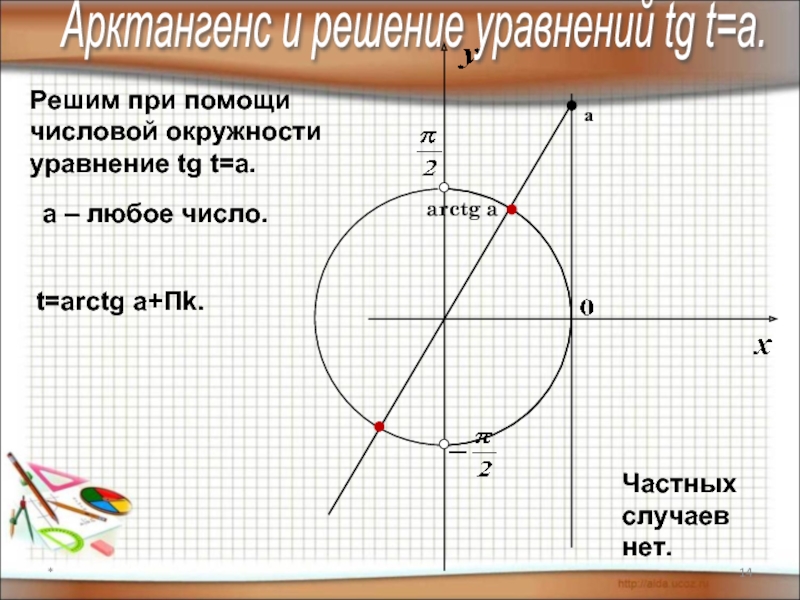
определять значения синуса, косинуса,
тангенса и котангенса для точек числовой

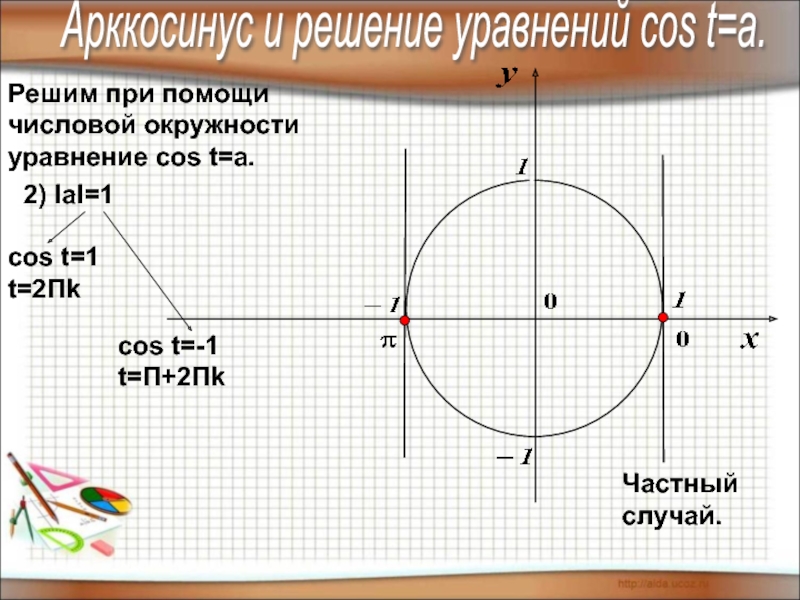
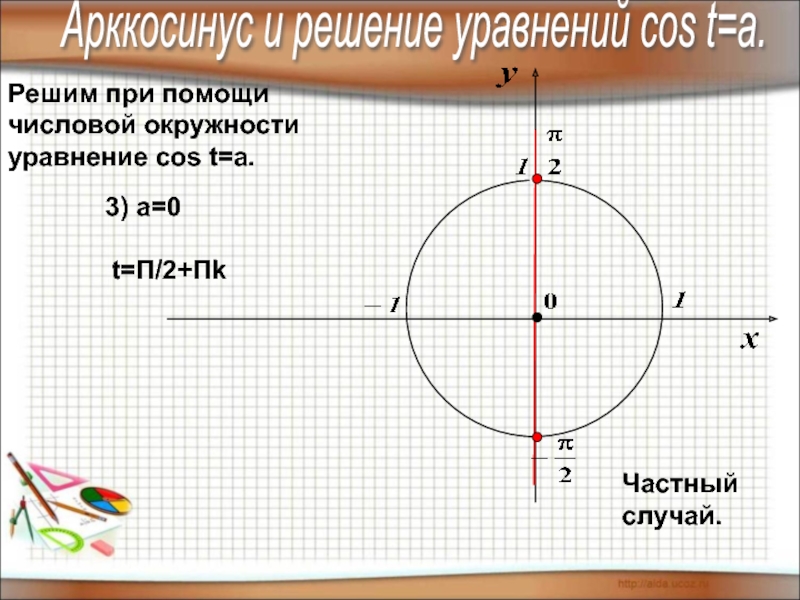
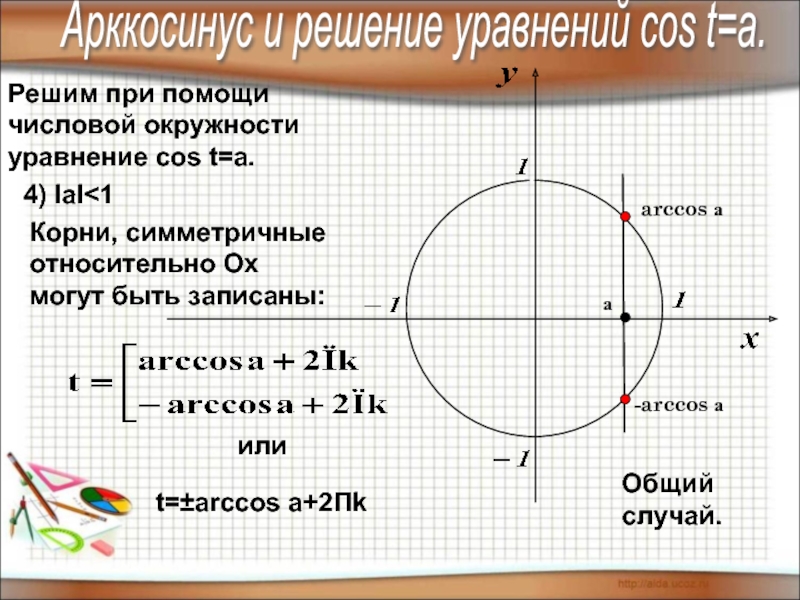
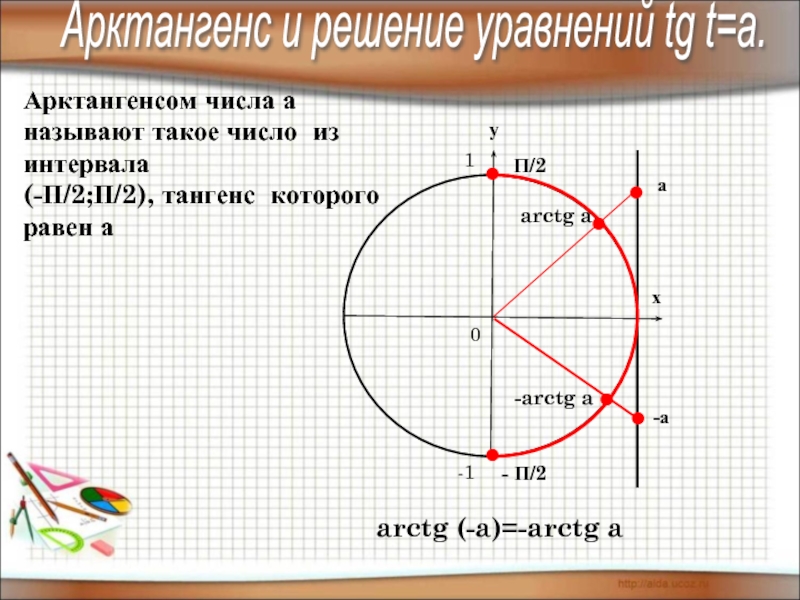
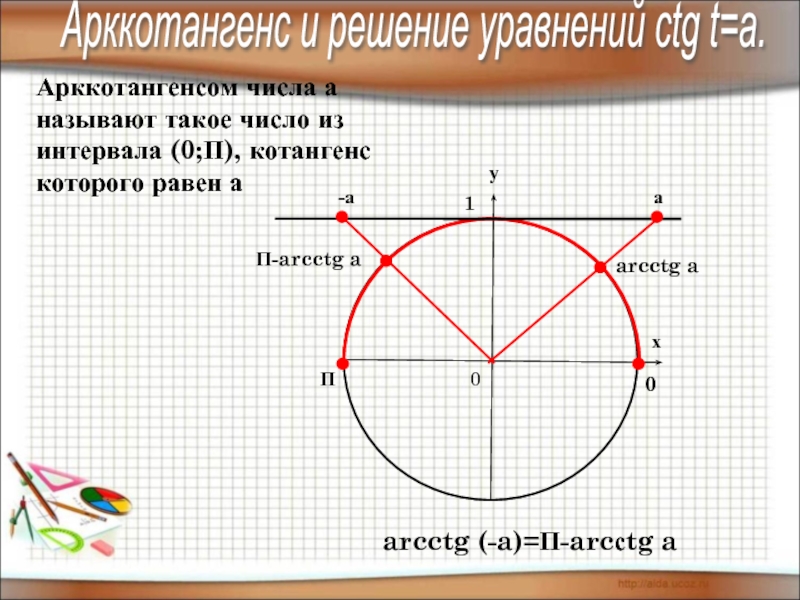
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.

1) уметь отмечать точки на числовой
окружности;

3) знать свойства основных
тригонометрических функций;

П/2; П/2], синус которого равен а.


arcsin а
П/2
- П/2
а
arcsin (-a)=-arcsin a

-а

-arcsin

Арксинус и решение уравнений sin t=a.

t=a.


1) IаI>1

Нет точек пересечения с окружностью.
Уравнение не имеет решений.

t=a.


2) IаI=1

sin t=1
t=П/2+2Пk


sin t=-1
t=-П/2+2Пk

Частный случай.

t=a.


3) а=0

t=Пk



Частный случай.

t=a.


4) IаI

t=(-1)karcsin a+Пk

или

а

[0;П ], косинус которого равен а

а
arccos (-a)=-П-arccos a

-а

П-arccos a
Арккосинус и

окружностью.
Уравнение не имеет решений.

Арккосинус и решение уравнений соs t=a.

и решение уравнений соs t=a.

уравнений соs t=a.

симметричные относительно Оx могут быть записаны:

t=±arccos a+2Пk

или


а
Арккосинус и решение уравнений

которого равен а


arctg a
а
П/2
- П/2
arctg (-a)=-arctg a
-а


-arctg a
Арктангенс и решение

t=a.

arctg a
а
a – любое число.

Частных случаев нет.
t=arctg a+Пk.

которого равен а
-а
arcctg a
arcctg (-a)=П-arcсtg a
а


П-arcctg a
Арккотангенс и решение уравнений

случаев нет.
t=arcctg a+Пk.

Арккотангенс и решение уравнений сtg t=a.

Это частный вид
уравнения cos t=a
a=0

Разделим обе части на 4.

О:

t

t

ошибка.

простейшему.

Разделим обе части на 4.
О:
t
Примеры уравнений.

a=0
Примеры уравнений.

,

Примеры уравнений.

вид.
Решение удобнее разбить на два.
Примеры уравнений.