Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение текстовых задач с экономическим содержанием
Содержание
- 1. Решение текстовых задач с экономическим содержанием
- 2. Задачи на вычисление сложных процентов Процент – одна
- 3. Метод сложных процентов Наиболее часто проценты применяются при
- 4. Транснациональная компания «Amoco inc.» решила провести недружественное
- 5. Оля хочет взять в кредит 100 000
- 6. Вкладчик внёс некоторую сумму в Сбербанк под
- 7. Вкладчик внёс некоторую сумму в Сбербанк под
- 8. 31 декабря 2013 года Сергей взял в
- 9. Алгебраическая модель задачи:((9930000·1,1 – х)·1,1 – х)·1,1
- 10. х
- 11. Алгебраическая модель задачи:
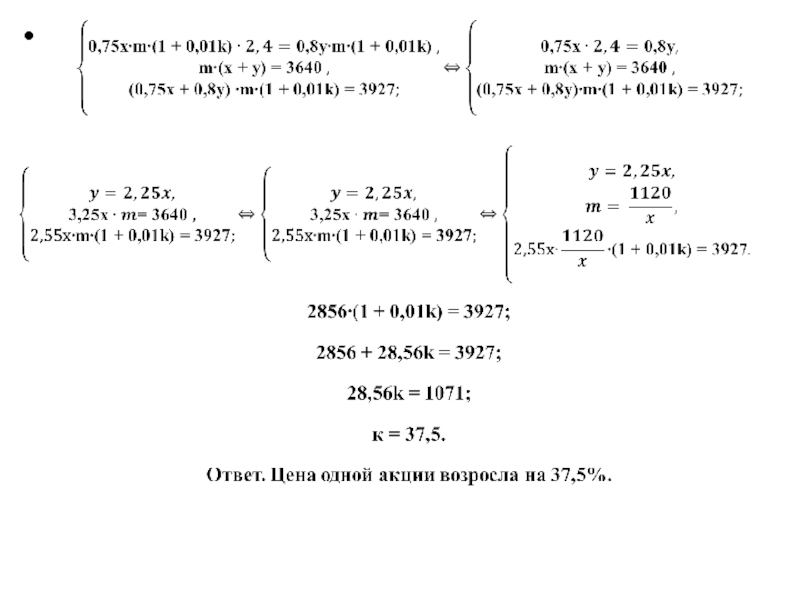
- 12. Два брокера купили акции одного достоинства на
- 13. Слайд 13
- 14. В январе 2000 года ставка по депозитам
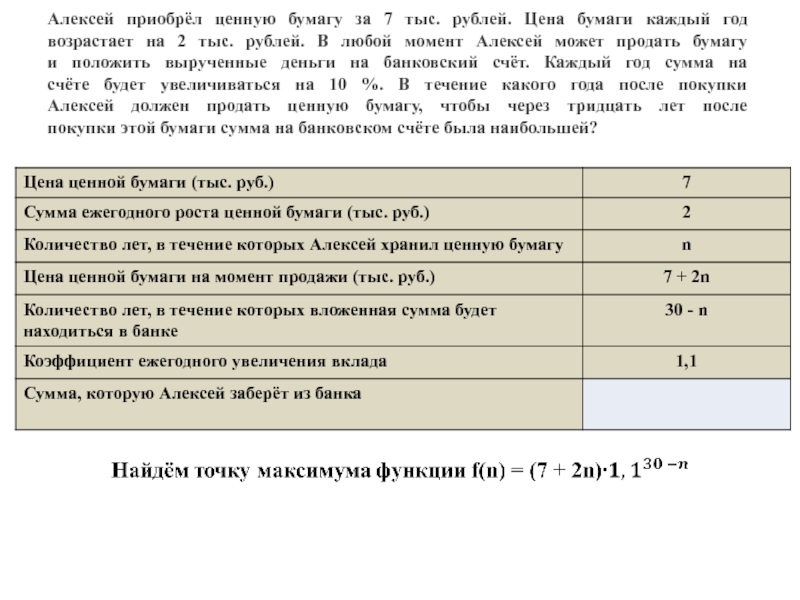
- 15. Алексей приобрёл ценную бумагу за 7 тыс.
- 16. Слайд 16
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Решение текстовых задач с экономическим содержанием
Выполнила:
Генералова Елена Григорьевна,
учитель математики высшей
квалификационной категории
2015 г.Слайд 2Задачи на вычисление сложных процентов
Процент – одна из самых трудных
тем для школьников. Это можно объяснить, в частности, тем, что
понятие процента не является математическим, а относится к экономическим и производственным категориям.Задачи на вычисление сложных процентов имеют особое экономическое содержание, посредством которого определяется уровень риска в процессе принятия решений по оптимизации производства; определению направления вложения ресурсов и т.д.
Только войдя в курс дела, привыкнув к новым словам, ученик может понять, почему получается такое несоответствие: если число x увеличить на число y, а затем полученный результат уменьшить на y, то снова получится x, но, если число x увеличить на 10 %, а затем полученный результат уменьшить на 10 %, то получится не x, а 0,99x.
Слайд 3Метод сложных процентов
Наиболее часто проценты применяются при финансовых расчетах (банковское
дело, доходы от облигаций госзаймов, вкладов в сберегательные банки и
т.п.), а также при учете роста хозяйственной продукции, выполнения производственных планов, роста народонаселения и т.д.При финансовых расчетах число, показывающее, сколько процентов дохода в установленный срок (зачастую в год) приносит та или иная сумма, называется процентной таксой (ставкой), а сама сумма дохода – процентными деньгами. Для расчета процентных денег служат формулы простых и сложных процентов.
Если проценты начисляются по отношению к исходной сумме, то такой метод называется методом простых процентов.
Если проценты начисляются по отношению к величине, включающей первоначальную сумму и проценты, начисленные за прошедший период, то такой метод называется методом сложных процентов.
Слайд 4Транснациональная компания «Amoco inc.» решила провести недружественное поглощение компании «First Aluminum
Company» (FAC) путем скупки акций миноритарных акционеров. Известно, что «Amoco inc.»
было сделано три предложения владельцам акций FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3, а общее количество приобретенных «Amoco inc.» акций поглощаемой компании увеличивалось на 20%. Определите величину третьего предложения и общее количество скупленных акций «First Aluminum Company», если начальное предложение составило $27 за одну акцию, а количество акций, выкупленных по второй цене, — 15 тысяч.
Ответ. Общее количество купленных акций 45.5 тысяч, величина третьего предложения 48 долларов за акцию.
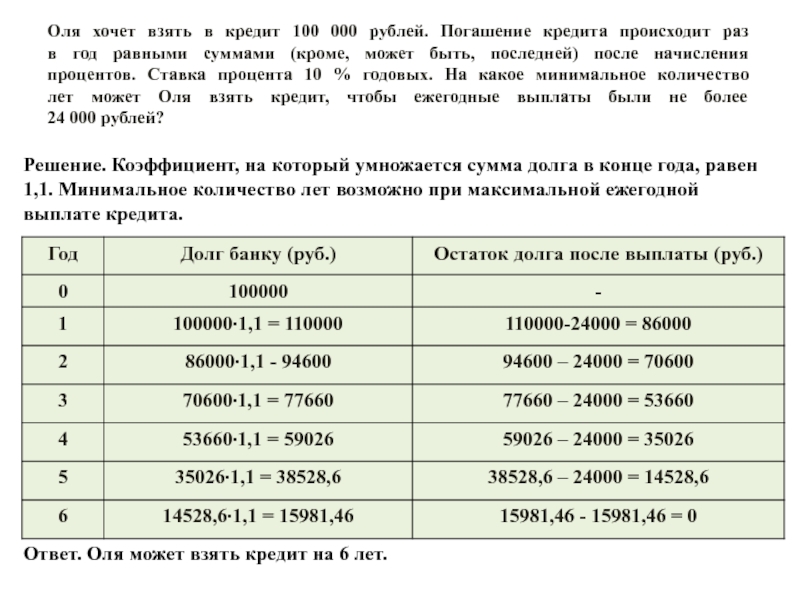
Слайд 5Оля хочет взять в кредит 100 000 рублей. Погашение кредита
происходит раз в год равными суммами (кроме, может быть, последней) после
начисления процентов. Ставка процента 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 24 000 рублей?Решение. Коэффициент, на который умножается сумма долга в конце года, равен 1,1. Минимальное количество лет возможно при максимальной ежегодной выплате кредита.
Ответ. Оля может взять кредит на 6 лет.
Слайд 6Вкладчик внёс некоторую сумму в Сбербанк под определённый процент годовых.
Через год он взял половину получившейся суммы и переложил её
в коммерческий банк, процент годовых которого в 32 раза выше, чем в Сбербанке. Ещё через год сумма вкладчика в коммерческом банке превысила вложенную туда первоначальную сумму на 4%. Каков процент годовых в Сбербанке?Решение. Пусть сумма вклада в Сбербанк а рублей под q% годовых.
Алгебраическая модель задачи:
0,5∙a∙(1 + 0,01q)∙(1 + 0,32q) = 0,5∙a∙(1 + 0,01q)∙1,04.
1 + 0,32q = 1,04;
q = 0,125
Ответ. Вклад в Сбербанк был вложен под 0,125% годовых.
Слайд 7Вкладчик внёс некоторую сумму в Сбербанк под определённый процент годовых.
Через год он взял половину получившейся суммы и переложил её
в коммерческий банк, процент годовых которого в 32 раза выше, чем в Сбербанке. Ещё через год сумма вкладчика в коммерческом банке превысила вложенную туда первоначальную сумму на 4%. Каков процент годовых в Сбербанке?2-й способ. Условие можно свести к более простому.
Вкладчик некоторую сумму положил в коммерческий банк, процент годовых которого в 32 раза выше, чем в Сбербанке. Через год сумма вкладчика в коммерческом банке превысила вложенную туда первоначальную сумму на 4%. Каков процент годовых в Сбербанке?
Решение.
Процент годовых в коммерческом банке равен 4.
А в Сбербанке в 32 раза меньше, т.е. 4 : 32 = 0,125
Ответ. Вклад в сбербанк был вложен под 0,125% годовых.
Слайд 831 декабря 2013 года Сергей взял в банке 9 930
000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая:
31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами? Решение. Пусть ежегодный платёж равен х рублей.
Слайд 9Алгебраическая модель задачи:
((9930000·1,1 – х)·1,1 – х)·1,1 – х =
0.
(9930000·1,1·1,1 – 1,1х – х)·1,1 – х = 0;
9930000·1,1·1,1·1,1 –
2,1х·1,1 – х = 0;9930000·1,331 – 3,31х = 0;
х = 3993000.
Ответ. Сумма ежегодного платежа должна быть
3993000 рублей.