Решение уравнений

МОУ-СОШ №43 г.Белгорода)
Трифонова Наталья Владимировна – учитель математики (I квалификационная

МБОУ СОШ №43 г. Белгорода

монотонности функции
«Ищи квадратный трехчлен»

частью решения.
Для получения уравнения-следствия достаточно посмотреть на заданное уравнение как

Пример:

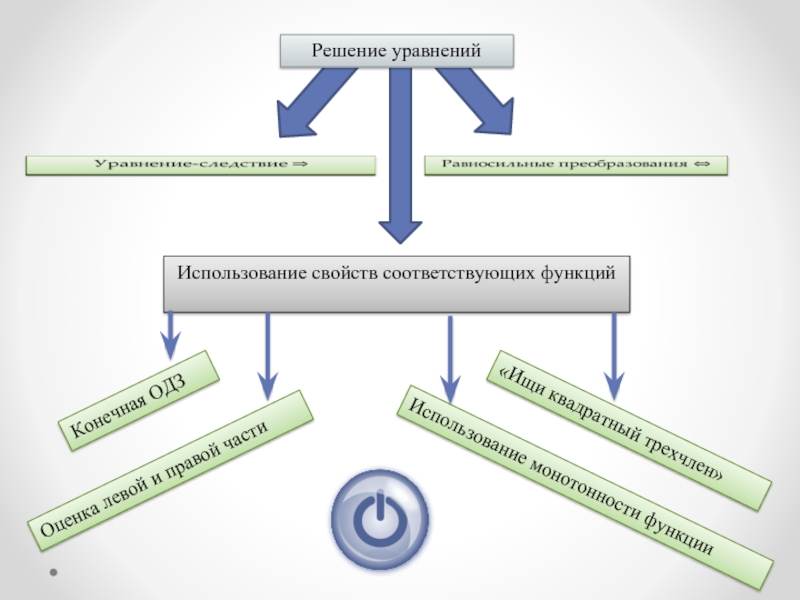
именно: если в верном числовом равенстве перенести член из одной

Если числа равны то и квадраты равны.

Если оби части верного неравенства разделить на число 2≠0, то равенство не нарушится.

Раскрывая скобки и перенося все члены в одну сторону, мы снова получаем верное равенство, откуда находим корни неполного квадратного уравнения

Проверка:
При х=0
получаем неверное равенство (-1=1)
При х=3
получаем верное равенство (1=1)

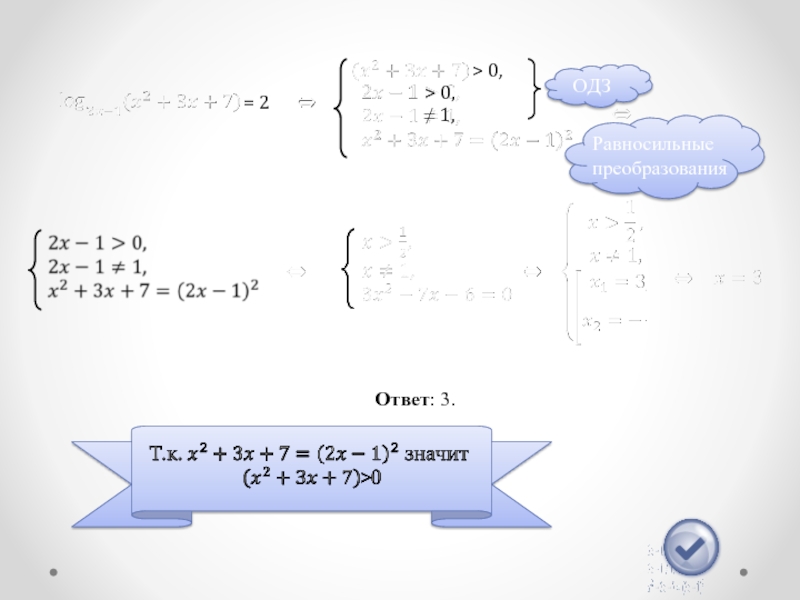
Поскольку для решения уравнения мы использовали уравнение-следствие, то в решение входит также проверка найденных корней подстановкой в исходное уравнение

Ответ: 3

Если числа равны то и квадраты равны.

прямые и обратные преобразования
Пример:

из конечного числа значений, то для решения достаточно проверить все

У некоторых уравнений область определения состоит только из конечного числа
точек. Для решения таких уравнений достаточно проверить, не являются ли найденные числа из области определения уравнения корнями этого уравнения.

Пример:

нулю тогда и только тогда, когда все функции одновременно равны

Пример:

Пример:

тогда, когда все функции одновременно равны нулю.

корней это уравнение не имеет
x
α
β
x0
a
y=a
y=f(x)
0
x
α
β
x0
a
y=a
y=f(x)
0
y=g(x)
Если в уравнении
f(x)=a
функция f(x) возрастает (убывает)
на

то это уравнение может

иметь не более чем один корень на этом промежутке

y

Теорема 1

y

Теорема 2

Если в уравнении f(x)=g(x) функция f(x) возрастает

на некотором промежутке,

а функция g(x) убывает на

то это уравнение

этом промежутке (или наоборот),

может иметь не более чем один корень на этом
промежутке

Пример:

Пример:

корней это уравнение не имеет
Ответ: х=1.

корней это уравнение не имеет
Ответ: х=2

какой-либо функции)
Решение:

задач в таблицах»;
Е.П.Нелин Методы решения алгебраических задач (приложение к учебному

задач в таблицах»;
Office.com – кнопки для навигации по сайту.