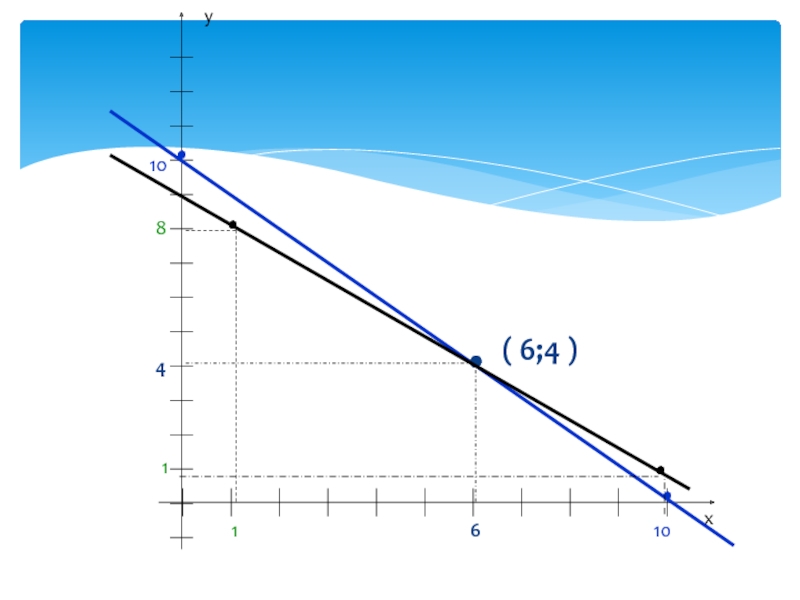
скобка означает, что все уравнения должны выполняться одновременно
Каждая пара значений
переменных, которая одновременно является решением всех уравнений системы, называется решением системыРешением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Решить систему уравнений - это значит найти все её решения или установить, что их нет
Система уравнений