Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
События, вероятность, статистическая обработка данных
Содержание
- 1. События, вероятность, статистическая обработка данных
- 2. Элементы комбинаторики, статистики теории вероятностейКомбинаторика: Примеры решения
- 3. Учащиеся должны уметь:Извлекать информацию, представленную в таблицах,
- 4. Правило умножения. Дерево вариантовНа завтрак Вова может
- 5. Правило умножения. Дерево вариантовОтветить на этот вопрос
- 6. Правило умножения. Дерево вариантовДля того, чтобы найти
- 7. Дерево вариантовСколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9 ?Ответ:15
- 8. факториалПроизведение первых подряд идущих n натуральных чиселобозначают
- 9. перестановкиN различным элементам можно присвоить номера от
- 10. перестановкиРешите уравнение:n!=7(n-1)! n!\ (n-1)!=7 n=7Вычислите:
- 11. Выбор нескольких элементов. Сочетания.
- 12. Выбор нескольких элементов. Сочетания.В чемпионате участвовало 7
- 13. Выбор нескольких элементов. СочетанияВ классе 27 учеников,
- 14. Сочетания.Понятие «выбор» означает сам процесс, а «выборка»-это тот конкретный объект, который мы выбрали
- 15. Выбор нескольких элементов. СочетанияЧисло способов, при которых
- 16. Сочетания.Определение: число всех выборов k элементов из
- 17. Сочетания.
- 18. Сочетания.Для чисел Сkn есть имеется очень красивый
- 19. Скачать презентанцию
Элементы комбинаторики, статистики теории вероятностейКомбинаторика: Примеры решения комбинаторных задач: перебор вариантов, правило умножения, дерево вариантов факториал, перестановкиСтатистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результаты измерений. Понятие о статистическом
Слайды и текст этой презентации
Слайд 1
События. Вероятности. Статистическая обработка данных.
7-9 класс
Учитель математики МКОУ Могутовская
СОШ Акчувашева Т.Н.
Слайд 2Элементы комбинаторики, статистики теории вероятностей
Комбинаторика: Примеры решения комбинаторных задач: перебор
вариантов, правило умножения, дерево вариантов факториал, перестановки
Статистические данные. Представление данных
в виде таблиц, диаграмм, графиков. Средние результаты измерений. Понятие о статистическом выводе на основе выборки.Понятие и примеры случайных событий.
3. Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.
Слайд 3Учащиеся должны уметь:
Извлекать информацию, представленную в таблицах, на диаграммах, графиках;
составлять таблицы, строить диаграммы, графики
Решать комбинаторные задачи путем систематического перебора
возможных вариантов, а также с использованием правила умноженияВычислять средние значения результатов измерений
Находить частоту события, используя собственные наблюдения и готовые статистические данные
Находить вероятности случайных событий в простейших случаях
Слайд 4Правило умножения. Дерево вариантов
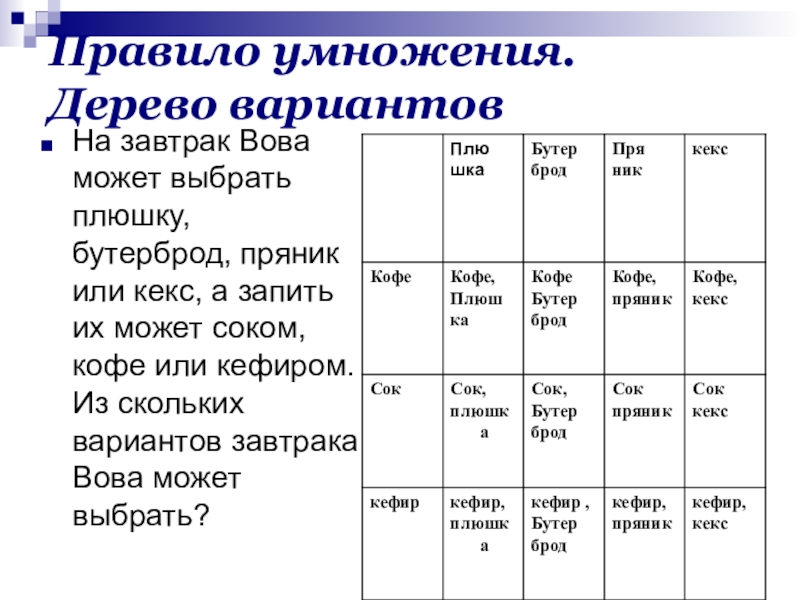
На завтрак Вова может выбрать плюшку, бутерброд,
пряник или кекс, а запить их может соком, кофе или
кефиром. Из скольких вариантов завтрака Вова может выбрать?
Слайд 5Правило умножения. Дерево вариантов
Ответить на этот вопрос можно тремя способами
1 способ: простым перебором;
2 способ: с помощью дерева
вариантов;3 способ: по правилу умножения (перестановками)
В таблице 3 строки и четыре столбца, они образуют 12 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоять один из возможных вариантов завтрака и, наоборот, любой вариант завтрака будет записан в одной клетке. Значит, всего вариантов столько же, сколько клеток в таблице. Ответ:12
Слайд 6Правило умножения. Дерево вариантов
Для того, чтобы найти число всех возможных
исходов независимого проведения двух испытаний А и В, следует перемножить
число всех исходов испытания А и число всех исходов испытания В
Слайд 7Дерево вариантов
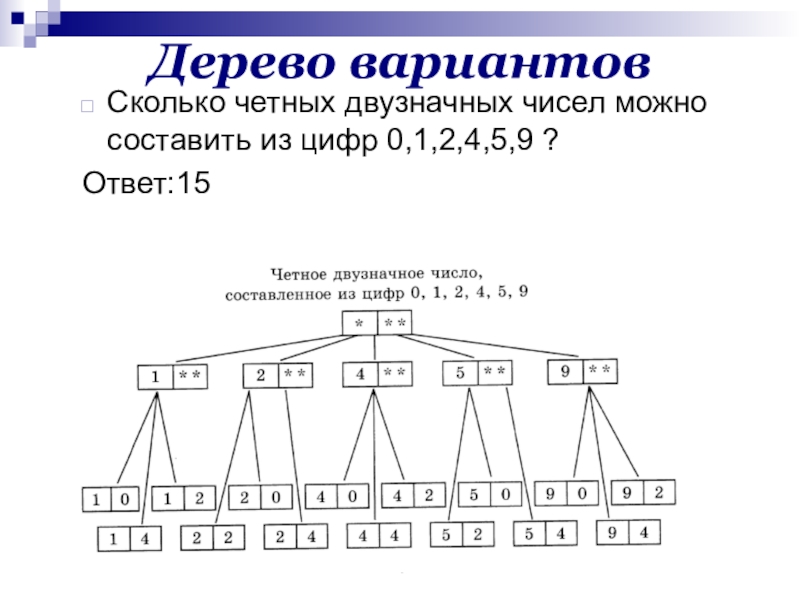
Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9
?
Ответ:15
Слайд 8факториал
Произведение первых подряд идущих n натуральных чисел
обозначают n! Знак n!
Читается как
«эн факториал», что в переводе с английского означает
«состоящий из n множителей»
n! =1*2*3*…*(n-2)(n- 1)n
Например: 6!=1*2*3*4*5*6
Слайд 9перестановки
N различным элементам можно присвоить номера от 1 до n
ровно n! различными способами. Каждый способ нумерации от 1 до
n называют перестановкой данного n-элементного множества.Число перестановок множества из n элементов обозначают Рn
Рn= n!
n
Слайд 12Выбор нескольких элементов. Сочетания.
В чемпионате участвовало 7 команд. Каждая команда
играла один матч с каждой. Сколько всего было встреч?
Так как
никакая команда не играла сама с собой, то клетки по диагонали надо закрасить, тогда в подсчете числа встреч будет участвовать ровно 72-7=7(7-1)=42 клетки. В результате таблица разделилась на две половины, в них результаты встреч дублируются. Поэтому данное выражение делим на два
Слайд 13Выбор нескольких элементов. Сочетания
В классе 27 учеников, из которых нужно
выбрать троих. Сколькими способами это можно сделать, если а) первый
ученик должен решить задачу, второй сходить за мелом, третий идти в столовую дежурить б) им следует спеть хором?В первом случае важен порядок вызова учеников и применимо правило умножения. Один из 27 учеников идет решать задачу. Один из оставшихся 26 идет за мелом, а один из оставшихся 25 будет дежурить в столовой. Получается: 27*36*25=17550
Слайд 14Сочетания.
Понятие «выбор» означает сам процесс, а «выборка»-это тот конкретный объект,
который мы выбрали
Слайд 15Выбор нескольких элементов. Сочетания
Число способов, при которых порядок выбора трех
элементов из 27 не важен, в 3! раз меньше числа
способов, при которых порядок выбора важен 3!=3*2*1=6
Слайд 16Сочетания.
Определение: число всех выборов k элементов из n данных без
учета порядка обозначают Сkn
Для числа сочетаний из n элементов
по k cправедлива формула Сkn=
Слайд 18Сочетания.
Для чисел Сkn есть имеется очень красивый и удобный способ
записи –в виде треугольной таблицы, ее называют треугольником Паскаля
