Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
способы решения квадратных уравнений
Содержание
- 1. способы решения квадратных уравнений
- 2. Человеку, изучающему алгебру, часто полезнее решить одну
- 3. Урок одной задачиРазличные способы решения квадратных уравнений
- 4. Цели: - систематизировать различные способы решения квадратных
- 5. Методы решения квадратных уравнений были известны
- 6. В трудах древнегреческого математика Евклида и многих математиков древности квадратные уравнения решались геометрическим способомЕвклид
- 7. Для решения квадратных уравнений поступали следующим образом.х
- 8. Аль - ХорезмиВ трактате «Китаб аль-джебр валь-мукабала»
- 9. Так решал эту же задачу ал-Хорезми в
- 10. Древнегреческий математик Диофант3 век нашей эрыПусть сумма
- 11. М. Штифель (1487-1567)Общее правило решения квадратных уравнений,
- 12. Франсуа Виет(1540-1603)Именно этим французским математиком впервые были
- 13. . С 1591 г. мы пользуемся формулами
- 14. ах2 + bх + с = 0
- 15. Формулировка т. Виета. Обратная т. Виета. Зависимость знаков корней квадратного уравнения, от коэффициентов.
- 16. Если второй коэффициент уравнения чётный , можно использовать иную формулу – формулу чётных коэффициентов.
- 17. Квадратные уравнения можно решить, используя свойства «суммы
- 18. В учебнике мы встречаем задания , где
- 19. Задача №1Известно, что учет населения проводился в
- 20. Задача №2 На основе статистических данных можно
- 21. Кислотные осадки разрушают сооружения из мрамора и
- 22. Слайд 22
- 23. Подведение итоговНаш урок подходит к концу, подумайте
- 24. « Теория без практики мертва и бесплодна,
- 25. До новых встреч!Желаю творческих успехов
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ст. Вёшенская
МОУ ВСШ
им. М.И. Платова
учитель математики
Калинина Елена Владимировна
2008-2009 уч.
год
Слайд 2Человеку, изучающему алгебру, часто полезнее решить одну задачу тремя различными
способами, чем решать три-четыре различные задачи.
Решая одну задачу различными способами,
можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.У.У. Сойер
Слайд 4Цели:
- систематизировать различные способы решения квадратных уравнений, дать представление
учащимся о важных вехах истории развития математики;
-обучать поискам нескольких
способов решения одной задачи и умению выбирать из них наиболее оригинальный , оптимальный;- развивать навыки работы с дополнительной литературой, историческим материалом, формировать интерес к изучению математики
Слайд 5 Методы решения квадратных уравнений были известны ещё в давние
времена. Их умели решать вавилоняне ( около 2
тыс. лет до н.э.). Об этом свидетельствуют найденные клинописные тексты задач с решениями в виде уравнений.Также они излагались в вавилонских рукописях царя Хаммурапи.
Находки древности
Слайд 6В трудах древнегреческого математика Евклида и многих математиков древности квадратные
уравнения решались геометрическим способом
Евклид
Слайд 7Для решения квадратных уравнений
поступали следующим образом.
х 2+10х =39
Пусть АВ
=х, ВС=5, (10:2)
АС=АВ+ВС
Если
Число 3 является корнем уравнения, ведь отрицательных
чисел тогда не зналиСлайд 8Аль - Хорезми
В трактате «Китаб аль-джебр валь-мукабала» хорезмский математик разъяснил
приёмы решения уравнений ах2 = вх, ах2 = с и
т.д.( буквами а, в, с обозначены лишь положительные числа) и отыскивает лишь положительные корни
Слайд 9Так решал эту же задачу ал-Хорезми в 825году
Строим квадрат
со стороной х и на его сторонах – 4 прямоугольника
высотойВ углах фигуры построим 4 квадрата со стороной . Подсчитаем площадь получившегося большого квадрата:
По условию
Значит его сторона равна 8, тогда х=3
(Ал-Хорезми не признавал отрицательных чисел).
х 2+10х =39
Слайд 10Древнегреческий математик Диофант
3 век нашей эры
Пусть сумма двух чисел 20,
а произведение 96. Предположим , что их разность 2z.
Большее из
искомых чисел (z+10) , а меньшее (-10 –z)Таким образом (10+z)(10-z)=96
z=2
Следовательно, большее число равно 12, а меньшее8
Не каждое уравнение
можно решить
данным методом
Слайд 11М. Штифель (1487-1567)
Общее правило решения квадратных уравнений, приведённых к виду
х2 +bx = c, было сформулировано немецким математиком Штифелем.
После трудов Рене Декарта и Исаака Ньютона способ решения квадратных уравнений принял современный вид, как для положительных корней, так и для отрицательных.И. Ньютон(1643-1727)
Слайд 12Франсуа Виет(1540-1603)
Именно этим французским математиком впервые были введены буквенные обозначения.
До этого пользовались громоздкими словесными формулировками.
Например: «Квадрат и число
24 равны одиннадцати корням» или x2 + 24 = 11x Формулы, выражающие зависимость корней от его коэффициентов, были выведены Виетом в 1591г.
Слайд 13.
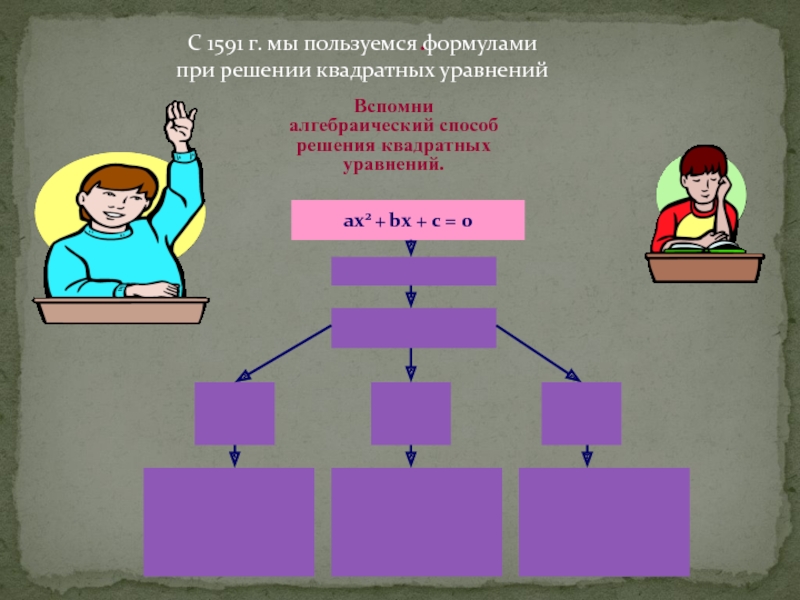
С 1591 г. мы пользуемся формулами
при решении квадратных
уравнений
Вспомни алгебраический способ
решения квадратных уравнений.
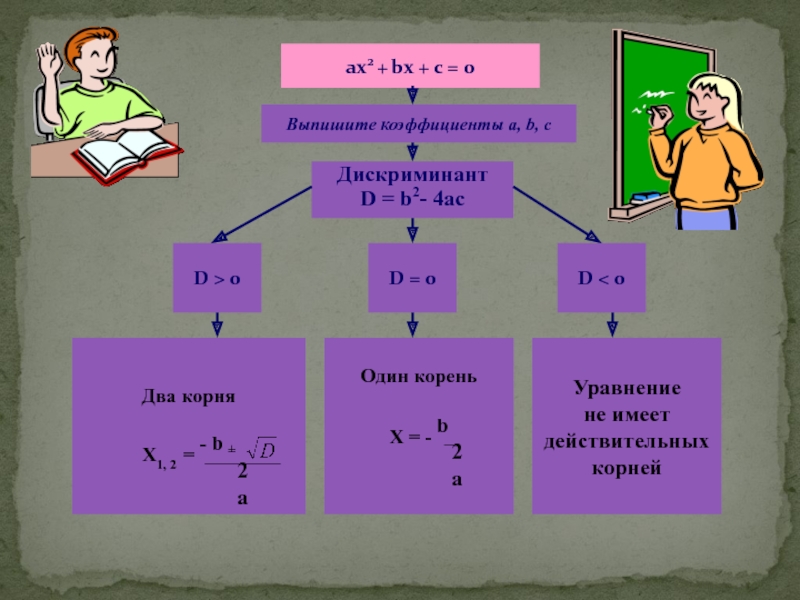
Слайд 14ах2 + bх + с = 0
Выпишите коэффициенты a,
b, c
Дискриминант
D = b2- 4ac
D > 0
D = 0
D
0Два корня
Х1, 2 = - b ±
Один корень
Х = - b
Уравнение
не имеет
действительных
корней
2а
Слайд 15Формулировка т. Виета. Обратная т. Виета. Зависимость знаков корней квадратного
уравнения, от коэффициентов.
Слайд 16Если второй коэффициент уравнения чётный , можно использовать иную формулу
– формулу чётных коэффициентов.
Слайд 17Квадратные уравнения можно решить, используя свойства «суммы коэффициентов»
ах2 + bх
+ с =0
Если в уравнении
то
то
Не каждое уравнение
можно решить
данным методом
Слайд 18В учебнике мы встречаем задания , где четко обозначено ,
как решить квадратное уравнение .
В предложенных задачах вы не только
решите уравнение, но и узнаете интересные факты.Слайд 19Задача №1
Известно, что учет населения проводился в Египте и в
Китае ещё до нашей эры. Решив квадратное уравнение
вы определите,
в каком это было тысячелетии до н.э.Реши задачу разными способами
Слайд 20Задача №2
На основе статистических данных можно выделить регионы с
максимальным сбросом загрязнённых вод: это Краснодарский край и Москва. Сколько
процентов общего количества загрязнённых вод дают эти регионы, вы узнаете решив уравнение.Реши задачу разными способами
Слайд 21Кислотные осадки разрушают сооружения из мрамора и других материалов. Исторические
памятники Греции и Рима , постояв тысячелетия , за последние
годы разрушаются прямо на глазах. «Мировой рекорд» принадлежит одному шотландскому городку , где 10 апреля 1974 г. Выпал дождь , скорее напоминающий столовый уксус , чем воду .Устно решите уравнения , найдите верный ответ и соответствующую ему букву и прочитаете название этого «знаменитого» городаСлайд 23Подведение итогов
Наш урок подходит к концу, подумайте о том с
какой пользой для вас прошёл этот урок, начните свой ответ
с любого из предложений: Я знаю, что ...
Я хорошо знаю, что ...
Я должен знать, что ...
Слайд 24« Теория без практики
мертва и бесплодна,
практика без теории
невозможна и пагубна.
Для теории нужны знания,
для практики, сверх
того, и умение»
На уроке мы рассмотрели различные способы
Решения квадратных уравнений. Квадратные уравнения – это фундамент, на котором покоится алгебра.