Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Старинный способ решения задач на процентное содержание 8 класс
Содержание
- 1. Старинный способ решения задач на процентное содержание 8 класс
- 2. Цели: - выяснить, какие математические
- 3. Задачи: сформировать умения применения в практической деятельности:
- 4. Методы исследования:-изучение различной литературы, связанной с данной
- 5. Задача 1 Торговец продаёт орехи
- 6. 2 способ решения Пусть х кг –
- 7. Задача 2
- 8. 2 способ решенияПусть х л – масса
- 9. Слайд 9
- 10. Задача 3 Имеется две смеси
- 11. 2 способ решенияПусть х л – масса
- 12. Слайд 12
- 13. Задача 4 30
- 14. 2 способ решения Пусть х – масса
- 15. Слайд 15
- 16. Слайд 16
- 17. ЗаключениеРешение задач на проценты имеет большое прикладное
- 18. Литература1. Артеменко А.Р., Задачи на концентрацию и
- 19. Спасибо за внимание
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Муниципальное бюджетное образовательное учреждение «Средняя образовательная школа №14» « Старинный способ решения
задач на процентное содержание»
Слайд 2
Цели:
- выяснить, какие математические способы позволяют быстро
решать задачи на концентрацию, смешивание, сплавление любого числа веществ;
-показать красоту,
сложность и притягательность старинного способа решения задач; необходимость знаний процентных вычислений для решения большого круга задач, показав широту применения процентных расчётов в реальной жизни;
- способствовать интеллектуальному развитию, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной организации и решения практических проблем;
- использование программной среды для представления математических задач.
Слайд 3
Задачи:
сформировать умения применения в практической деятельности:
- производить
процентные вычисления;
- работать с законом сохранения массы;
- обеспечить
усвоение понятий концентрации вещества процентного раствора;- решать задачи на смешивание , сплавление, концентрацию то есть задачи на процентное содержание или концентрацию;
- обобщить полученные знания при решении задач на процентное содержание;
- оценивать свой потенциал с точки зрения перспективы.
Слайд 4
Методы исследования:
-изучение различной литературы, связанной с данной темой;
-сравнение и
сопоставление полученных данных с теоретическими выводами:
- анализ и обобщение результатов
Предмет
исследования:процесс применения математических способов при решении задач на проценты.
Объект исследования:
старинный способ решения задач на концентрацию, смешивание, сплавление.
Гипотеза:
при ознакомлении сверстников со старинным способом решения задач на концентрацию, смешивание, сплавление у них появится больше шансов успешно сдать ГИА.
Слайд 5Задача 1
Торговец продаёт орехи двух сортов: одни
по цене 90 центов, другие по 60 центов за килограмм.
Он хочет получить 50 кг смеси по 72 цента за килограмм. Сколько для этого потребуется орехов каждого сорта?Решение:
50 : (12 + 18) =1,6 (кг) – 1 часть.
1,6× 12 = 20 (кг) – по 90 центов.
1,6× 18 = 30 (кг) – по 60 центов.
Ответ: 20 кг и 30 кг.
90 12
72
60 18
Слайд 62 способ решения
Пусть х кг – масса первого сорта,
тогда
(50 – х) кг – масса второго сорта
0,9х кг –
масса орехов по 90 центов0,6 кг – масса орехов по 60 центов
0,75 * 50 кг – масса орехов по 72 цента
Составляем уравнение:
0,9х + 0,6(50 – х) = 0,75 * 50
0,9х + 30 – 0,6х = 36
0,3х = 6
Х = 6 : 0,3
Х = 20 (кг) – по 90 центов
50-20 = 30 (кг) – по 60 центов
Ответ: 20 и 30 кг
Слайд 7Задача 2
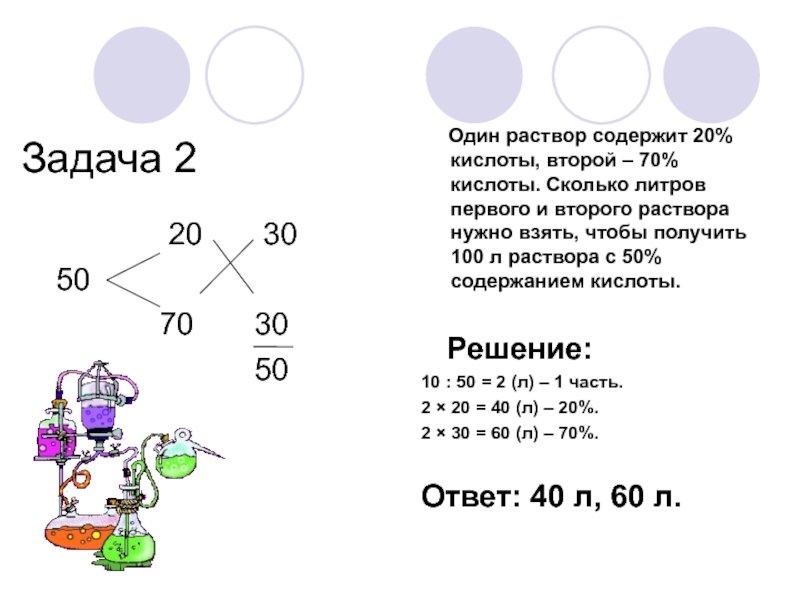
20
30
50
70 3050
Один раствор содержит 20% кислоты, второй – 70% кислоты. Сколько литров первого и второго раствора нужно взять, чтобы получить 100 л раствора с 50% содержанием кислоты.
Решение:
10 : 50 = 2 (л) – 1 часть.
2 × 20 = 40 (л) – 20%.
2 × 30 = 60 (л) – 70%.
Ответ: 40 л, 60 л.
Слайд 82 способ решения
Пусть х л – масса первого раствора,
тогда (100
– х) л – масса второго раствора
0,2х л –
масса кислоты в первом растворе 0,7 (100 – х) л – масса кислоты во втором растворе
100 * 0,5 л – масса кислоты в новом растворе
Составляем уравнение:
0,2х + 0,7 (100 – х) = 100 * 0,5
0,2х + 70 – 0,7х = 50
0,5х = 20
Х = 40 (л) – масса первого раствора
100 – 40 = 60 (л) – масса второго раствора
Ответ: 40 л и 60 л
Слайд 10Задача 3
Имеется две смеси апельсинового и ананасового
соков. Первая смесь содержит 40% апельсинового сока, вторая 80% .
Сливаются р (л) первой смеси и q (л) второй, в результате получается 20 л смеси, содержащей 70% апельсинового сока. Определить p и q.Решение:
20 : (10 + 30) = 0,5 (л) – 1 часть.
р = 10 × 0,5 = 5 (л)
q = 30 × 0,5 = 15 (л)
Ответ: р = 5 л, q = 15 л
40 10
70
80 30
Слайд 112 способ решения
Пусть х л – масса первой смеси
тогда (20
– х) л – масса второй смеси
0,4х л – апельсинового
сока0,8 (20 – х) л – ананасового сока
0,7 * 20 л – смесь апельсинового сока
Составляем уравнение:
0,4х + 0,8 (20 – х) = 0,7 * 20
-0,4х + 16 = 14
0,4х = 2
Х = 5 (л) – апельсиновый сок
20 – 6 = 15 (л) – ананасовый сок
Ответ: р = 5 л , q = 15 л
Слайд 13Задача 4
30 15
40
55 10
Имеются два сплава с разным содержанием золота. В первом сплаве содержится 30%, а во втором – 55% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить новый сплав, содержащий 40% золота? Решение:
15:10 = 3:2
Ответ: 3:2
Слайд 142 способ решения
Пусть х – масса первого сплава
у – масса второго сплава
0,3х –
масса золота в первом сплаве0,55у – масса золота во втором сплаве
0,4 (х + у) – масса золота в новом сплаве
Составляем уравнение:
0,3х + 0,55у = 0,4 (х + у)
0,55у – 0,4у = 0,4х – 0,3х
0,15у = 0,1х
Х : 4 = 3 : 2
Ответ: 3 : 2
Слайд 17Заключение
Решение задач на проценты имеет большое прикладное значение в финансовой,
промышленной, медицинской, социальной сторонах повседневной жизни каждого человека.
Математический аппарат процентов
применяется к решению повседневных, бытовых проблем каждого человека, вопросов рыночной экономики.Значение теории процентов важно и полезно для общего развития человека, повышения общей математической культуры, позволяет получить подготовку для сдачи ЕГЭ.
В данной работе мы рассмотрели применении истории процентов при решении задач на процентное содержание и концентрацию ,смешивание, сплавление.
В дальнейшем мы думаем продолжать изучение этой темы и рассмотреть решения таких задач с помощью уравнений и систем уравнений.
Слайд 18Литература
1. Артеменко А.Р., Задачи на концентрацию и процентное содержание //
Математика в школе - 1994. - № 4. - с.
15 - 18.2. Барабанов О.О. Задачи на проценты как проблемы словообразования // Математика в школе. - 2003. - № 5. – с. 50 – 59.
3. Виленкин Н.Л. За страницами учебника математики. – М: Просвещение, 1989. – с. 73.
4. Глейзер Г.И. История математики в школе (4 – 6 кл): пособие для учителей. – М.: Просвещение, 1981.
5. Олехник С.Н., Нестеренко Ю.В., Потапов М.К. Старинные занимательные задачи – М.: Наука, 1988, 160 с.
6. Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику – М.: Наука, 1989. – 238 с.
7. Соломатин О.Д. Старинный способ решения задач на сплавы и смеси // Математика в школе. – 1997. - № 1. – с. 12 – 13.
8. Шорина С.П. Обоснование старинного способа решения задач на смеси // Математика в школе. – 1998. - № 6. – с. 77.
9. Сайт в интернете: Способы решения задач.
10. Сайт в интернете: Задачи древних в современном мире.
11. Сайт в интернете: Методика использования исторических задач.