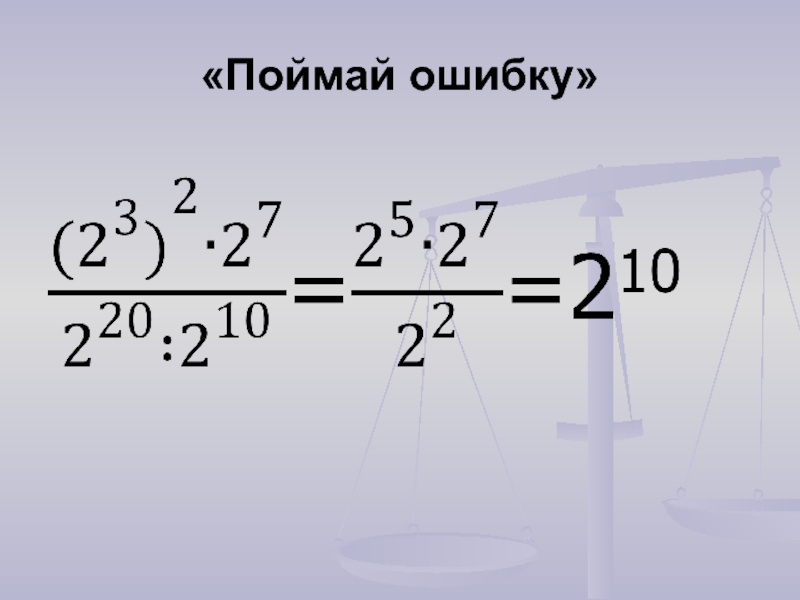Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Степень с натуральным показателем и ее свойства
Содержание
- 1. Степень с натуральным показателем и ее свойства
- 2. Цель урока: повторение, обобщение и систематизация знаний
- 3. Эпиграф урока:«Пусть кто-нибудь попробует вычеркнуть из математики
- 4. Проверка теоретической частиЕсли показатель четное число, то
- 5. При умножении степеней с одинаковыми основаниями надо основание оставить тем же, а показатели степеней сложить.
- 6. При делении степеней с одинаковыми
- 7. При возведении степени в степень надо основание оставить прежним, а показатели степеней перемножить.
- 8. Устный счёт1.Упростите выражение: а6∙а7; (3х)2; у17:у5; х2∙х8:х; (хуz)3; (b+1)3∙(b+1)4.
- 9. Устный счёт
- 10. Устный счёт3. Представьте в виде степени с
- 11. Устный счёт
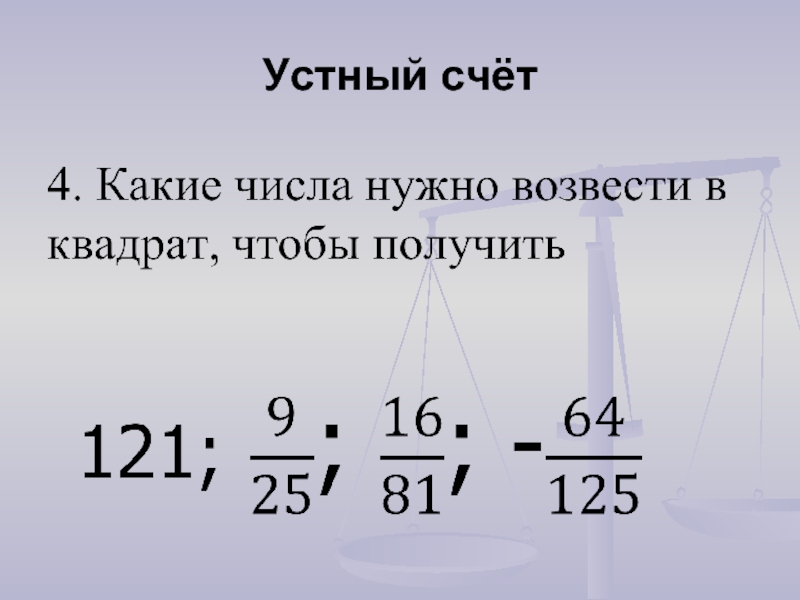
- 12. Устный счёт5. Какие числа нужно возвести в
- 13. «Поймай ошибку»
- 14. Вычислительная паузаа) Представьте выражение в виде степени с основанием 7
- 15. Вычислите 311 • 27 96
- 16. Решите уравнения 78 : х = 75
- 17. Физкультминуткаа) неравенства – «наклон влево, наклон вправо»(-7)11
- 18. Физкультминуткаб) упражнения для глаз на расслабление(загадки о
- 19. ФизкультминуткаНи угла, ни стороны,А родня – одни
- 20. Самостоятельная работаЗаполните пропуски, чтобы равенство было верным.1.
- 21. 1. (y2)2 ∙ (у2)3= y10.
- 22. ТЕСТ Выпишите ответы на вопросы теста в тетрадь и прочитайте шифр.
- 23. Ответы к тестуВариант 1
- 24. оценка10-9 правильных ответов – «5»8-7 правильных ответов
- 25. Это интересноСИМОН СТЕВИН (1548- 1620) – нидерландский
- 26. Это интересно, , РЕНЕ ДЕКАРТ (1596-1650) –
- 27. Работа в парахНайдите верные неравенства. Из соответствующих
- 28. Слайд 28
- 29. Известный архитектор Осип Бове
- 30. РефлексияВ карте самооценки оцените понравился ли урок, свое настроение в конце урока в виде смайлика.
- 31. Домашнее заданиеДомашняя контрольная работа, стр. 97, вариант
- 32. Скачать презентанцию
Цель урока: повторение, обобщение и систематизация знаний по теме; создание условий контроля (взаимоконтроля) усвоения знаний и умений.
Слайды и текст этой презентации
Слайд 2Цель урока:
повторение, обобщение и систематизация знаний по теме; создание
условий контроля (взаимоконтроля) усвоения знаний и умений.
Слайд 3Эпиграф урока:
«Пусть
кто-нибудь попробует вычеркнуть
из математики степени, и он
увидит,
что без них далеко не уедешь».Слайд 4Проверка теоретической части
Если показатель четное число, то значение степени всегда
положительное.
Если показатель нечетное число, то значение степени совпадает
со знаком
основания степени.Слайд 5
При умножении степеней с одинаковыми основаниями надо основание оставить тем
же, а показатели степеней сложить.
Слайд 6
При делении степеней с одинаковыми показателями надо основание
оставить тем же, а из показателя делимого вычесть показатель делителя.
Слайд 7
При возведении степени в степень надо основание оставить прежним, а
показатели степеней перемножить.
Слайд 17Физкультминутка
а) неравенства – «наклон влево, наклон вправо»
(-7)11 -(-8)15
(-7)12
-718 (-4)10 -95
Слайд 18Физкультминутка
б) упражнения для глаз на расслабление
(загадки о геометрических фигурах –
нарисовать контур фигуры глазами)
Три вершины тут видны,
Три угла, три стороны,
-Ну, пожалуй, и довольно! –
Что ты видишь? - ...
Слайд 19Физкультминутка
Ни угла, ни стороны,
А родня – одни блины.
Эта странная фигура,
Ну,
совсем миниатюра!
И на маленький листочек
Мы поставим сотни
Слайд 20Самостоятельная работа
Заполните пропуски, чтобы равенство было
верным.
1. (y2)2 ∙ (…)3=
y10. 2. (…)2 ∙
c3= c13.3. b2 ∙ (…)3= -27b11. 4. (…)2 ∙ a18= a24.
5. (…)4 : a8= a4.
Слайд 211. (y2)2 ∙ (у2)3= y10.
2. (c5)2 ∙ c3= c13.
3. b2
∙ (-3b3)3= -27b11. 4. (a3)2 ∙ a18= a24. 5. (a3)4 : a8= a4.
Самостоятельная работа
Слайд 24оценка
10-9 правильных ответов – «5»
8-7 правильных ответов – «4»
6-4 правильных
ответов – «3»
3-0 правильных ответов – «2»
Слайд 25Это интересно
СИМОН СТЕВИН (1548- 1620) –
нидерландский математик и инженер.
Он
ввёл в употребление десятичные дроби
и отрицательные корни
уравнений.
В конце
16 века степени обозначал в скобках после числа:
Н-р, запись 3(3)+5(2) обозначала
33 + 52
современное обозначение для степеней.
Слайд 26Это интересно
,
,
РЕНЕ ДЕКАРТ (1596-1650) – французский философ и
математик.
Он ввёл в начале 17 века координатную прямую, систему
координат, удобное обозначение:x, y, z – для неизвестных,
a,b,c – для коэффициентов, современное обозначение степеней.
Слайд 27Работа в парах
Найдите верные неравенства. Из
соответствующих им букв получите
фамилию
архитектора, по проекту которого в 1825 г.
было построено
здание Большого театра в Москве:
Слайд 30Рефлексия
В карте самооценки оцените понравился ли урок, свое настроение в
конце урока в виде смайлика.
Слайд 31Домашнее задание
Домашняя контрольная работа, стр. 97, вариант 1.
1 уровень: задания
1-3
2 уровень: задания 1-5
3 уровень: задания 1-9.
Теги