Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометриялық теңдеулер мен теңсіздіктер.Қайталау.
Содержание
- 1. Тригонометриялық теңдеулер мен теңсіздіктер.Қайталау.
- 2. Сабақтың мақсаты:Білімділік: Тригонометриялық теңдеулер
- 3. Тригонометриялық теңдеу деп нені айтады?Қарапайым тригонометриялық теңдеу
- 4. Жауабы:Айнымалысы тригонометриялық функция таңбасының ішінде болатын теңдеу
- 5. жҰпПеН жұмыс№ 115(а,в); №113 (ә);
- 6. Түрткі : (притча) Магараджа өзіне министр іздеді.Ол мынадай
- 7. а) 2sin2 x – 3 sin x
- 8. Топпен жұмысА -тобы Б-тобы В-тобы С-тобы Д-тобы
- 9. А - тобы:1. α = 300 тең
- 10. B – тобы:1. есептеңдер: а) 1 +
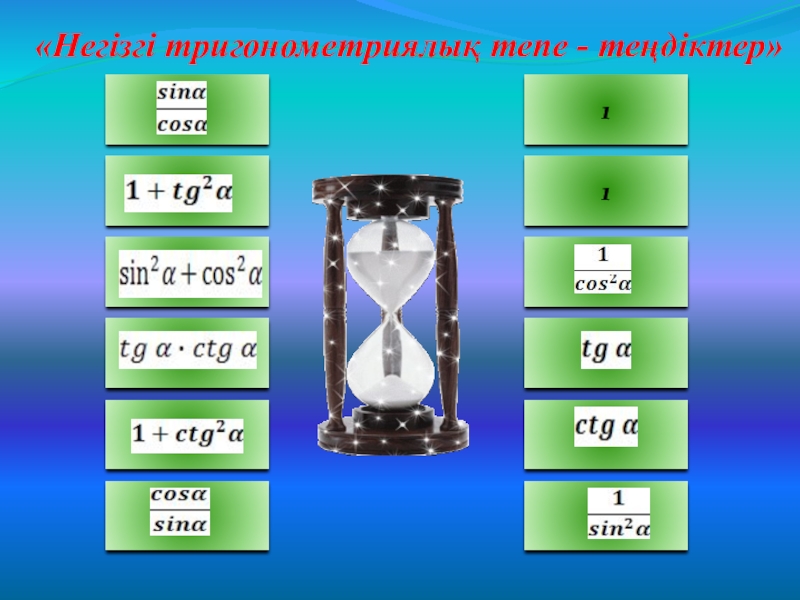
- 11. «Негізгі тригонометриялық тепе - теңдіктер»11
- 12. «Негізгі тригонометриялық тепе - теңдіктер»11
- 13. Математикалық ойын“ЛОТО”
- 14. Математикалық «лото» ойын.
- 15. Сабақты бекіту: Тригонометриялық теңдеулер мен теңсіздіктердің шығару
- 16. Сабақ аяқталды.Рахмет!
- 17. Скачать презентанцию
Сабақтың мақсаты:Білімділік: Тригонометриялық теңдеулер мен теңсіздіктердің шешудің әртүрлі тәсілдерін білу,
Слайды и текст этой презентации
Слайд 2Сабақтың мақсаты:
Білімділік: Тригонометриялық теңдеулер
мен теңсіздіктердің шешудің әртүрлі
тәсілдерін білу,біліктілігін арттыру.
Дамытушылық: Ойлау жүйесін сұрақтарға нақты
жауап беруге, тез шешім
қабылдауға дамытушылығын
арттыру.
Тәрбиелік: Оқушыларды тәрбиелей отырып,
үйрету, ізденімпаздыққа тәрбиелеу.
Слайд 3Тригонометриялық теңдеу деп нені айтады?
Қарапайым тригонометриялық теңдеу дегеніміз не?
Тригонометриялық теңсіздіктерді
шешу дегеніміз не?
y= sin x және y= cos x функциясына
кері функцияны қалай белгілейді және қалай оқиды?Тригонометриялық теңдеулерді шешудің неше жолы бар және атап айту керек?
Ауызша сұрақтар:
Слайд 4Жауабы:
Айнымалысы тригонометриялық функция таңбасының ішінде болатын теңдеу тригонометриялық теңдеу деп
аталады.
sin x = а, , cos x= а ,
tg x= а, ctg x=a түрінде берілген теңдеу қарапайым тригонометриялық теңдеу деп аталады.Берілген теңдеуді тура тепе –теңдікке айналдыратын аргументтің барлық мәндерін табу.
y=arcsin x, y= arccos x.
6 жолы бар:
5.1. Тригонометриялық функциясының бір ғана түрлерімен берілген, алгебралық теңдеулерге келтірілетін тригонометриялық теңдеулер
5.2. Тригонометриялық формулаларды түрлендіру жолымен шешілетін тригонометриялық теңдеулер
5.3. Функциялардың дәрежесін төмендету арқылы шешілетін тригонометриялық теңдеулер.
5.4. Біртектес тригонометриялық теңдеулерді шешу
5.5. Қосымша аргумент енгізу арқылы шығарылатын тригонометриялық теңдеулер.
5.6. Тригонометриялық теңдеулер жүйесін шешу.
Слайд 6 Түрткі : (притча)
Магараджа өзіне министр іздеді.Ол мынадай жарлық салды:,,Егер кімде-кім
құмыра толы сүтпен қабырғамен жүрсе және оны төкпей өтсе,соны министр
қылып аламын”Бірақ ешкім жүре алмады,жолда оларды алаңдатты,сүттерін төгіп алды.Сонда ол былай деп сұрапты:-Сен дауыстар мен атысты естідің бе?-Сені біреу қорқытты ма? Жоқ,тақсыр! Мен тек қана сүтке қарадым. Бөтен нәрсені көрмеу,естімеу – міне осындай дәрежеде назарыңды ӨЗІНДІК ЖҰМЫСТА аудару керек!!!Слайд 7а) 2sin2 x – 3 sin x +1 = 0
sin x = u, 2u2 – 3u +
1 = 0; D = 9 – 8 =1, u1 = 1, u2 = ½sin x=1, x = + 2πn, nϵz. sin x = ½ , x=(-1)n + πn, nϵz
Жауабы: x = + 2πn, x=(-1)n + πn, nϵz
б) 6tg2 x + tg x -1 = 0
tg x = u, 6u2 + u - 1 = 0; D = 1+24 =25, u1 = ⅓ , u2 = -½
tg x= ⅓, x = arctg ⅓ + πn, nϵz. tg x = - ½ , x=arctg(- ½)n + πn, nϵz
ә) cos 5x + cos 3x = 0
2 cos 4x ∙ cos 3x = 0, cos 4x = 0, cos x = 0
4 x = + πn. nϵz. x = , nϵz. cos x = 0, x = + πn. n ϵ z
Слайд 9 А - тобы:
1. α = 300 тең болғанда: sin α
+ cos α өрнегінің мәнін табу керек
Жауабы:
2. 2 sin2
α + cos2 α – 1 – есептеңдер. Жауабы: 2 sin2 α + cos2 α - sin2 α - cos2 α = sin2 α
Б – тобы:
1. Өрнекті ықшамдаңдар:
а) sin α ∙ ctg α = ? Жауабы: sin α ∙ = cos α
б) cos α - sin α ∙ ctg α = ? Жауабы: cos α - sin α ∙ = 0
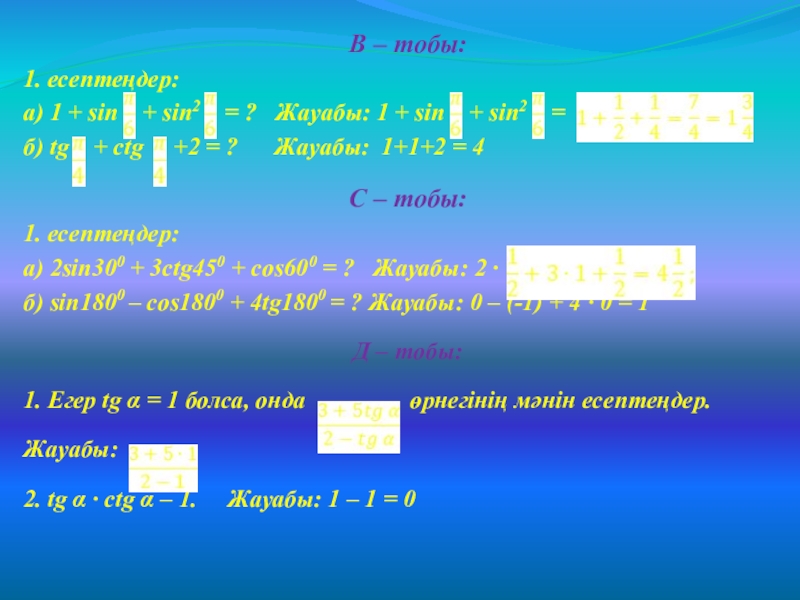
Слайд 10B – тобы:
1. есептеңдер:
а) 1 + sin +
sin2 = ? Жауабы: 1 + sin
+ sin2 =б) tg + ctg +2 = ? Жауабы: 1+1+2 = 4
C – тобы:
1. есептеңдер:
а) 2sin300 + 3ctg450 + cos600 = ? Жауабы: 2 ∙
б) sin1800 – cos1800 + 4tg1800 = ? Жауабы: 0 – (-1) + 4 ∙ 0 = 1
Д – тобы:
1. Егер tg α = 1 болса, онда өрнегінің мәнін есептеңдер.
Жауабы:
2. tg α ∙ ctg α – 1. Жауабы: 1 – 1 = 0
Слайд 15Сабақты бекіту: Тригонометриялық теңдеулер мен теңсіздіктердің шығару
жолдарын бекіту.
Үйге тапсырма: Қайталау
Бағалау және қорытындылау: Бағаланады