Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между плоскостями
Содержание
- 1. Угол между плоскостями
- 2. Данная тема актуальна, так как подобные
- 3. Аргументы1. Определение куба.2. Определение правильной призмы.3. Свойства
- 4. Задача. В кубе найти косинус угла между
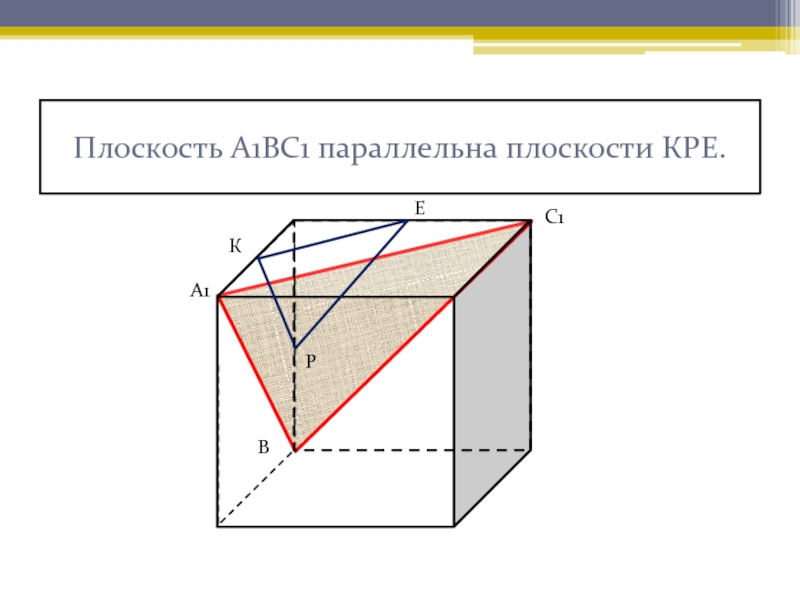
- 5. Плоскость А1ВС1 параллельна плоскости КРЕ.КЕРА1ВС1
- 6. Плоскость А1ВD параллельна плоскости NНМ.А1ВDНМN
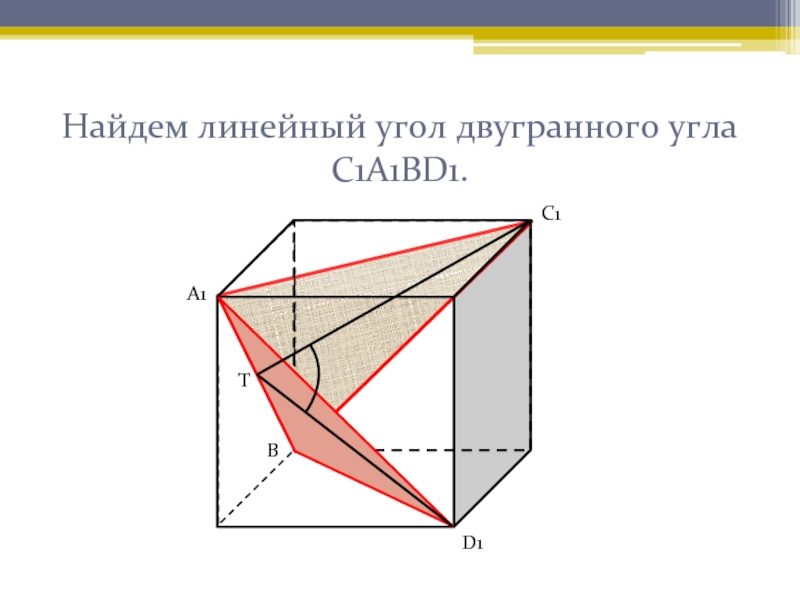
- 7. А1ВС1 пересекается с А1ВD1 по прямой А1В.А1С1ТD1В
- 8. Найдем линейный угол двугранного угла С1А1ВD1.А1С1ТD1В
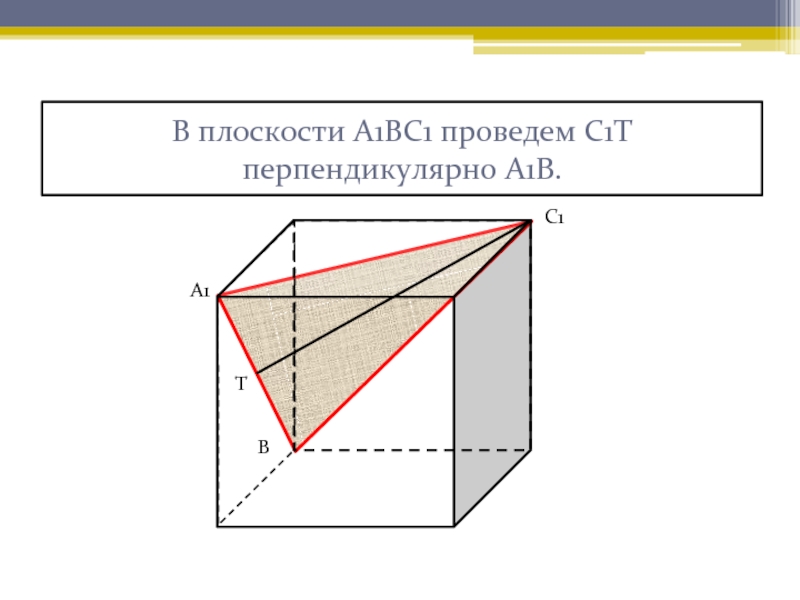
- 9. В плоскости А1ВС1 проведем С1Т перпендикулярно А1В.А1ВС1Т
- 10. В плоскости А1ВD проведем DТ перпендикулярно А1ВА1ВDТ
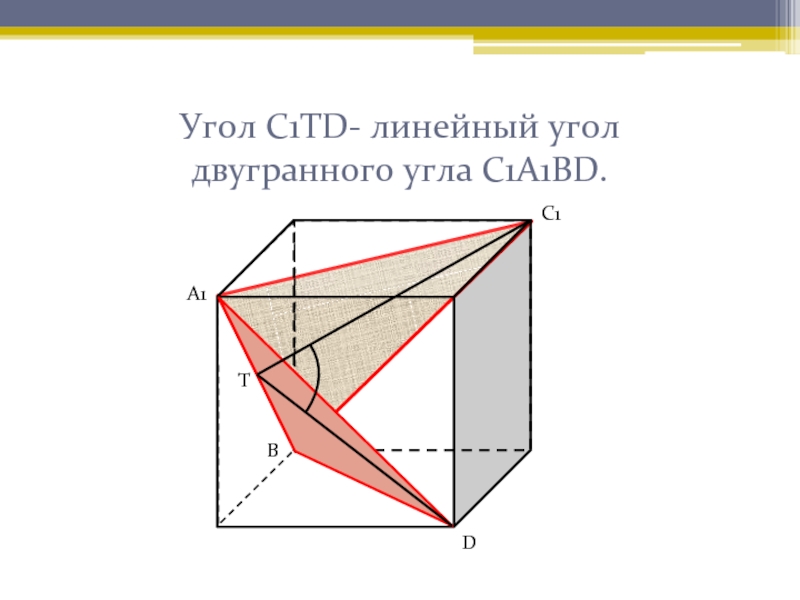
- 11. Угол С1ТD- линейный угол двугранного угла С1А1ВD.А1С1ТDВ
- 12. Найдем косинус угла С1ТD.А1С1ТDВ
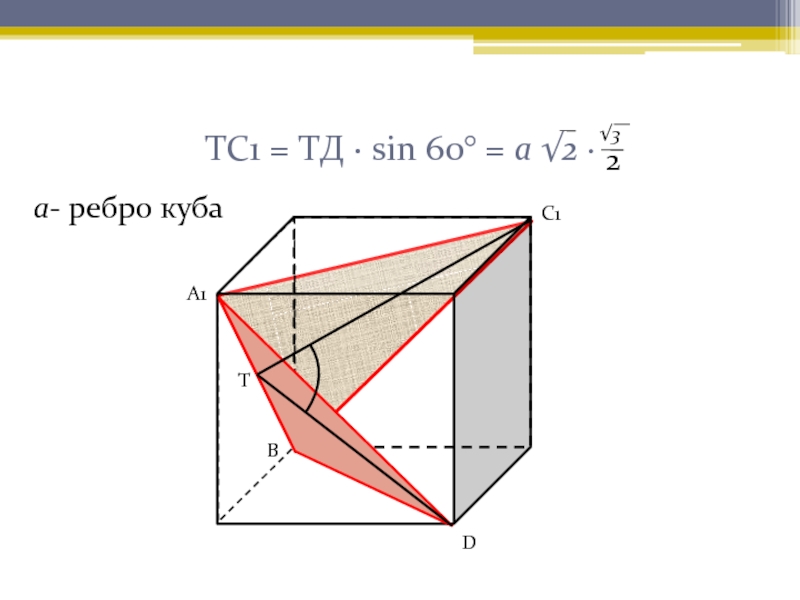
- 13. ТС1 = ТD1 = √3а- ребро кубаА1С1ТDВ2а
- 14. ТС1 = ТД · sin 60° = а √2 · А1С1ТDВ√32а- ребро куба
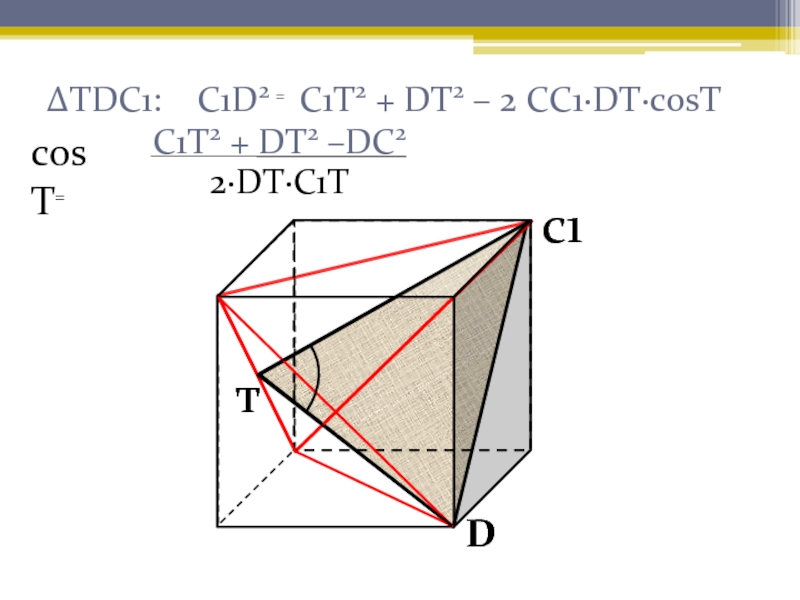
- 15. ΔTDC1: C1D2 ₌ C1T2 + DT2
- 16. Находим cos T:сosT₌₌₌Ответ:..
- 17. Спасибо за внимание.
- 18. Скачать презентанцию
Данная тема актуальна, так как подобные задачи требуют развитого абстрактного мышления. Задачи, представленные ниже, чаще всего вызывают затруднения при решении у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких
Слайды и текст этой презентации
Слайд 1
Угол между плоскостями
Решение задач уровня С.
Муниципальное общеобразовательное учреждение
средняя общеобразовательная
школа №85
Слайд 2
Данная тема актуальна, так как подобные задачи требуют развитого абстрактного
мышления. Задачи, представленные ниже, чаще всего вызывают затруднения при решении
у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких задач.Нахождение угла между скрещивающимися прямыми и угла между плоскостями
Слайд 3Аргументы
1. Определение куба.
2. Определение правильной призмы.
3. Свойства правильной призмы.
4. Свойство
средней линии треугольника.
5. Признак параллельности плоскостей.
6. Определение угла между плоскостями.
7.
Линейный угол двугранного угла.8. Теорема Пифагора.
9. Теорема косинусов.
Слайд 4Задача. В кубе найти косинус угла между плоскостями
КЕР и NМН, где К,
Е, Р, N, Н, М – середины ребер А1В1, В1С1, ВВ1, АА1, АВ, АD .А
А1
В1
С1
С
D
D1
В
К
Е
Р
N
М
H
Теги