Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок алгебры на тему "Квадратные уравнения"
Содержание
- 1. Урок алгебры на тему "Квадратные уравнения"
- 2. Цели:Закрепить определение квадратных уравнений, их виды.Отработать навыки решения квадратных уравнений.Развитие логики мышления;Развитие познавательного интереса.
- 3. «Стоимость билета» В поездку мы возьмём
- 4. Слайд 4
- 5. Остановка №1 станция «Повторение».Остановка первая. И это
- 6. Станция «Повторение». Алгоритм решения квадратного уравнения:ах²+вх+с=0Определить коэффициенты а,в,сЕсли D0, то1 кореньУравнение не имеет корней
- 7. Станция «Повторение».Объясните, в чём заключается смысл ограничения
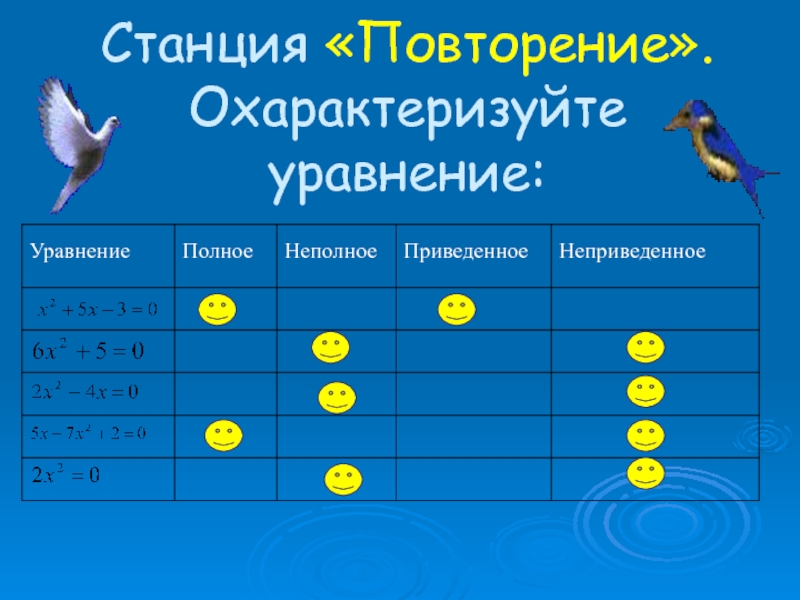
- 8. Станция «Повторение». Охарактеризуйте уравнение:
- 9. Ребята, скорее в путь!
- 10. Остановка №2 станция «Решение»Ну что же, повторенье
- 11. Станция «Решение»Ребята, вы в билет свой посмотрите:Увидите,
- 12. Если правильно Вы всё решили, Слово «ДОБРО»
- 13. По словарю В.И.Даля:ДОБРО – всё положительное, хорошее,
- 14. «Добрый человек – не тот, кто умеет
- 15. Ребята, скорее в путь!
- 16. РАЗМИНКА
- 17. Остановка №4 Станция «ИСТОРИЧЕСКАЯ» Необходимость решать
- 18. Станция «ИСТОРИЧЕСКАЯ» Правило решения этих уравнений,
- 19. Станция «ИСТОРИЧЕСКАЯ» «Кто хочет ограничиться настоящим
- 20. Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один
- 21. Ребята, скорее в путь!
- 22. Остановка №5 Станция «ЛЮБОЗНАТЕЛЬНАЯ».Стёпа Смекалкин, не решая
- 23. Станция «ЛЮБОЗНАТЕЛЬНАЯ».Если числа а и с одного
- 24. Ребята, скорее в путь!
- 25. Остановка №6 Станция «Размышлялки»После такого трудного путиОтдыха
- 26. Станция «Размышлялки»
- 27. Ребята, скорее в путь!
- 28. Остановка №7 «НАХОДКА»Задача Бхаскары.Обезянок резвых стаяВсласть поевши
- 29. Решение:
- 30. Остановка №8 Станция «ИТОГОВАЯ»Какие виды квадратных уравнений вы знаете?Каков алгоритм решения квадратного уравнения?
- 31. Домашнее задание. Оторвите по полоске часть билета – это ваше домашнее задание.
- 32. Успехов!!!До новых встреч!
- 33. Скачать презентанцию
Цели:Закрепить определение квадратных уравнений, их виды.Отработать навыки решения квадратных уравнений.Развитие логики мышления;Развитие познавательного интереса.
Слайды и текст этой презентации
Слайд 2Цели:
Закрепить определение квадратных уравнений, их виды.
Отработать навыки решения квадратных уравнений.
Развитие
логики мышления;
Слайд 3«Стоимость билета»
В поездку мы возьмём только тех, кто
вовремя «купит билеты» - правильно заполнит карточки с заданиями.
Слайд 5Остановка №1
станция «Повторение».
Остановка первая.
И это – Повторенье.
Гласит пословица, что
это – мать учения. Итак, давайте-ка мы вспомним, Что называется квадратным уравненьем?
Составьте алгоритм
решения квадратного уравнения.
Слайд 6Станция «Повторение».
Алгоритм решения квадратного уравнения:
ах²+вх+с=0
Определить
коэффициенты а,в,с
Если D
D=0, то
2 корня
Если D>0, то
1 корень
Уравнение не
имеет корней
Слайд 7Станция «Повторение».
Объясните, в чём заключается смысл ограничения в определении квадратного
уравнения а ≠ 0?
Перечислите виды квадратных уравнений.
Какое уравнение называется неполным
квадратным уравнением? Приведите пример.Какое уравнение называется приведённым квадратным уравнением? Приведите пример.
Сколько корней может иметь квадратное уравнение?
Слайд 10Остановка №2
станция «Решение»
Ну что же, повторенье
Для нас уж пройденный
этап,
И методы решенья уравнений
Пора на практике нам применять.
РЕШЕНИЕ –
вторая наша станция.Здесь главное – найти решенье,
Проявите всё своё уменье!
Слайд 11Станция
«Решение»
Ребята, вы в билет свой посмотрите:
Увидите, что уравнений - ровно
пять.
Задача ваша – в меру поспешите-
Ответы верные ко всем искать.
Найдя,
заносите вы в клетку букву,Которая стоит под верным решеньем.
И вот тогда прочтёте вы наверно,
Шифрованное слово – итог закономерный.
Слайд 12Если правильно Вы всё решили,
Слово «ДОБРО» Вы получили.
Даже по
буквам оно больше зла!
А уж по сути…Доброта ведь мир спасла!
У
других ребят ответы тоже правильные есть:Решили если правильно, то это слово – ЧЕСТЬ.
Честь была в любые времена
Самым главным достояньем человека.
ЧЕСТЬЮ НАДО ДОРОЖИТЬ ВСЕГДА!
И здесь ничто не может быть помехой!
Станция «Решение»
Слайд 13По словарю В.И.Даля:
ДОБРО – всё положительное, хорошее, полезное.
ЧЕСТЬ:
Достойные уважения и
гордости моральные качества и этические принципы личности;
Хорошая репутация и доброе
имя;Почёт и уважение.
Слайд 14«Добрый человек – не тот, кто умеет делать добро, а
тот, кто не умеет делать зла».
В.О.Ключевский
Доброму сухари в пользу, а злому и мясо не впрок. (рус. пословица)
Добру и злу дано всегда сражаться.
И в вечной битве зло сильнее тем,
Что средства для добра не все годятся,
Меж тем как зло не брезгует ничем.
Мирза Шафи
Слайд 17Остановка №4
Станция «ИСТОРИЧЕСКАЯ»
Необходимость решать уравнения не только первой,
но и второй степени ёщё в древности была вызвана потребностью
решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, как неполные, так и полные квадратные уравнения.Слайд 18Станция «ИСТОРИЧЕСКАЯ»
Правило решения этих уравнений, изложенное в вавилонских
текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне
до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.Слайд 19Станция «ИСТОРИЧЕСКАЯ»
«Кто хочет ограничиться настоящим без знания прошлого,
тот никогда его не поймет»
ЛейбницМатематики Древней Греции решали квадратные уравнения геометрически; например, Евклид – при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во
многих древних математических
рукописях и трактатах.
Слайд 20Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших
до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте
(около 598 г.).Среднеазиатский ученый ал-Хорезми (IX в.) в трактате «Китаб аль-джебр валь -мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической интерпретации.
Станция «ИСТОРИЧЕСКАЯ»
Слайд 22Остановка №5
Станция «ЛЮБОЗНАТЕЛЬНАЯ».
Стёпа Смекалкин, не решая уравнения вида
a x² +
с = 0
Сразу говорит, имеет оно корни или нет. А
вы сможете это сделать?Слайд 23Станция «ЛЮБОЗНАТЕЛЬНАЯ».
Если числа а и с одного знака, то уравнение
не имеет корней , если разных знаков, то имеет.
Приведите примеры
уравнений вида ах²+с=0Не имеющих корней
Имеющих корнями дробные числа
Слайд 25Остановка №6
Станция «Размышлялки»
После такого трудного пути
Отдыха нам лучше не найти,
Чем
думать, размышлять, считать,
И корни уравнения искать!
Слайд 28Остановка №7
«НАХОДКА»
Задача Бхаскары.
Обезянок резвых стая
Всласть поевши развлекалась.
Их в квадрате часть
восьмая
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько ж было
обезьянок, Ты скажи мне, в этой стае?