Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок по теме "Арифметическая и геометрическая прогрессия"
Содержание
- 1. Урок по теме "Арифметическая и геометрическая прогрессия"
- 2. 1.Повторить ….2.Решать …3.Осуществлять самооценку …
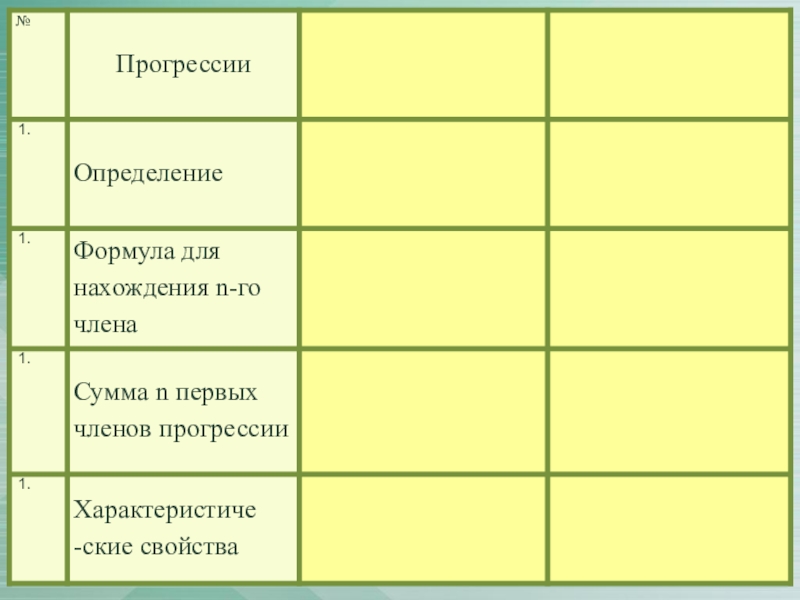
- 3. Арифметическая и геометрическая прогрессии
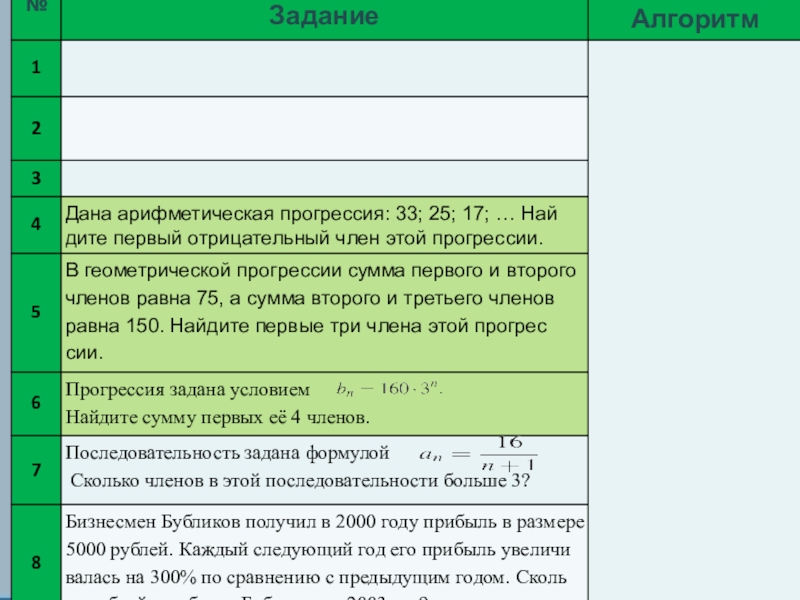
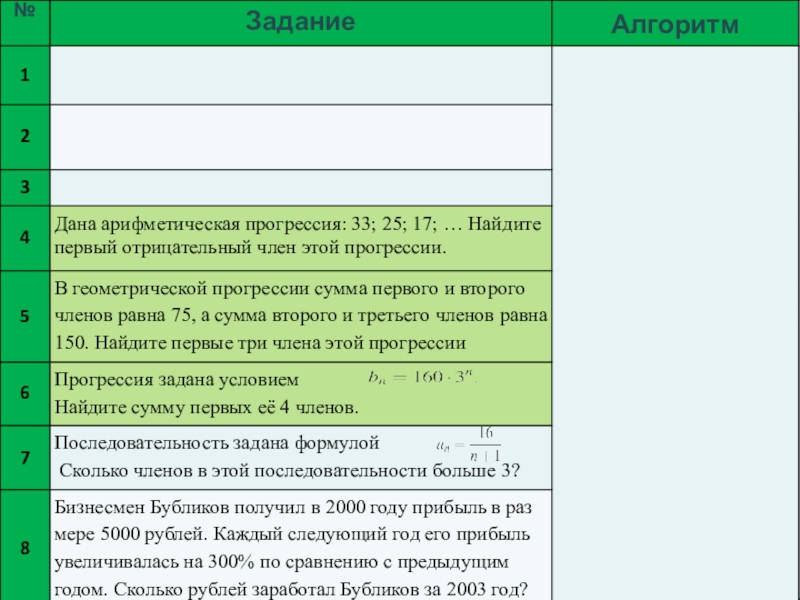
- 4. Цель:Закрепить навыки применения основных формул в
- 5. План урокаОргмомент, целеполагание Устная работаСамостоятельная работа с
- 6. Какая последовательность?1) 2; 5; 8; 11;14; 17;…
- 7. Слайд 7
- 8. Кто из ученых впервые употребил слово прогрессия ?Боэций
- 9. Слайд 9
- 10. В трактатах по дисциплинам квадривия — арифметике и музыке—
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Прогрессии в практических ситуациях В экономикеВ старинных задачах В природе В биологии
- 17. Задача – легендаИндийский царь Шерам вызвал к
- 18. Как думаете царь разгневался зря?
- 19. Это геометрическая прогрессия. Найдем ее сумму18 446 744 073 709 551 615
- 20. Быстрое размножение бактерий Бактерии размножаются делением одной
- 21. Задача про гриппРазберем простую задачку. Вася заболел
- 22. Подставим наши данные в формулу суммы геометрической прогрессии
- 23. Какая связь у задачи про грипп с
- 24. Слайд 24
- 25. Расти в геометрической прогрессии – это как
- 26. Закончи предложение:1. Арифметической прогрессией называется…2. Геометрической прогрессией
- 27. Слайд 27
- 28. Скачать презентанцию
1.Повторить ….2.Решать …3.Осуществлять самооценку …
Слайды и текст этой презентации
Слайд 4Цель:
Закрепить навыки применения основных формул в ходе решения задач,
связанных с арифметической и геометрической прогрессиями
Слайд 5План урока
Оргмомент, целеполагание
Устная работа
Самостоятельная работа с самопроверкой (тест) на
приз Боэция.
Экспресс-опрос
6. Подготовительный этап к дифференцированной работе: составление алгоритма.
7.
Работа по уровням8.Сообщения «Прогрессии в практических ситуациях»
9. Итог урока
Слайд 6Какая последовательность?
1) 2; 5; 8; 11;14; 17;…
2) 3; 9;
27; 81; 243;…
3) 1; 6; 11; 16; 21;…
4) –4;
–8; –16; –32; … 5) 5; 25; 125; 625;…
6) –2; –4; – 6; – 8; …
Слайд 10В трактатах по дисциплинам квадривия — арифметике и музыке— передал европейской цивилизации
метод и базовые знания лучших греческих авторов (преимущественно пифагорейцев) в области
«математических» наук. Возможно, также написал учебники геометрии и астрономии. Квадривиальные учебники — самые ранние работы Боэция; они традиционно датируются 500—506 гг.Боэций (крайний слева, подглядывающий в записи пишущего Пифагора) на Рафаэлевой фреске «Афинская школа»
Боэций
Слайд 17Задача – легенда
Индийский царь Шерам вызвал к себе Сету, который
придумал шахматы, для того, чтобы отблагодарить его за столь интересную
игру. Сета попросил у царя за первую шахматную клетку 1 зерно пшеницы, за вторую – 2 зерна, за третью - 4, таким образом, за каждую последующую клетку в 2 раза больше зерна. Царь разгневался, сказав, что просьба слуги не достойна царской щедрости, однако пообещал, что он получит свои зерна за все 64 клетки.Слайд 20Быстрое размножение бактерий
Бактерии размножаются делением одной клетки на две,
каждая из этих двух в свою очередь также делится на
две и получается 4 бактерии, потом 8 и т.д. Если одну бактерию поместить в идеальные условия с обилием пищи, то за одни сутки её потомство должно составить281 474 976 710 656 клеток. Таким образом, мы имеем дело с примером геометрической прогрессии в природе.
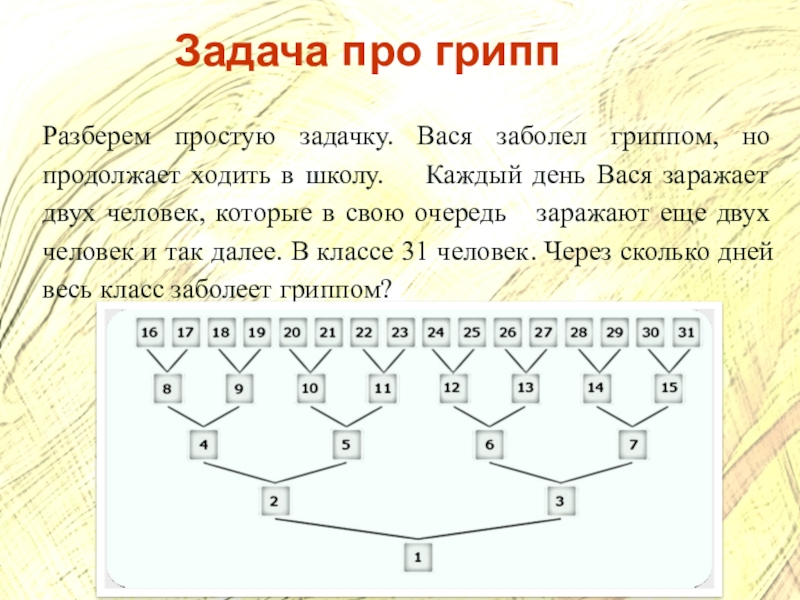
Слайд 21Задача про грипп
Разберем простую задачку. Вася заболел гриппом, но продолжает
ходить в школу. Каждый день Вася заражает двух человек,
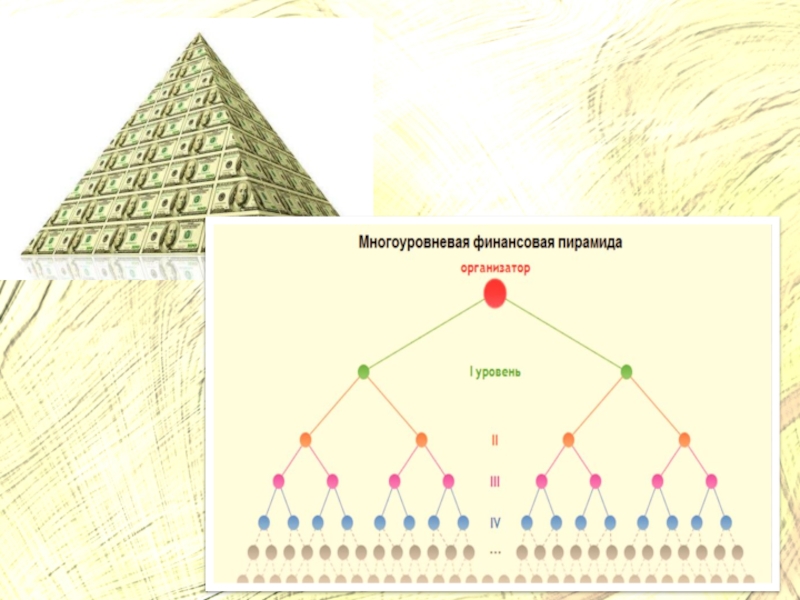
которые в свою очередь заражают еще двух человек и так далее. В классе 31 человек. Через сколько дней весь класс заболеет гриппом?Слайд 23Какая связь у задачи про грипп с задачей про финансовую
пирамиду
Как вы видите подобная, задача и рисунок к ней напоминает
пирамиду, в которой каждый последующий «приводит» новых людей. Однако рано или поздно настает такой момент, когда последние не могут никого привлечь. В нашем случае, если представить, что класс изолирован, 16 человек из 31 замыкают цепочку. Таким образом, если бы 31 человек были вовлечены в финансовую пирамиду, в которой деньги давались в случае, если приведешь двух других участников, то 16 человек не привели бы никого, соответственно, потеряли бы, что вложили в эту финансовую аферу.Слайд 25Расти в геометрической прогрессии – это как ?
Это выражение имеет
математический смысл, оно означает и бурный, неудержимый рост или
развитие чего-либо в повседневной жизни. Например в геометрической прогрессии может расти капитал, коллекция или собрание, количество мусора на улицах и прочее. В алгебре рост в геометрической прогрессии предусматривает умножение каждого нового члена прогрессии на одно и тоже число, в самом простом случае на 2. Поэтому не сложно представить, что будет происходить на наших улицах, если количество мусора действительно будет удваиваться ежедневно. А вот для развивающейся компании такой рост означает приятную прибыль и перспективу.Слайд 26Закончи предложение:
1. Арифметической прогрессией называется…
2. Геометрической прогрессией называется…
3. Если q
больше 1 ,то геометрическая прогрессия …
4.Если d меньше 0, то
арифметическая прогрессия…5. В математических моделях практических ситуаций используется быстрый рост …