Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уялинская средняя школа им.С.Садвакасова
Содержание
- 1. Уялинская средняя школа им.С.Садвакасова
- 2. Квадраттық функцияның y= ax2+n y= a(x-m)2 дербес
- 3. Теориялық материалды қайталау
- 4. 1.Қандай фукцияны квадраттық функция деп атайды?
- 5. у = ах2+bх+с түріндегі функцияныквадраттық функция деп
- 6. у=5х2-6 4) у=4х22) у=7х-1
- 7. 3. y=ax2y= ax2+ny= a(x-m)2функциялардағы а коэффициенті нені білдіреді?
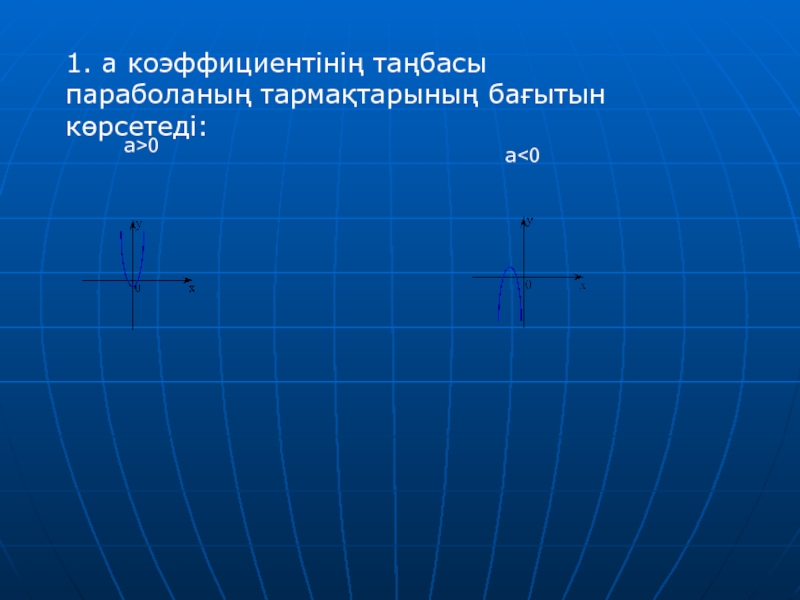
- 8. 1. а коэффициентінің таңбасы параболаның тармақтарының бағытын көрсетеді:а>0а
- 9. y= а х2, y=ах2+n, y= а(х-m)2 функциялардың
- 10. 4. y= ax2+n функциясының графигін қалай салуға болады ?
- 11. y= ax2+n функциясының графигі y=ax2 функциясының графигінордината осі бойымен n>0 болғанда, жоғары немесеn
- 12. 5. y= a(x-m)2 функциясының графигін қалай салуға болады?
- 13. y= a(x-m)2 функциясының графигі y=ax2 функциясының графигін абсцисса осі бойымен m>0 болғанда, оңға қарай немесе m
- 14. 6. y= a(x-m)2+n функциясының графигін қалай салуға болады ?
- 15. 1. y=ax2 функциясының графигінабсцисса осі бойымен m>0 болғанда, оңға қарай немесе m0 болғанда, жоғары немесеn
- 16. Ауызша есептер шығару
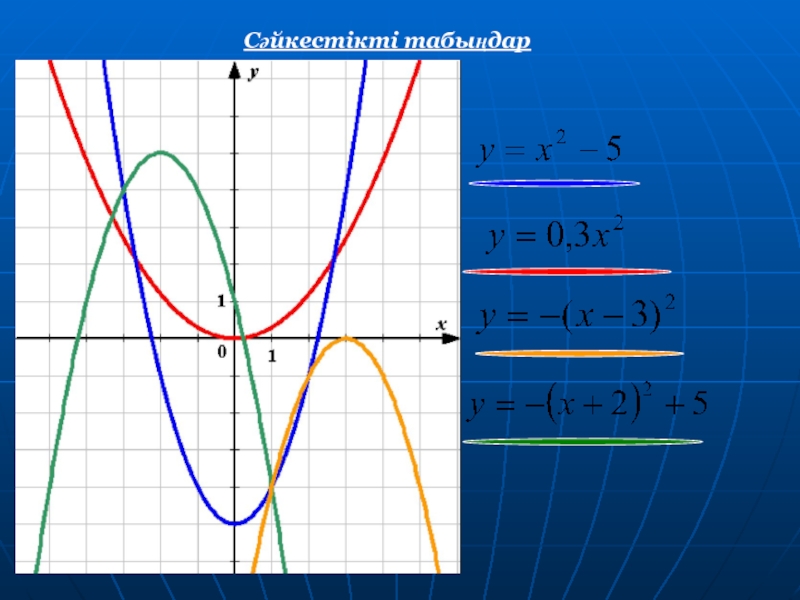
- 17. Сәйкестікті табыңдар
- 18. Квадраттық функция келесі формуламен берілген. Парабола
- 19. y= 0,5(x-1)2+4 функциясының графигін y=0,5x2 функциясының графигіненқалай
- 20. тапсырманы тексеру Шығармашылық
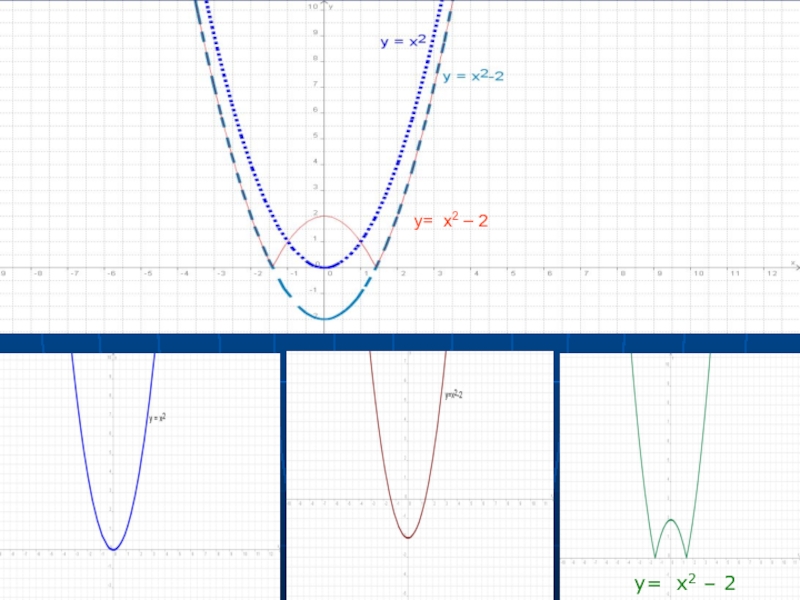
- 21. y= x2 – 2 функциясының
- 22. y= x2 – 2 y= x2 – 2
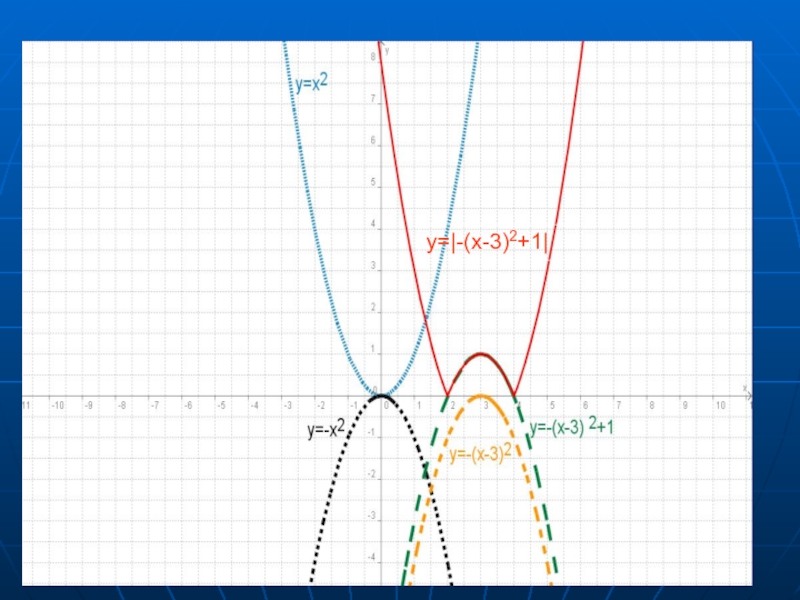
- 23. y=|-(x-3)2+1|
- 24. y=|-(x-3)2+1|
- 25. Практикалық жұмысy=x2 үлгісінің көмегімен :а) y=-x2-2
- 26. Т е с тБерілген көпмүшелердің қайсысы квадрат
- 27. Дұрыс жауаптар:1.Д 2.А
- 28. Үйге деңгейлік тапсырма:№ 253№257№262
- 29. Скачать презентанцию
Квадраттық функцияның y= ax2+n y= a(x-m)2 дербес түрлерін қайталау және белгілі графиктердің көмегімен квадраттық фунцияның графиктерінсалудағы оқушылардың білімдерін бекіту Сабақтың мақсаты:
Слайды и текст этой презентации
Слайд 2Квадраттық функцияның y= ax2+n
y= a(x-m)2 дербес түрлерін қайталау
және
белгілі графиктердің көмегімен
мақсаты:
Слайд 5у = ах2+bх+с түріндегі функцияны
квадраттық функция деп атайды
Мұндағы а, b,
c – нақты сандар, а≠0,
х – тәуелсіз айнымалы.
Слайд 6
у=5х2-6 4) у=4х2
2) у=7х-1
5) у=x3+x+1
3) у=-3х2+х+7 6) у=-9х2+4х
2.Берілген функциялардың қайсысы
квадраттық функция
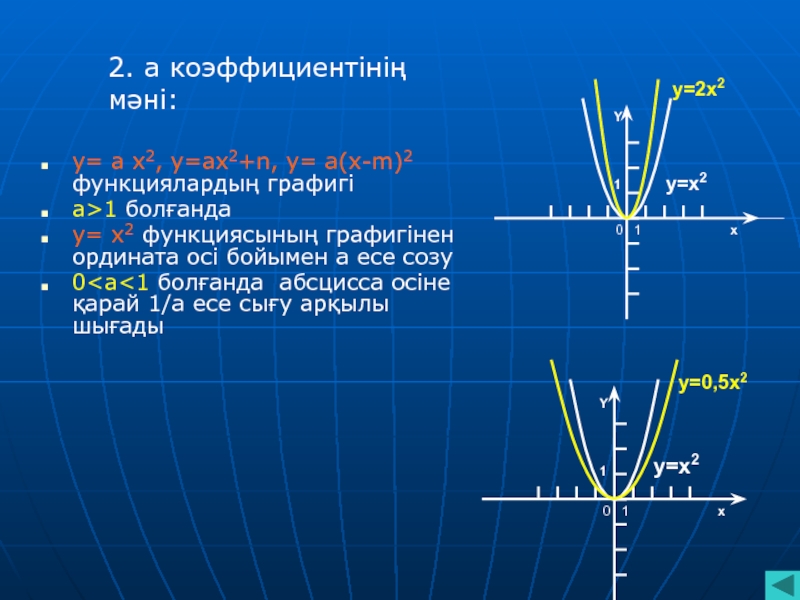
болады?
Слайд 9y= а х2, y=ах2+n, y= а(х-m)2 функциялардың графигі
а>1 болғанда
y= х2 функциясының графигінен ордината осі бойымен а есе созу
0<а<1 болғанда абсцисса осіне қарай 1/а есе сығу арқылы шығады
0 1 x
y=x2
y=2x2
0 1 x
y=x2
y=0,5x2
Y
1
Y
1
2. а коэффициентінің мәні:
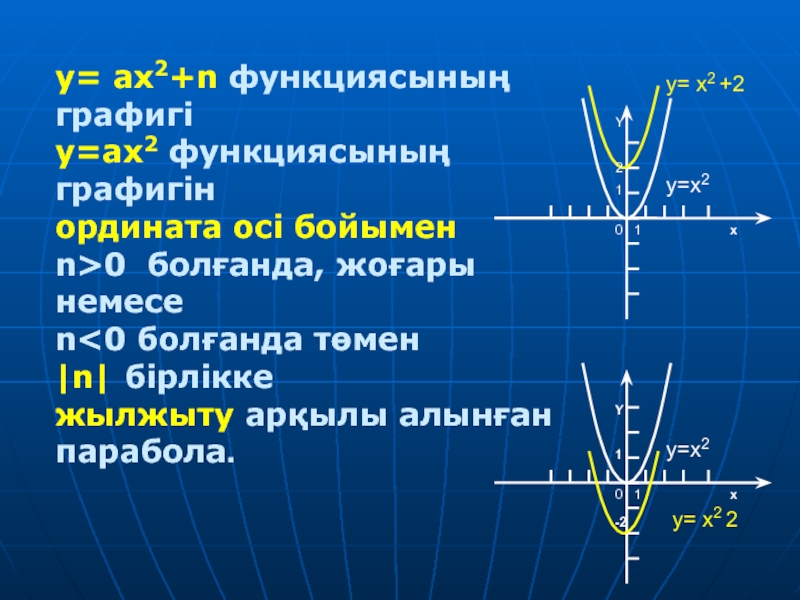
Слайд 11y= ax2+n функциясының графигі
y=ax2 функциясының графигін
ордината осі бойымен
n>0
болғанда, жоғары немесе
n
парабола.0 1 x
y= x2 +2
y=x2
0 1 x
y= x2 2
y=x2
Y
2
1
Y
1
-2
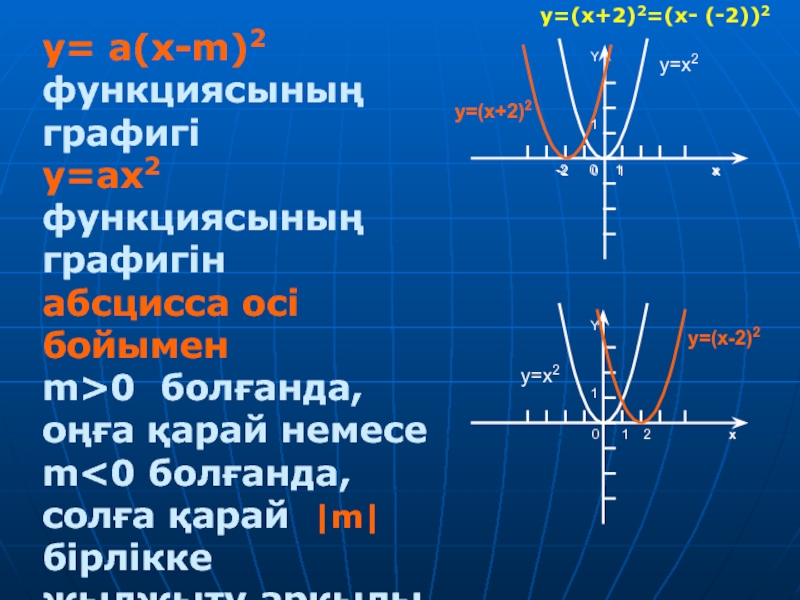
Слайд 13y= a(x-m)2 функциясының графигі
y=ax2 функциясының графигін
абсцисса осі бойымен
m>0 болғанда,
оңға қарай немесе m
бірлікке жылжыту арқылы алынған парабола.
-2 0 1 x
y=x2
y=(x+2)2
0 1 2 x
y=x2
y=(x-2)2
Y
1
Y
1
y=(x+2)2=(x- (-2))2
-2 0 1 x
Слайд 151. y=ax2 функциясының графигін
абсцисса осі бойымен
m>0 болғанда,
оңға қарай
немесе m
осі бойыменn>0 болғанда, жоғары немесе
n<0 болғанда төмен
|n| бірлікке
жылжытамыз.
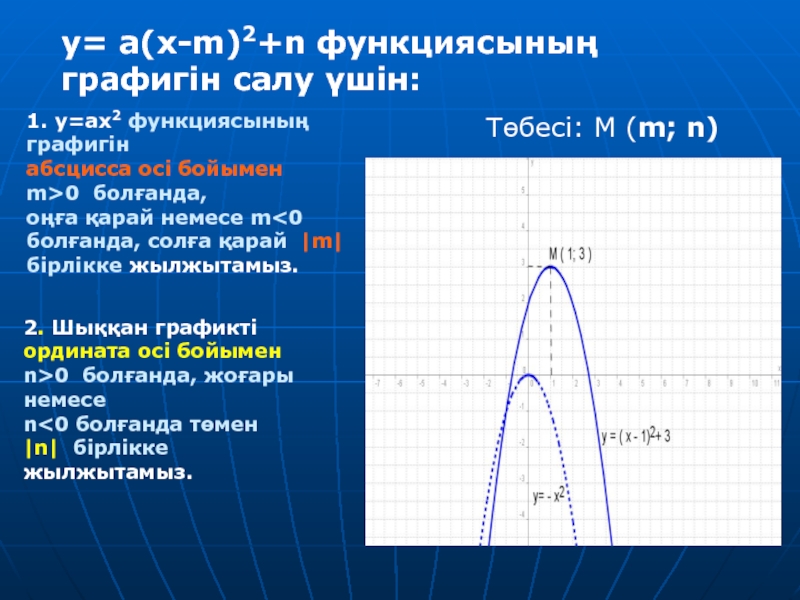
y= a(x-m)2+n функциясының
графигін салу үшін:
Төбесі: М (m; n)
Слайд 18 Квадраттық функция келесі формуламен берілген. Парабола төбесін анықтаңдар.
y =
x2 -6
y = (x-5)2
y = (x-7)2 +4
y =
(x+3)2 -1(0;-6)
(5;0)
(7;4)
(-3;-1)
Слайд 19y= 0,5(x-1)2+4 функциясының графигін
y=0,5x2 функциясының графигінен
қалай алуға болады?
Aбсцисса осі
бойымен 1бірлікке оңға жылжытамыз, өйткені m=1. Нәтижесінде 0,5(х-1)2 функциясының графигін
аламыз.Шыққан графикті ордината осі бойымен
4 бірлікке жоғары жылжытамыз,өйткені n=4
Шыққан парабола y= 0,5(x-1)2+4 функциясының графигі болады.
Слайд 25Практикалық жұмыс
y=x2 үлгісінің көмегімен :
а) y=-x2-2 ә) y=-(х+1)2
– 3
б) y=|-х2 +3| графиктерін салыңдар?
2. Салуды орындамай-ақ, функцияның
графигінің х осімен және у осіменен қиылысу нүктелерінің координаталарын табыңдар:а) y=х2+2х ә) y=х2 +2х-8
Слайд 26Т е с т
Берілген көпмүшелердің қайсысы квадрат үшмүше болады?
А) 2х+3
В) х3 – х -7 С) х2-19х Д)
3х2 -9х -12. х2 -9х+8 квадрат үшмүшесін көбейткіштерге жіктеңдер:
А)(х-1)(х-8) В) (х+1)(х –9) С) (х+1)(х+8) Д)жіктеуге болмайды.
3.Суретте y=x2-4 функцияның графигі қандай түске боялған? А) қызыл В) көк С) жасыл Д) басқа
4. y=(x+5)2 функцияның графигін y=x2 функцияның графигінен қалай алуға болады?
А) Ох осі бойымен 5 бірлік оңға В) Ох осі бойымен
5 бірлік солға С) Оу осі бойымен 5 бірлік төмен
Д) Оу осі бойымен 5 бірлік жоғары жылжыту арқылы алуға болады.
5. y=3x2+4х-7 параболаның х осімен қиылысу нүктелерінін абсциссаларын анықта:
А)1;-7/3 В) 1;7/3 С) 2;4 Д)8;1
