Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Виды симметрии. Урок по геометрии в 8 классе
Содержание
- 1. Виды симметрии. Урок по геометрии в 8 классе
- 2. Ее можно обнаружить почти везде, если знать,
- 3. Центральная ОсеваяЗеркальнаяCимметрия
- 4. Центральная симметрия Центральная симметрия – это
- 5. Фигура называется симметричной относительно точки О, если
- 6. Центральная симметрияточка О – центр симметрии
- 7. Алгоритм построения центрально-симметричной фигурыПостроить: треугольник А 1В1
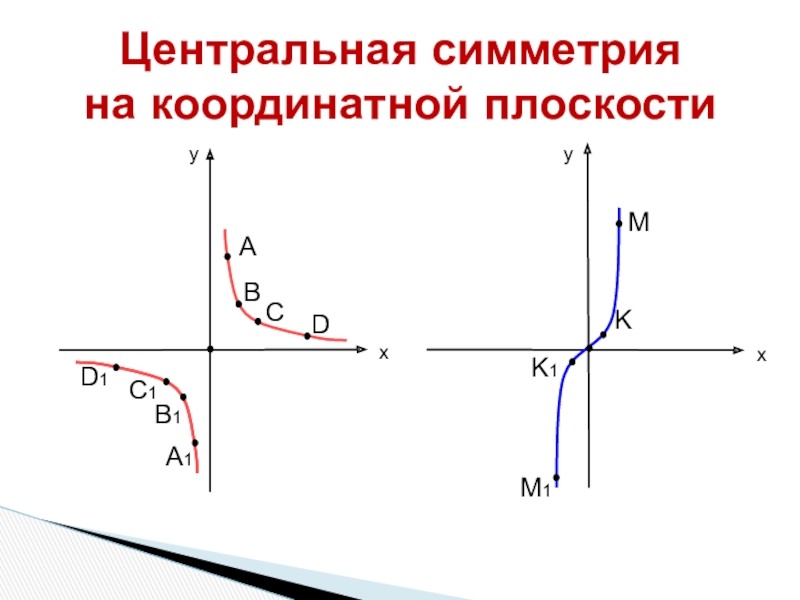
- 8. Центральная симметрия на координатной плоскостиyyxxABCDA1B1C1D1MKK1M1
- 9. Осевая симметрия Осевая симметрия – это
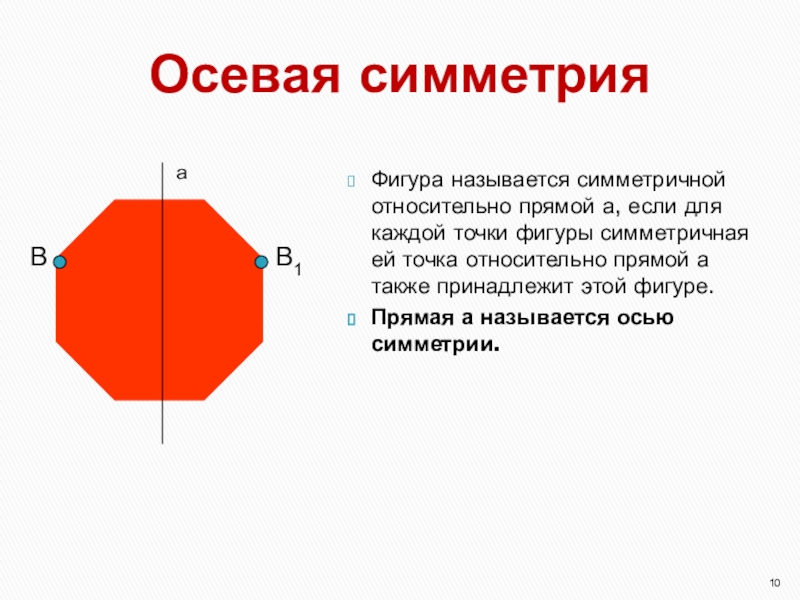
- 10. Осевая симметрияФигура называется симметричной относительно прямой а,
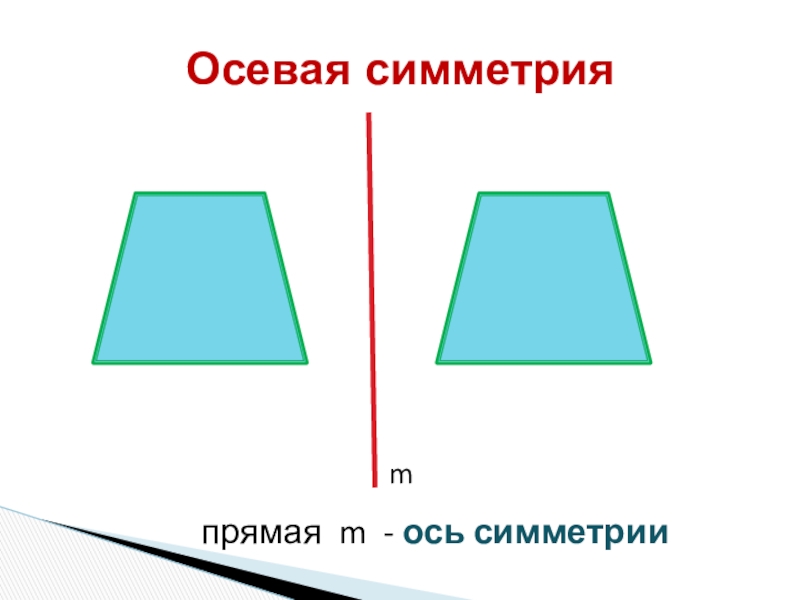
- 11. Осевая симметрияmпрямая m - ось симметрии
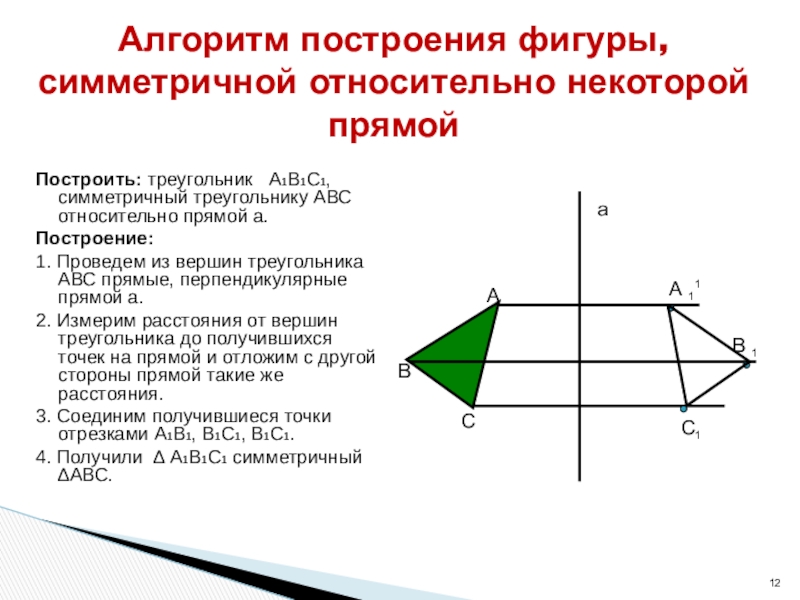
- 12. Алгоритм построения фигуры, симметричной относительно некоторой прямойПостроить:
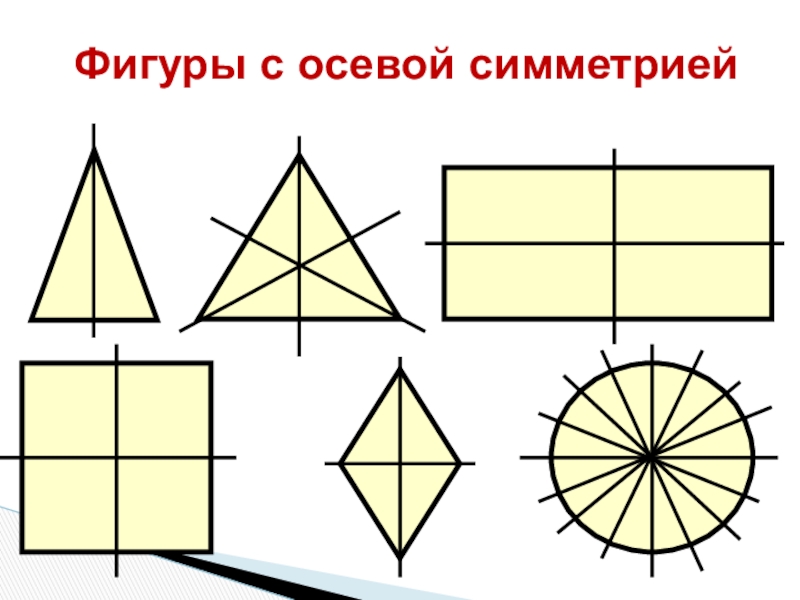
- 13. Фигуры с осевой симметрией
- 14. В Е Ж З К Н О
- 15. А Д Ж Л М Н О
- 16. Б Г И Р У Ц Ч Я ЩБуквы без оси симметрии
- 17. Зеркальная симметрия
- 18. осеваяосевая и центральная Виды симметрии
- 19. Осевая симметрия в растительном мире Характерная для деревьев симметрия конуса хорошо видна на примере дерева
- 20. Симметрия в растительном миреВеточки деревьев, кустарников и
- 21. Симметрия в животном миреОсевая симметрия хорошо видна у бабочек.
- 22. Симметрия в животном мире Можно сказать, что каждое
- 23. Симметрия в неживой природе Каждая снежинка
- 24. Симметрия в неживой природе Когда мы смотрим на
- 25. Симметрия в неживой природе Каждый камень является огромной
- 26. Симметрия в архитектурезеркальная
- 27. Симметрия в архитектуре
- 28. Симметрия в архитектуре
- 29. Здание МГУ им. М. В. ЛомоносоваЗдание Большого театра в МосквеСимметрия в архитектуре
- 30. Симметрия в архитектуре
- 31. Симметрия в живописи
- 32. Симметрия в химии проявляется в геометрической конфигурации
- 33. магнийжелезомедьСимметрия в химииМногие атомы располагаются в пространстве по принципу симметрии
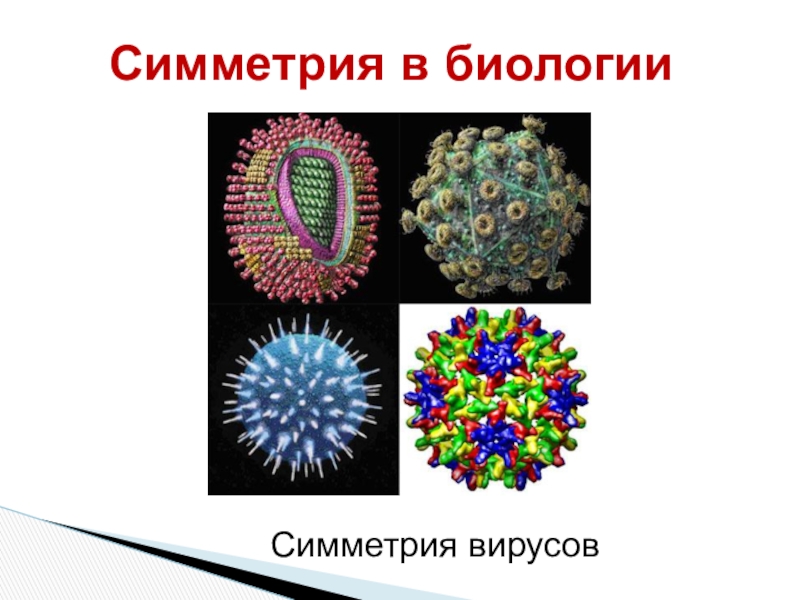
- 34. Симметрия вирусовСимметрия в биологии
- 35. Симметрия в быту
- 36. Характерной особенностью орнамента
- 37. Симметрия в технике
- 38. Симметрия в технике
- 39. Симметрия в технике
- 40. Тигр, о тигр, светло горящийВ глубине полночной
- 41. «Симметрия является той идеей, посредством которой человек
- 42. Список литературыАзевич А.И. Двадцать уроков гармонии: Гуманитарно-математический
- 43. Скачать презентанцию
Ее можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о ___________ в широком смысле – как об уравновешенности и гармонии. Творчество людей во
Слайды и текст этой презентации
Слайд 1**********
презентация к уроку геометрии
в 8 классе
Выполнила: учитель математики
Перелыгина
Е.А..
Слайд 2 Ее можно обнаружить почти везде, если знать, как ее искать.
Многие народы с древнейших времен владели представлением о ___________ в
широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к ________ Посредством __________ человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».ХХХХХХХХХ
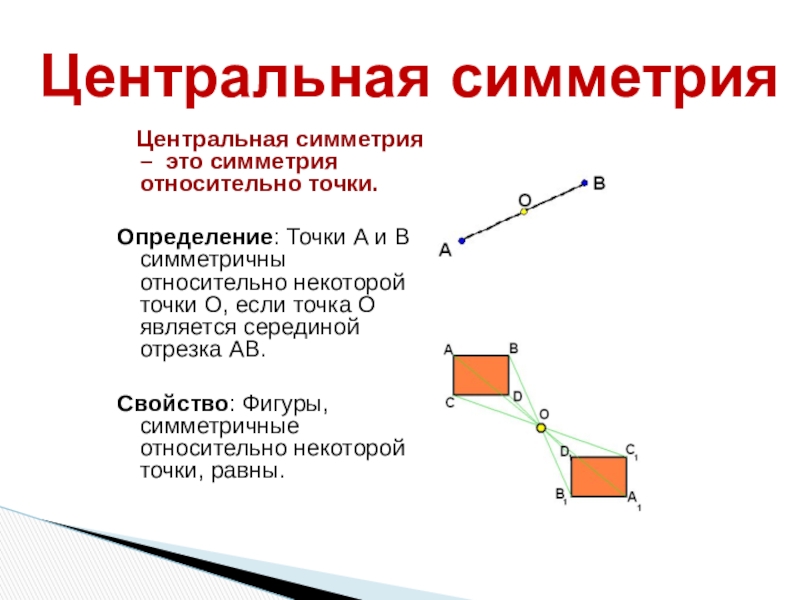
Слайд 4Центральная симметрия
Центральная симметрия – это симметрия
относительно точки.
Определение: Точки А и В симметричны относительно некоторой точки
О, если точка О является серединой отрезка АВ.Свойство: Фигуры, симметричные относительно некоторой точки, равны.
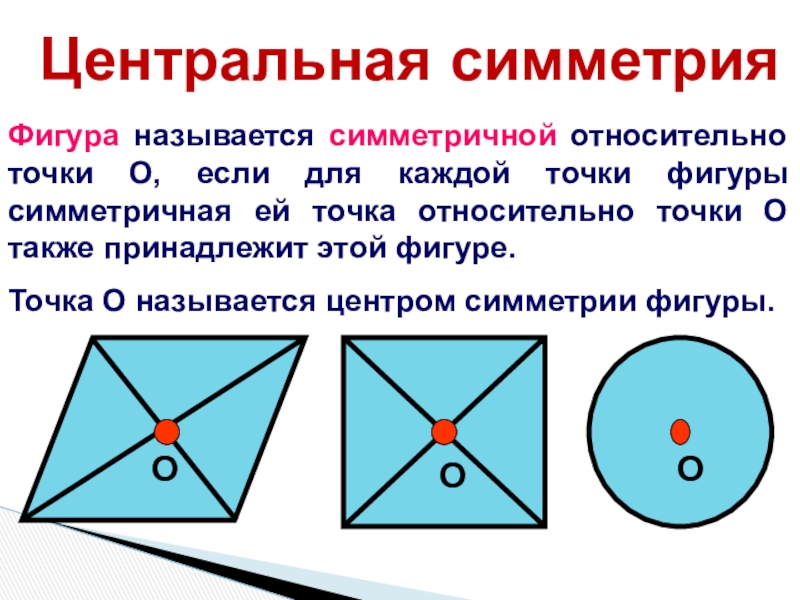
Слайд 5Фигура называется симметричной относительно точки О, если для каждой точки
фигуры симметричная ей точка относительно точки О также принадлежит этой
фигуре.Точка О называется центром симметрии фигуры.
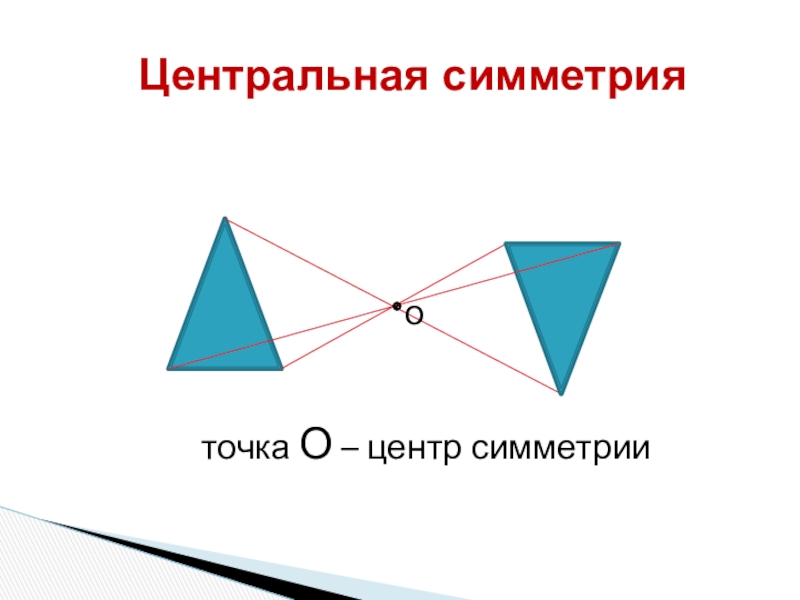
Центральная симметрия
О
О
О
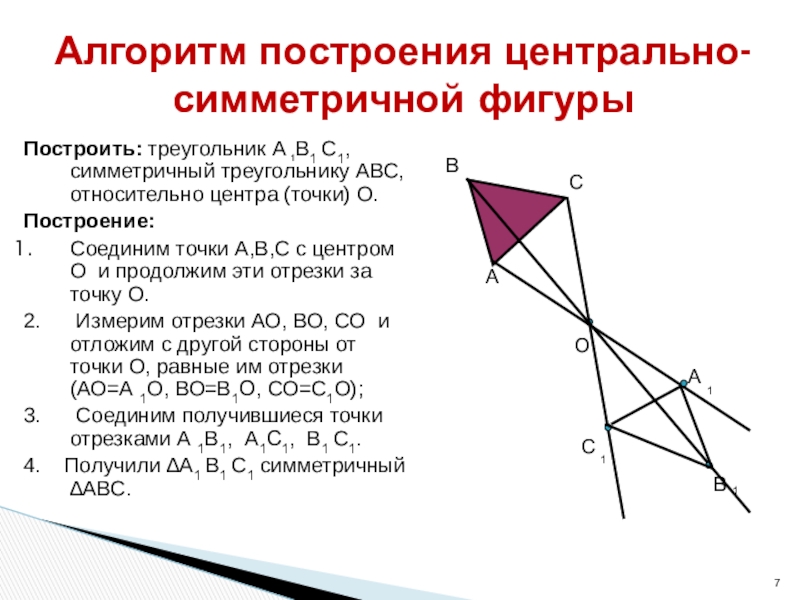
Слайд 7Алгоритм построения центрально-симметричной фигуры
Построить: треугольник А 1В1 С1, симметричный треугольнику
АВС, относительно центра (точки) О.
Построение:
Соединим точки А,В,С с центром
О и продолжим эти отрезки за точку О.2. Измерим отрезки АО, ВО, СО и отложим с другой стороны от точки О, равные им отрезки (АО=А 1О, ВО=В1О, СО=С1О);
3. Соединим получившиеся точки отрезками А 1В1, А1С1, В1 С1.
4. Получили ∆А1 В1 С1 симметричный ∆АВС.
А
В
С
О
С
1
А
В
1
1
Слайд 9Осевая симметрия
Осевая симметрия – это симметрия относительно проведенной
оси (прямой).
Определение: Точки А и В симметричны относительно некоторой прямой
а, если эта прямая проходит через середину отрезка АВ и перпендикулярна к нему.Прямая а называется осью симметрии.
Свойство: Две симметричные фигуры равны.
Рис. 1
Рис. 2
Слайд 10Осевая симметрия
Фигура называется симметричной относительно прямой а, если для каждой
точки фигуры симметричная ей точка относительно прямой а также принадлежит
этой фигуре.Прямая а называется осью симметрии.
а
В
В1
Слайд 12Алгоритм построения фигуры, симметричной относительно некоторой прямой
Построить: треугольник А1В1С1,
симметричный треугольнику АВС относительно прямой а.
Построение:
1. Проведем из вершин
треугольника АВС прямые, перпендикулярные прямой а.2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками А1В1, В1С1, В1С1.
4. Получили ∆ А1В1С1 симметричный ∆АВС.
А
В
С
С
А
В
1
1
1
1
а
Слайд 19Осевая симметрия
в растительном мире
Характерная для деревьев симметрия конуса хорошо
видна на примере дерева
Слайд 20Симметрия в растительном мире
Веточки деревьев, кустарников и растений сочетают в
себе зеркальную и переносную симметрию. Хорошо видна зеркальная и переносная
симметрия у веточек акации, папоротника .
Слайд 22Симметрия в животном мире
Можно сказать, что каждое животное, насекомое, рыба,
птица состоит из правой и левой половин . Симметричность формы
необходима рыбе, чтобы плыть, птице, чтобы летать, животному, чтобы бежать...
Слайд 23Симметрия в неживой природе
Каждая снежинка – это маленький кристалл
замерзшей воды. Форма снежинок может быть очень разнообразной, но все
они обладают симметрией – поворотной симметрией и зеркальной симметрией. У природных снежинок всегда шесть осей симметрии.
Слайд 24Симметрия в неживой природе
Когда мы смотрим на нагромождение камней у
подножия горы у нас может возникнуть мысль, что симметрия в
неорганическом мире – отнюдь не частый гость. Груда камней у подножия горы весьма беспорядочна.
Слайд 25Симметрия в неживой природе
Каждый камень является огромной колонией кристаллов, представляющих
собой в высшей степени симметричные «постройки» из атомов и молекул.
Слайд 31 Симметрия в живописи
Леонардо
да Винчи «Мадонна Литта»Фигуры мадонны и ребенка вписываются в правильный треугольник, который вследствие своей симметричности особенно ясно воспринимается глазом зрителя. Благодаря этому мать и ребенок сразу же оказываются в центре внимания, как бы выдвигаются на передний план. Голова мадонны совершенно точно, но в то же время естественно помещается между двумя симметричными окнами на заднем плане картины.
Слайд 32Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается
на специфике физических и химических свойств молекул в изолированном состоянии,
во внешнем поле и при взаимодействии с другими атомами и молекулами.Симметрия в химии
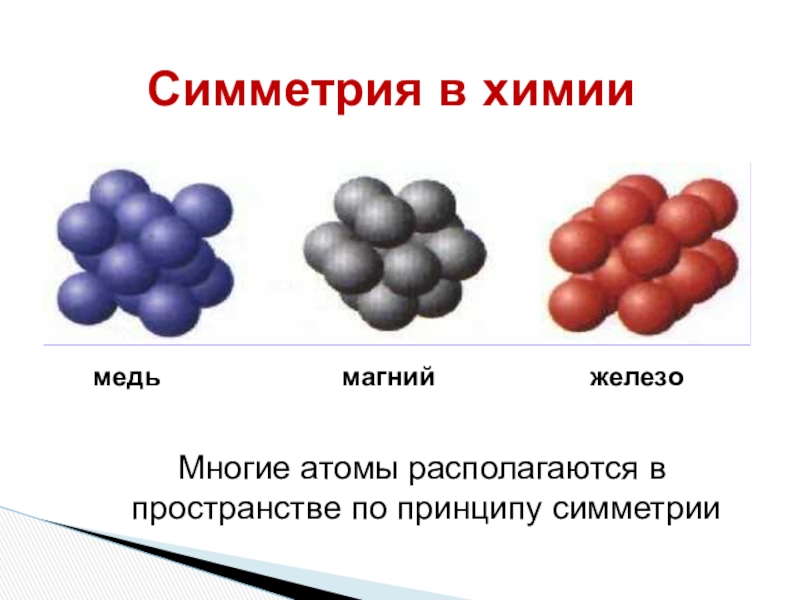
Слайд 33магний
железо
медь
Симметрия в химии
Многие атомы располагаются в
пространстве по принципу симметрии
Слайд 36
Характерной особенностью орнамента является симметричность отдельных
элементов рисунка, а часто и симметричность рисунка в целом.
Орнаменты
Орнамент (от лат. ornamentum — украшение), узор, состоящий из ритмически упорядоченных элементов
Слайд 40Тигр, о тигр, светло горящий
В глубине полночной чащи,
Кем задуман огневой
Симметричный
образ твой?
В поэзии симметрия проявляется в чередовании слогов, т.е. в
ритмичности
Симметрия в поэзии
Слайд 41«Симметрия является той идеей, посредством которой человек на протяжении веков
пытается постичь и создать порядок, красоту и совершенство»
Герман Вейль«
Слайд 42Список литературы
Азевич А.И. Двадцать уроков гармонии: Гуманитарно-математический курс. – М.:
Школа – Пресс, 1998.
Зенкевич И.Г. Эстетика урока математики. – М.:
Просвещение, 1981.Геометрия: Красота и гармония. Авт.-сост. Л.С. Сагателова, В.Н. Студенецкая. – Волгоград: Учитель, 2007.
Геометрия: Доп. Главы к шк. Учеб. 8 кл. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев. М.: Просвещение, 1996.
Семёнов С.Е. Изучаем геометрию: Кн. Для учащихся 6 – 8 классов сред. шк. – М.: Просвещение, 1987.
Тарасов Л.В. Этот удивительно симметричный мир: Пособие для учащихся. – М.: Просвещение, 1982.
Н. Д. Угринович Информатика. Базовый курс: Учебник для 8 класса / Н.Д. Угринович – М.: БИНОМ. Лаборатория знаний, 2005. - 205 с.: ил
Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. 5 – 6 кл.: Пособие для общеобразовательных учебных заведений. – М.: Дрофа,1999.
