Введение в мир фракталов

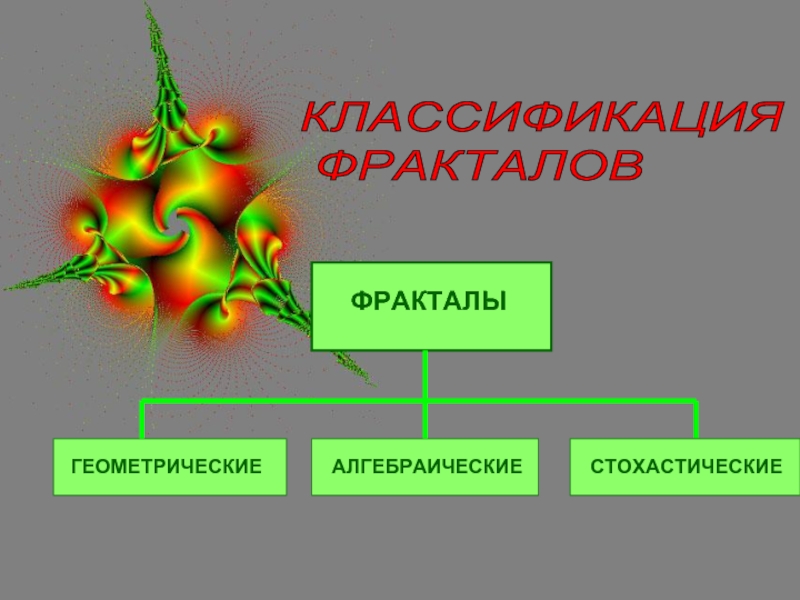
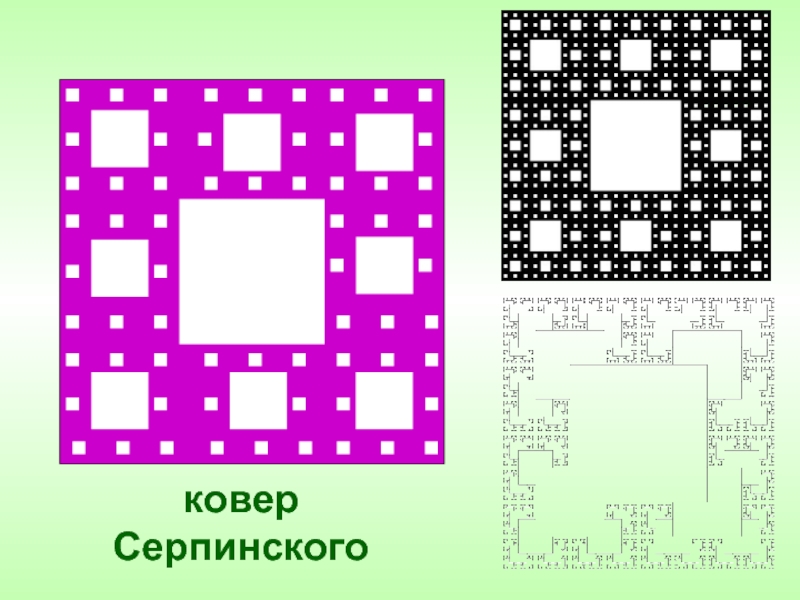
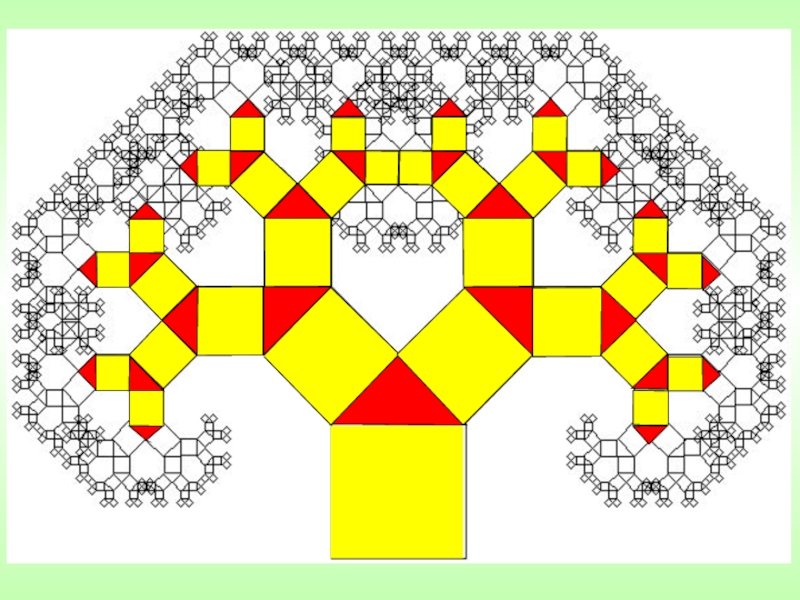
исследовательских работ «Интеллектуальное будущее Мордовии»
Секция: математика
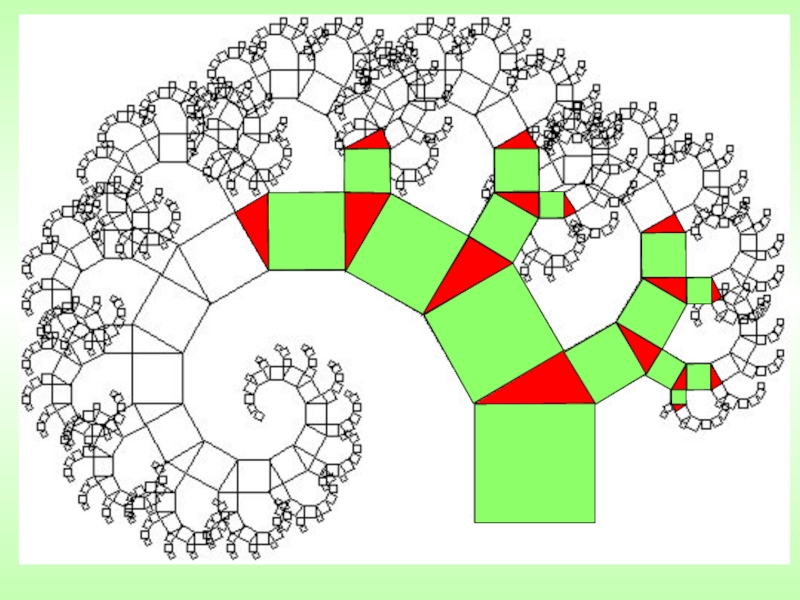
ВВЕДЕНИЕ В МИР ФРАКТАЛОВ
Автор

работы: ЯМАШКИН ПАВЕЛ,

Научный руководитель: Чудаева Е. В.,
учитель математики

математическим обоснованием графической интерпретации фрактальных образов
МЕТОДЫ ИЗУЧЕНИЯ
Анализ литературы по

теме исследования,
Изучение фракталов различного вида,
Разработать классификацию фракталов,
Собрать коллекцию фрактальных образов.

в природе

быть поделены на части, каждая из которых будет представлять уменьшенную

копию целого.
Fractal от латинского слова fractus, означает разбитый (поделенный на части).
Основное свойство фракталов: самоподобие, в самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.

ПОНЯТИЕ ФРАКТАЛА

в каждой точке.

Геометрические фракталы являются также самыми наглядными, т.к.

сразу видна самоподобность.

Для построения геометрических фракталов характерно задание «основы» и «фрагмента», повторяющегося при каждом уменьшении масштаба.

ГЕОМЕТРИЧЕСКИЕ ФРАКТАЛЫ

Серпинского

с помощью нелинейных процессов в n–мерных пространствах.

Самыми известными из них

являются множества Мандельброта и Жюлиа, Бассейны Ньютона

АЛГЕБРАИЧЕСКИЕ ФРАКТАЛЫ

функции

может быть сделано, пока точка z не выйдет за пределы

круга радиуса r 


Здесь z — комплексное число, соответствующее точке .

Множество Жюлиа — это множество таких точек, что отображения вида

не отображают их в окрестность бесконечности. На рисунке эти точки окрашены лиловым цветом.
Картинка получена выбором параметров a = 1.8, и b = 0.2 i и поворотом на 900

же процедуры, что и выше. Различие состоит в том, что

начальное значение для точки z берётся всегда равным нулю, а точке с координатами (х; у) на картинке соответствует комплексный параметр b = x + y i.

числа n, то получим многочисленный класс фрактальных множеств высокой симметрии,

порядок которой определяется натуральной степенью. Для составления программы Fractal5, которая вычисляет каждую итерацию по формуле f(z)=zn+c, где с=a+ib, пришлось использовать тригонометрическую форму задания комплексного числа

Фракталы множеств комплексных степеней.

п = 9

случайным образом изменяются какие-либо параметры.

Эти фракталы используются при моделировании рельефов

местности и поверхности морей, процесса электролиза.

Стохастические фракталы очень похожи на природные объекты – несимметричные деревья, изрезанные береговые линии.

СТОХАСТИЧЕСКИЕ ФРАКТАЛЫ

изучены различные виды фракталов.
3. Представлена классификация фракталов.
4. Собрана коллекция фрактальных

образов для первичного ознакомления с миром фракталов.
5. Составлены программы для построения графического образа фракталов.

ЗАКЛЮЧЕНИЕ