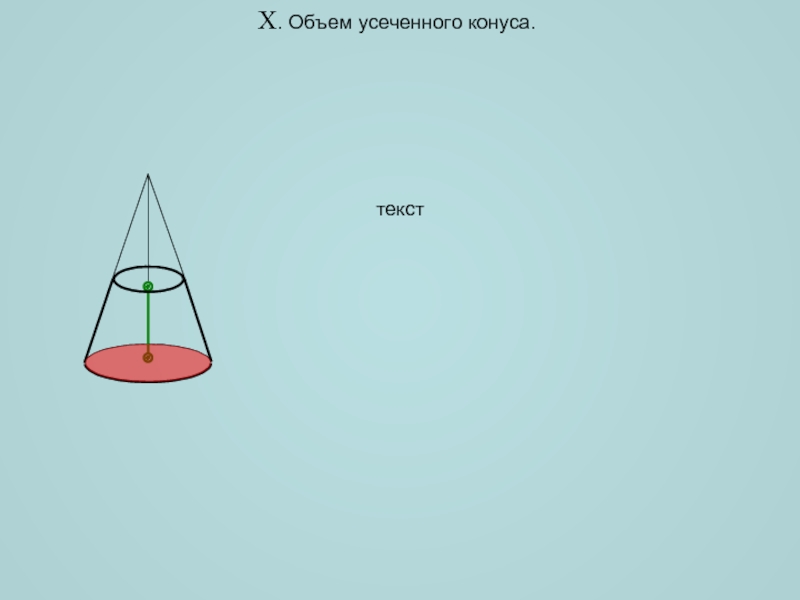
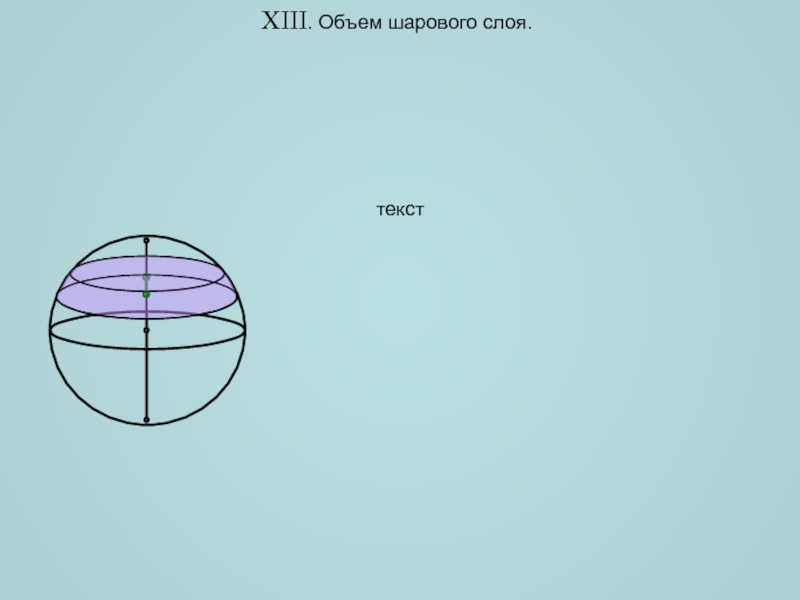
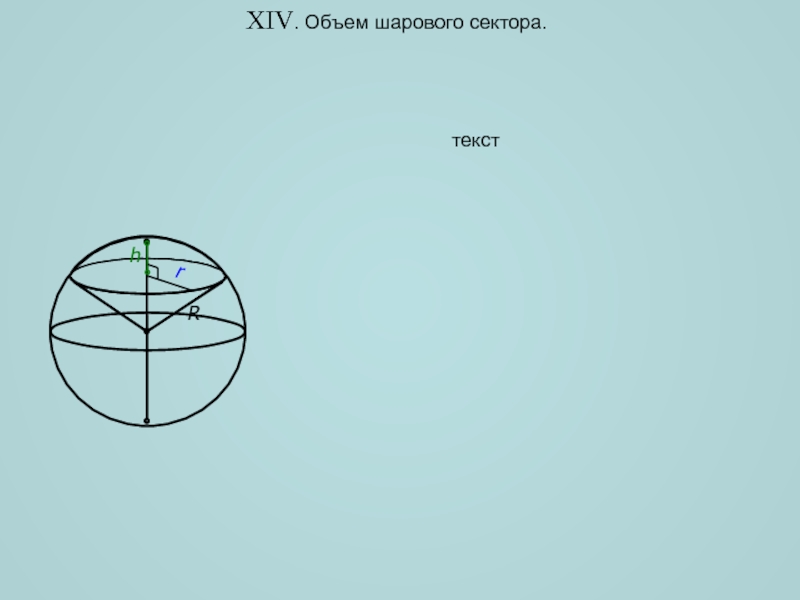
пространственных фигур, попробуем найти объем лимона. Ни на одно из
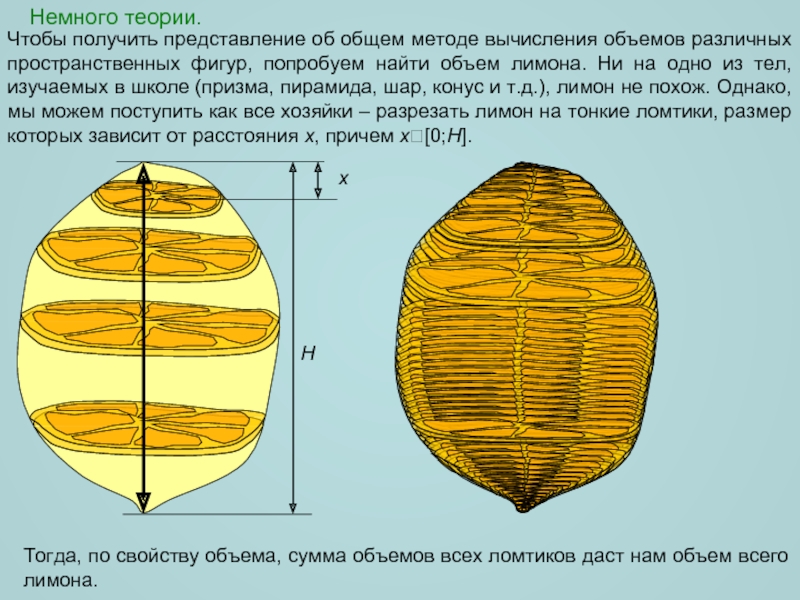
тел, изучаемых в школе (призма, пирамида, шар, конус и т.д.), лимон не похож. Однако, мы можем поступить как все хозяйки – разрезать лимон на тонкие ломтики, размер которых зависит от расстояния x, причем x[0;H].H
x
Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.



![Вычисление объемов пространственных тел с помощью интеграла I. Объем прямоугольного параллелепипедас высотой H и площадью основания S.xHx[0;H]0Площадь сечения I. Объем прямоугольного параллелепипедас высотой H и площадью основания S.xHx[0;H]0Площадь сечения не изменяется в любой точке отрезка](/img/thumbs/e88a450624f9ded1eb089bdd45464afe-800x.jpg)
![Вычисление объемов пространственных тел с помощью интеграла II. Объем прямой призмыс высотой H и площадью основания S.xx[0;H]H0Площадь сечения II. Объем прямой призмыс высотой H и площадью основания S.xx[0;H]H0Площадь сечения не изменяется в любой точке отрезка](/img/thumbs/deb3df9d62d9c683b0e9b9f6f6c9c48a-800x.jpg)
![Вычисление объемов пространственных тел с помощью интеграла III. Объем n-угольной прямой призмы с высотой H и площадью основания III. Объем n-угольной прямой призмы с высотой H и площадью основания S.xx[0;H]H0Площадь сечения не изменяется в любой](/img/tmb/1/79184/d8335a96d2c87da7f5aa157be5c6952a-800x.jpg)
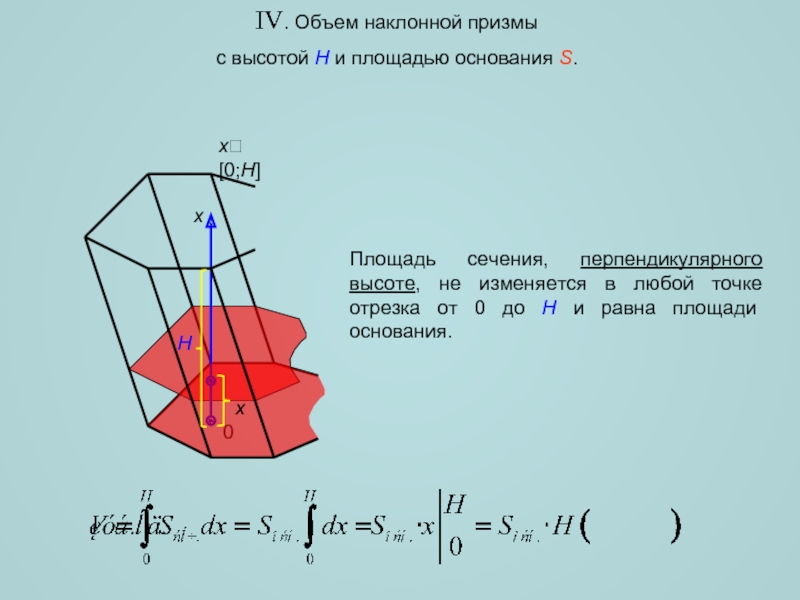
![Вычисление объемов пространственных тел с помощью интеграла V. Объем треугольной пирамидыс высотой H и площадью основания S.Hxx[0;H]⇒xПлощадь сечения V. Объем треугольной пирамидыс высотой H и площадью основания S.Hxx[0;H]⇒xПлощадь сечения изменяется в зависимости от расстояния x,](/img/thumbs/1d69f90b7c267580f89479966532f7bf-800x.jpg)
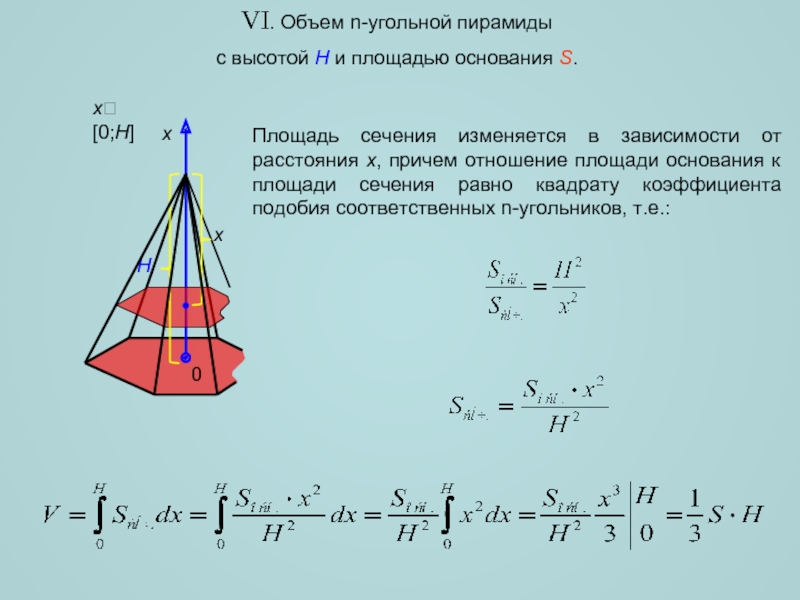

![Вычисление объемов пространственных тел с помощью интеграла VIII. Объем цилиндра с высотой H и площадью основания S.xx[0;H]H0xПлощадь сечения VIII. Объем цилиндра с высотой H и площадью основания S.xx[0;H]H0xПлощадь сечения не изменяется в любой точке отрезка](/img/thumbs/2384b6f24a53bf022a5ef34be52bb26d-800x.jpg)
![Вычисление объемов пространственных тел с помощью интеграла IX. Объем конуса с высотой H и площадью основания S.xx[0;H]HxПлощадь сечения IX. Объем конуса с высотой H и площадью основания S.xx[0;H]HxПлощадь сечения изменяется в зависимости от расстояния x,](/img/thumbs/46ac6b6481ecf96f08e76055eab97913-800x.jpg)