Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление площадей плоских фигур с помощью определенного интеграла
Содержание
- 1. Вычисление площадей плоских фигур с помощью определенного интеграла
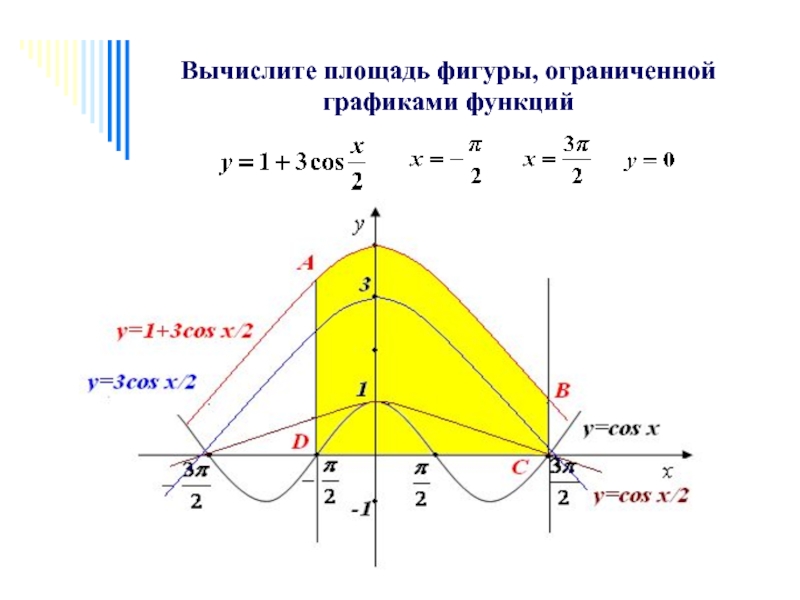
- 2. Вычислите площадь фигуры, ограниченной графиками функций
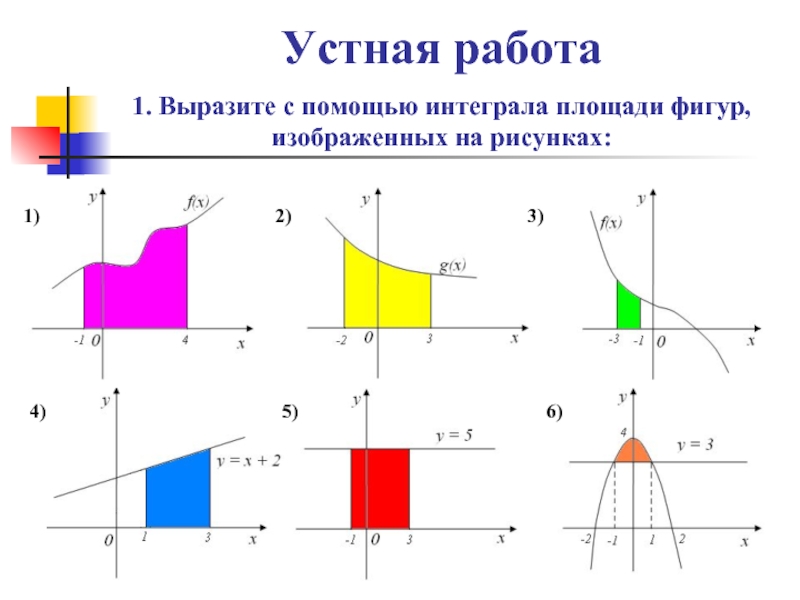
- 3. Устная работа 1. Выразите с помощью интеграла площади фигур, изображенных на рисунках:1)2)3)4)5)6)
- 4. 2. Вычислите интегралы:1).2).3).4).10,51641
- 5. Немного истории«Интеграл» придумал Якоб Бернулли (1690г.)«восстанавливать» от
- 6. Интеграл в древностиЭтот метод был подхвачен и
- 7. Исаак Ньютон (1643-1727) Наиболее полное изложение дифференциального
- 8. Лейбниц Готфрид Вильгельм (1646-1716) впервые использован Лейбницем
- 9. Определенный интегралИ. НьютонГ. Лейбницгде Формула Ньютона - Лейбница
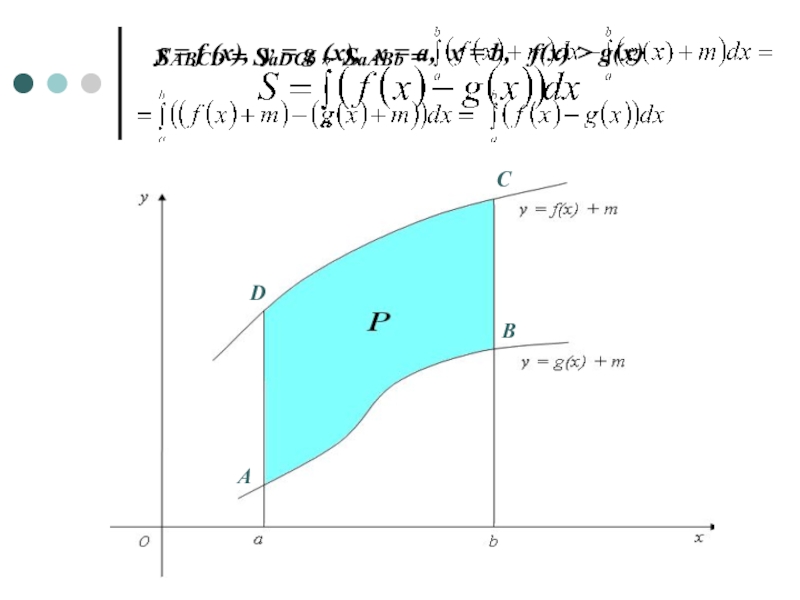
- 10. y = f (x), y = g
- 11. Пример. Вычислите площадь фигуры,
- 12. Задание1. Вычислите площадь фигуры,
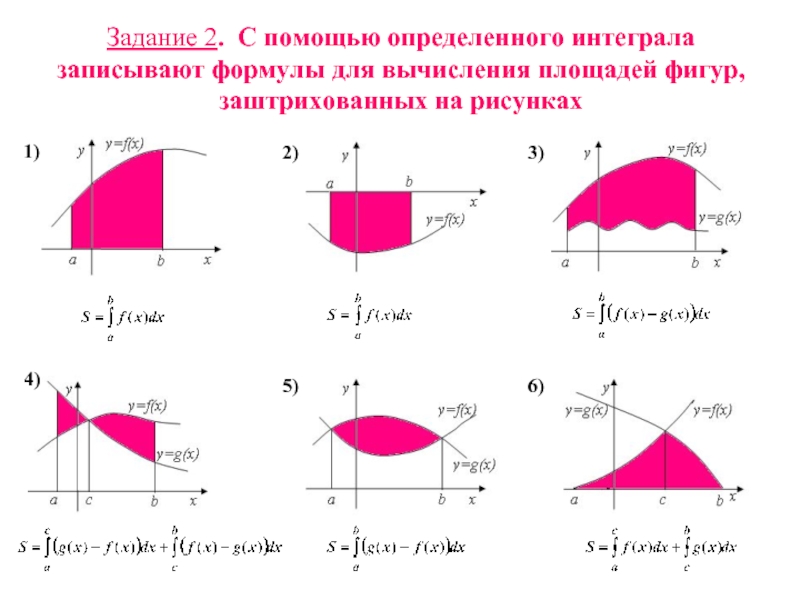
- 13. Задание 2. С помощью определенного интеграла записывают формулы для вычисления площадей фигур, заштрихованных на рисунках1)2)3)4)5)6)
- 14. Подберите из данных формул для вычисления площади
- 15. Задание 3. Вычислите площадь фигуры,
- 16. Итоги урока
- 17. СПАСИБО ЗА УРОК!Домашнее задание:1. п.4 стр.228 -
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема урока:
«Вычисление площадей плоских фигур с помощью определенного интеграла»
Учитель математики
Гурова
Ольга Валериевна
Слайд 3Устная работа 1. Выразите с помощью интеграла площади фигур, изображенных на
рисунках:
1)
2)
3)
4)
5)
6)
Слайд 5Немного истории
«Интеграл» придумал Якоб Бернулли (1690г.)
«восстанавливать» от латинского integro
«целый» от
латинского integer
от латинского
primitivus – начальный,
ввел
Жозеф Луи Лагранж
(1797г.)
«Примитивная функция»,
Слайд 6Интеграл в древности
Этот метод был подхвачен и развит Архимедом, и
использовался для расчёта площадей парабол и приближенного расчёта площади круга.
Евдокс Книдский
Архимед
Первым известным методом для расчёта интегралов является метод исчерпания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известен.
Слайд 7Исаак Ньютон
(1643-1727)
Наиболее полное изложение дифференциального и интегрального исчислений содержится в
«Методе флюксий...»
(1670–1671, опубликовано в 1736).
Переменные величины - флюенты(первообразная
или неопределенный интеграл)Скорость изменения флюент – флюксии (производная)
Слайд 8Лейбниц Готфрид Вильгельм
(1646-1716)
впервые использован Лейбницем в конце
XVII века
Символ
образовался из буквы
S — сокращения слова
summa (сумма)
Слайд 11Пример. Вычислите площадь фигуры,
ограниченной линиями
y = x, y = 5 – x, x = 1, x = 2.x
y
0
1
2
5
5
y = x
y = 5 - x
A
B
C
D
Слайд 12Задание1. Вычислите площадь фигуры,
ограниченной линиями
y = 3 –
x2,y = 1+ | x |
y = 1 + |x|
y
х
0
1
1
-1
3
y = 3 – х2
S1
S2
S = S1 + S2
Слайд 13Задание 2. С помощью определенного интеграла записывают формулы для вычисления
площадей фигур, заштрихованных на рисунках
1)
2)
3)
4)
5)
6)
Слайд 14Подберите из данных формул для вычисления площади фигуры ту, которая
подходит к одному из шести чертежей.
S1 =
S2 =
S3 =
S4
=S5 =
S6 =
5
1
2
3
4
6
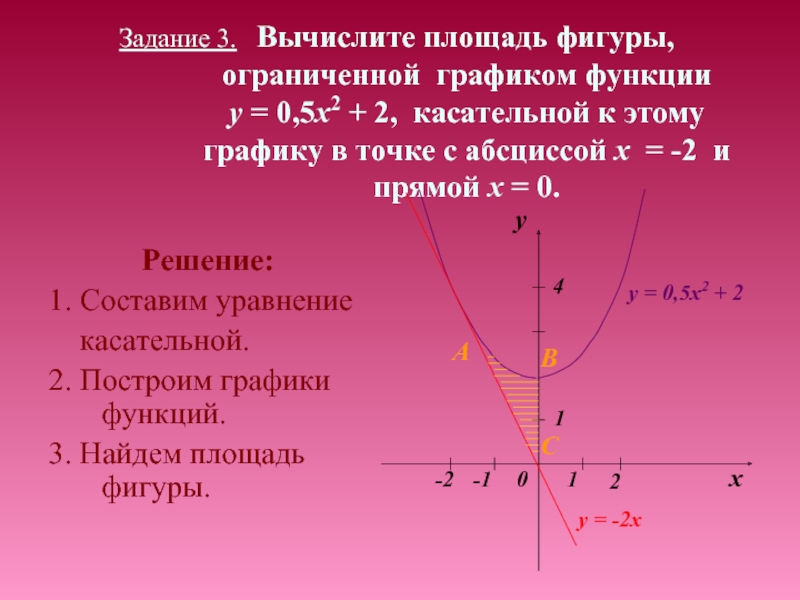
Слайд 15Задание 3. Вычислите площадь фигуры,
ограниченной графиком функции
y = 0,5x2 + 2, касательной к этому графику в точке с абсциссой х = -2 и прямой х = 0.Решение:
1. Составим уравнение
касательной.
2. Построим графики функций.
3. Найдем площадь фигуры.
х
y
0
-1
1
-2
1
4
у = -2х
у = 0,5х2 + 2
А
B
C
2