Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклые многоугольники
Содержание
- 1. Выпуклые многоугольники
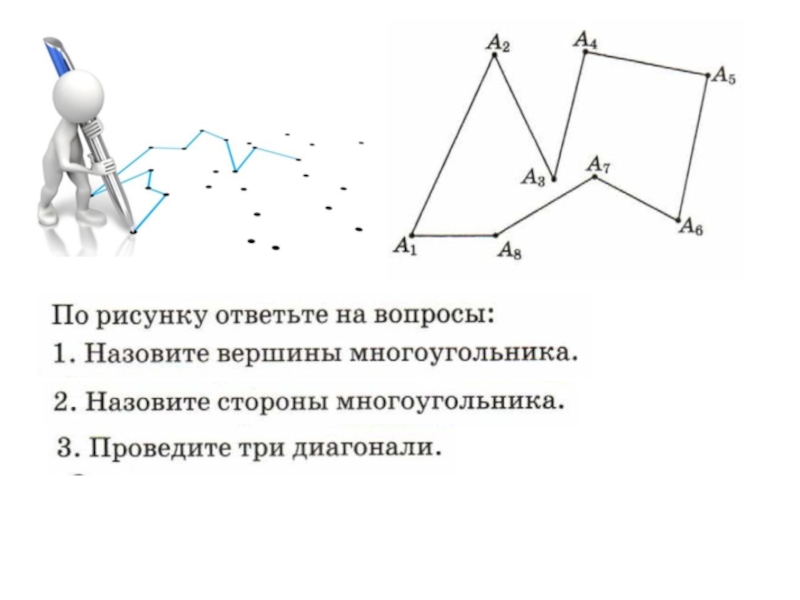
- 2. Что такое ломаная?Что такое замкнутая ломаная?Что значит простая ломаная?
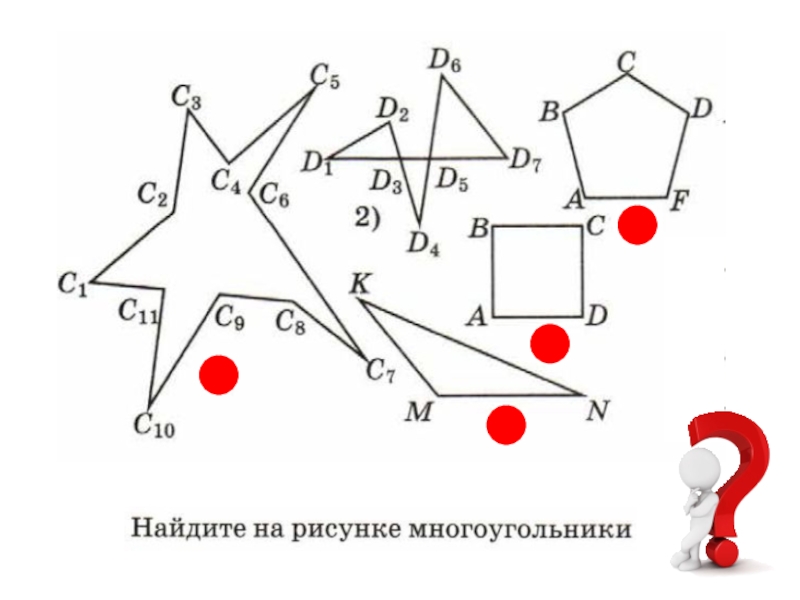
- 3. МНОГОУГОЛЬНИК – простая замкнутая ломаная, соседние звенья которой не лежат на одной прямой.
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. ПЛОСКИЙ МНОГОУГОЛЬНИК (многоугольная область) – конечная часть плоскости, ограниченная многоугольником.
- 8. ВЫПУКЛЫЙ МНОГОУГОЛЬНИК – многоугольник, который лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
- 9. Приведите примеры известных четырехугольников, которые являются выпуклыми многоугольниками.
- 10. Слайд 10
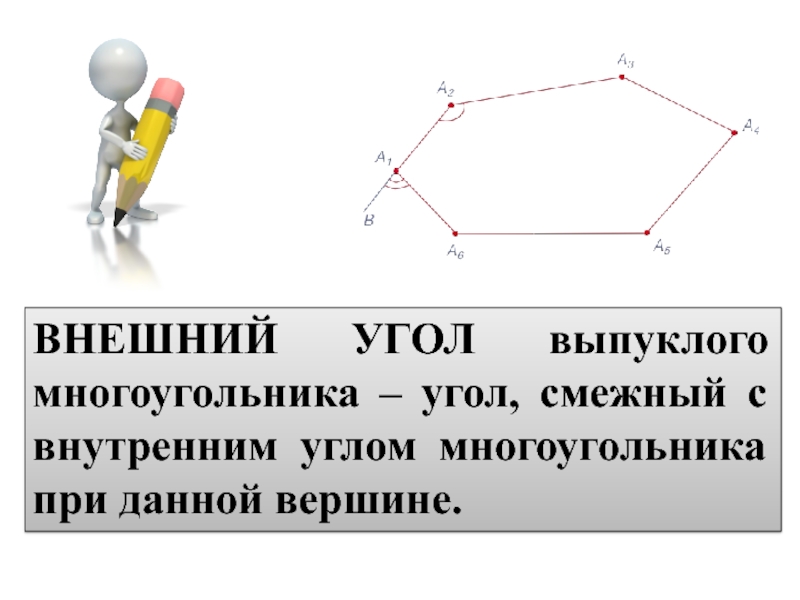
- 11. ВНЕШНИЙ УГОЛ выпуклого многоугольника – угол, смежный с внутренним углом многоугольника при данной вершине.
- 12. Теорема:Сумма углов выпуклого n-угольника равна 180°·(n – 2).Вычислите сумму углов выпуклогоа) пятиугольника;б) девятиугольника?
- 13. Сколько сторон имеет n-угольник, если сумма его внутренних углов равна: а) 1260°;б) 1980°?
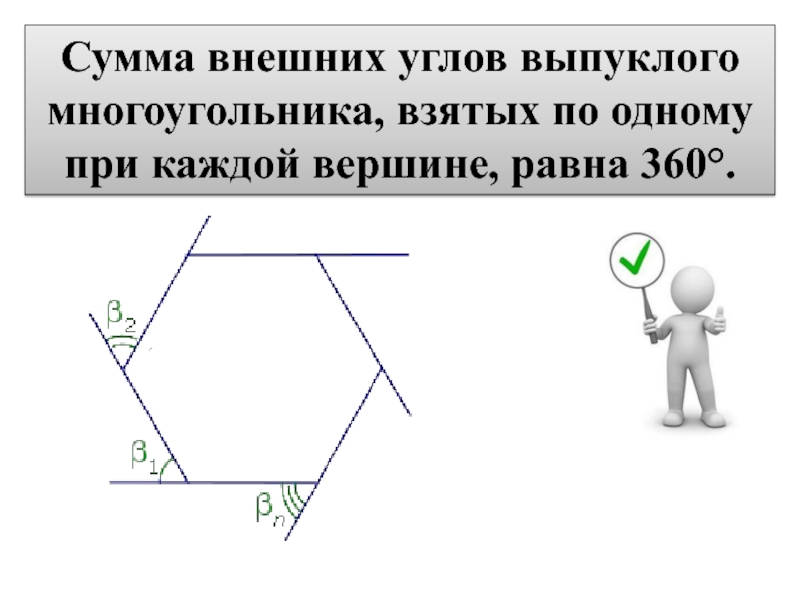
- 14. Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360°.
- 15. Сумма углов выпуклого многоуголь-ника в два раза
- 16. Сколько сторон имеет выпуклый многоугольник, если все
- 17. ДОМАШНЕЕ ЗАДАНИЕп. 115 №10Повторить п.38-41
- 18. Скачать презентанцию
Что такое ломаная?Что такое замкнутая ломаная?Что значит простая ломаная?
Слайды и текст этой презентации
Слайд 7ПЛОСКИЙ МНОГОУГОЛЬНИК (многоугольная область) – конечная часть плоскости, ограниченная многоугольником.
Слайд 8ВЫПУКЛЫЙ МНОГОУГОЛЬНИК – многоугольник, который лежит в одной полуплоскости относительно
любой прямой, содержащей его сторону.
Слайд 11ВНЕШНИЙ УГОЛ выпуклого многоугольника – угол, смежный с внутренним углом
многоугольника при данной вершине.
Слайд 12Теорема:
Сумма углов выпуклого
n-угольника равна 180°·(n – 2).
Вычислите сумму углов
выпуклого
а) пятиугольника;
б) девятиугольника?
Слайд 14Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой
вершине, равна 360°.
Слайд 15Сумма углов выпуклого многоуголь-ника в два раза меньше суммы внешних
углов, взятых по одному при каждой вершине. Найдите число сторон
этого многоугольника.
Слайд 16Сколько сторон имеет выпуклый многоугольник, если все его внешние углы
тупые?
Сколько сторон имеет выпуклый многоугольник, если сумма его внутренних углов
с одним из внешних равна 2250°?
