Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимно обратные функции
Содержание
- 1. Взаимно обратные функции
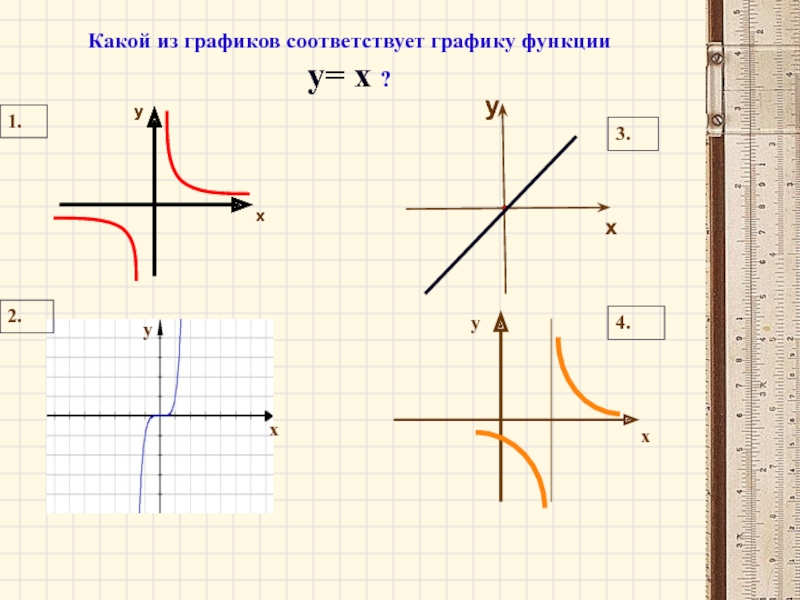
- 2. Какой из графиков соответствует графику функции у= х ?хуху1.2.3.4.
- 3. Какой
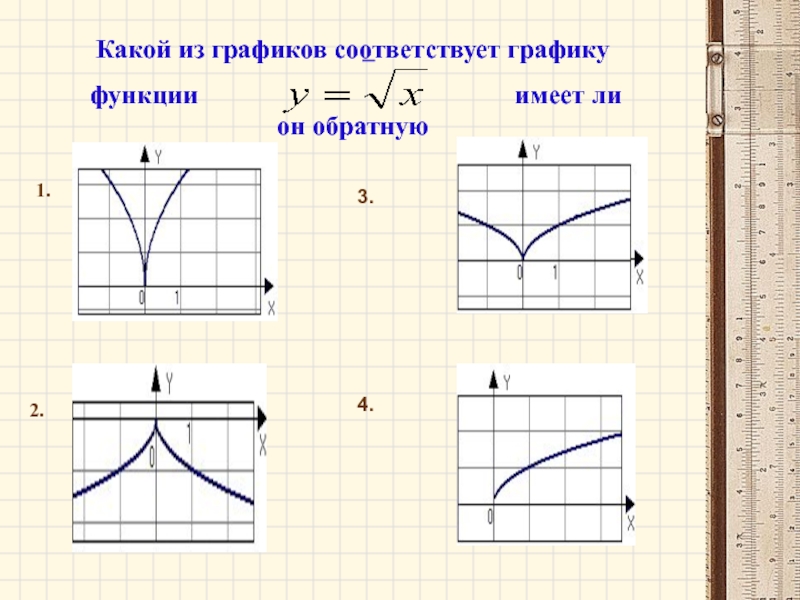
- 4. Какой из графиков соответствует графику функции имеет ли он обратную ?1.2.3.4.
- 5. Какой из графиков соответствует
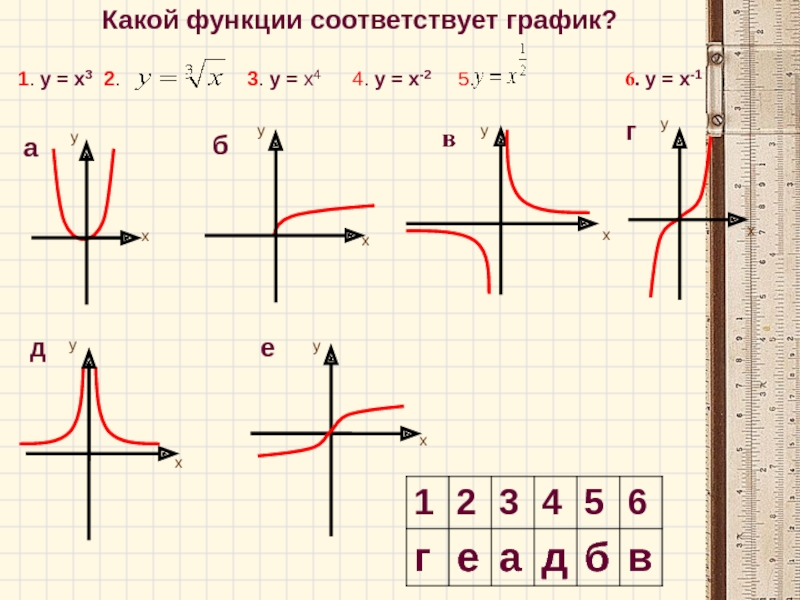
- 6. Какой график соответствует функции?
- 7. Какой функции соответствует график?
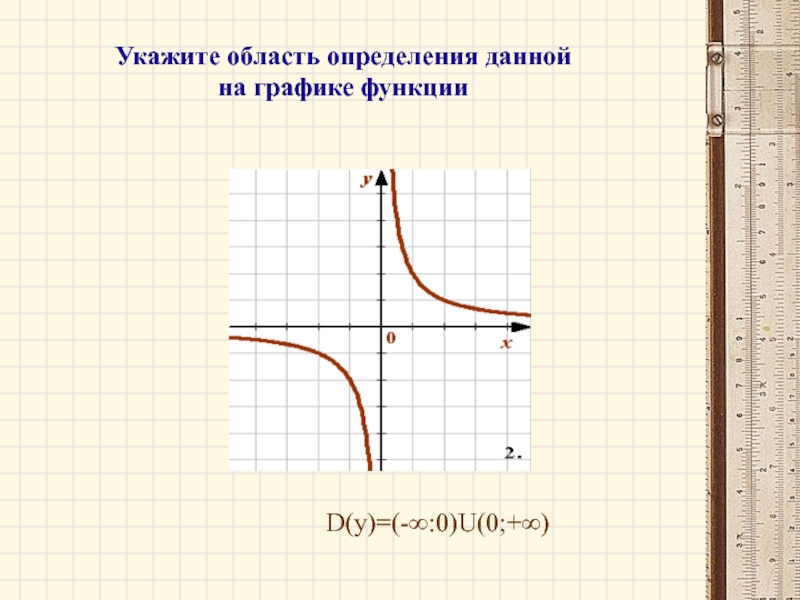
- 8. Укажите область определения данной на графике функцииD(y)=(-∞:0)U(0;+∞)
- 9. Укажите область определения данной на графике функцииD(y)=[-4;2]
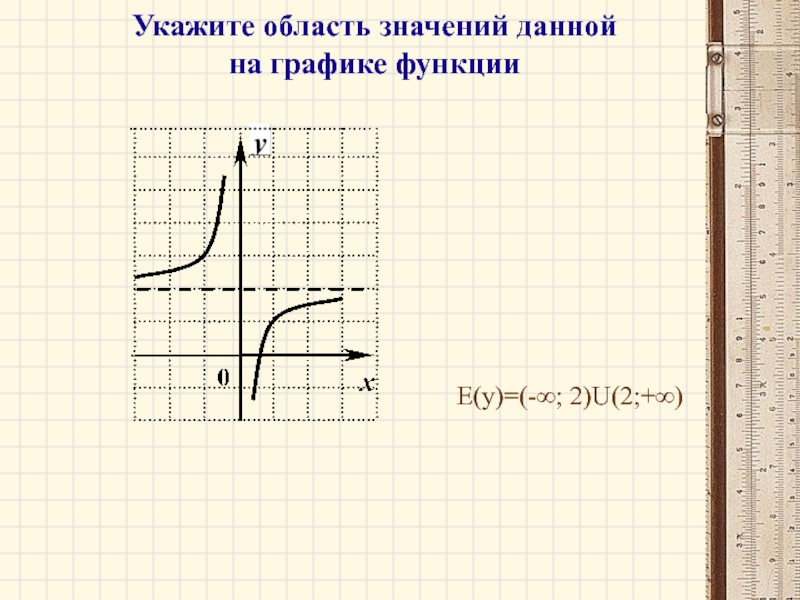
- 10. Укажите область значений данной на графике функции Е(y)=(-∞; 2)U(2;+∞)
- 11. Дано:Найти функцию, обратную данной у = g(x)
- 12. ххуу0022D(у)= (-∞;2) ∪ (2;+∞)Е(у)=(-∞;0)∪(0;+∞)D(у)= (-∞;0)∪(0;+∞)2. Е(у)= (-∞;2)∪(2;+∞)Найти область определения и множество значений для данных функций.
- 13. Свойства обратных функций. Область определения обратной функции
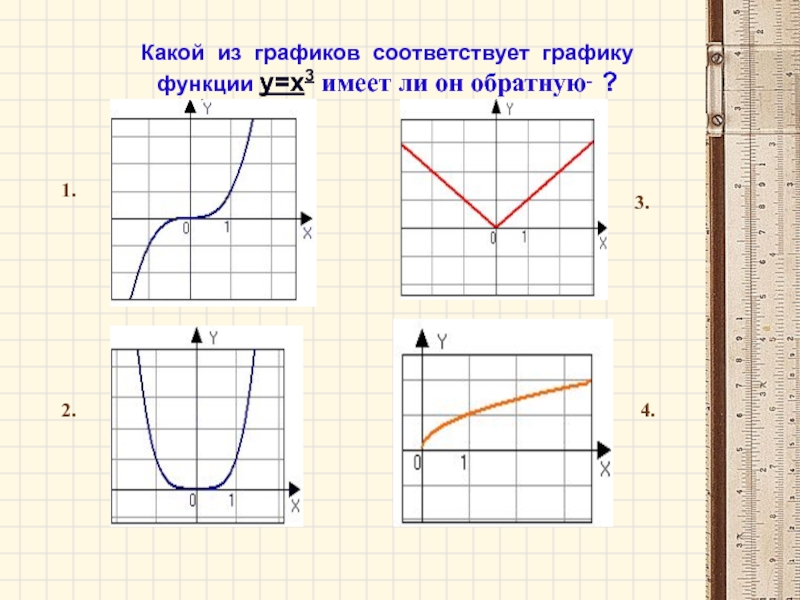
- 14. Дано: у = х3Построить график данной функции, выразите формулу функции обратной данной и постройте её график.Решение:ух0
- 15. 3. Если функция имеет обратную, то график
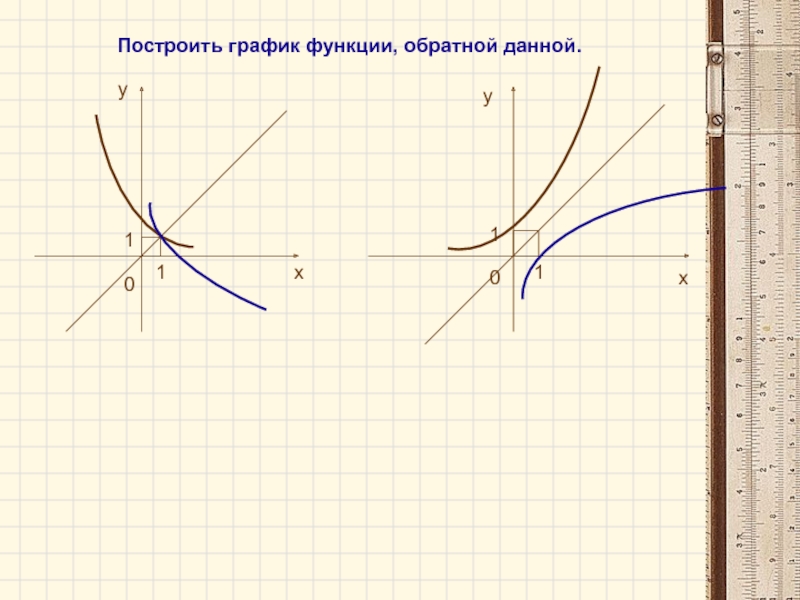
- 16. 111100хуух Построить график функции, обратной данной.
- 17. Обучающая самостоятельная работаI вариантНайти функцию,
- 18. ОтветыI вариантУ=2. D(y)=(-∞;+∞) Е(y)=(-∞;+∞)3. II вариантУ= 2. D(y)=(-∞;+∞) Е(y)=(-∞;+∞)3. ..ухху..00-213-2133-х4..2-х7
- 19. Задание на дом:П.2, решить № 579, № 576(в,гпо желанию №581(1,2)
- 20. На
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 11Дано:
Найти функцию, обратную данной у = g(x)
Решение:
Ответ:
Если функция (2) обратна к функции (1),
то такие функции называют взаимно-обратными.(1)
(2)
Слайд 12
х
х
у
у
0
0
2
2
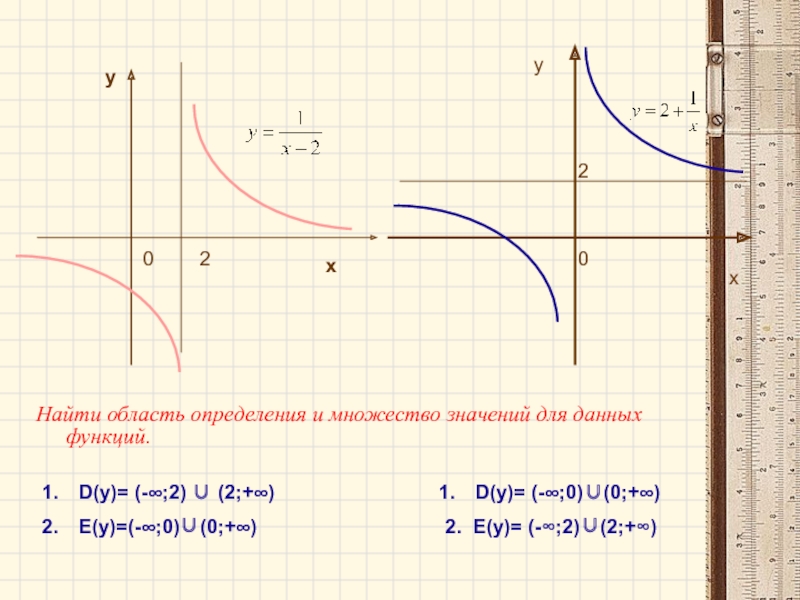
D(у)= (-∞;2) ∪ (2;+∞)
Е(у)=(-∞;0)∪(0;+∞)
D(у)= (-∞;0)∪(0;+∞)
2. Е(у)= (-∞;2)∪(2;+∞)
Найти область определения и
множество значений для данных функций.
Слайд 13Свойства обратных функций.
Область определения обратной функции g(x) совпадает с
множеством значений исходной функции f(x), а множество значений обратной функции
g(x) совпадает с областью определения исходной функции f(x):D(g(x) ) = E(f(x)), E(g(x)) = D(f(x)).
Монотонная функция является обратимой:
если функция f(x) возрастает, то обратная к ней функция g(x) также возрастает;
Если функция f(x) убывает, то обратная к ней функция g(x) также убывает.
Слайд 14
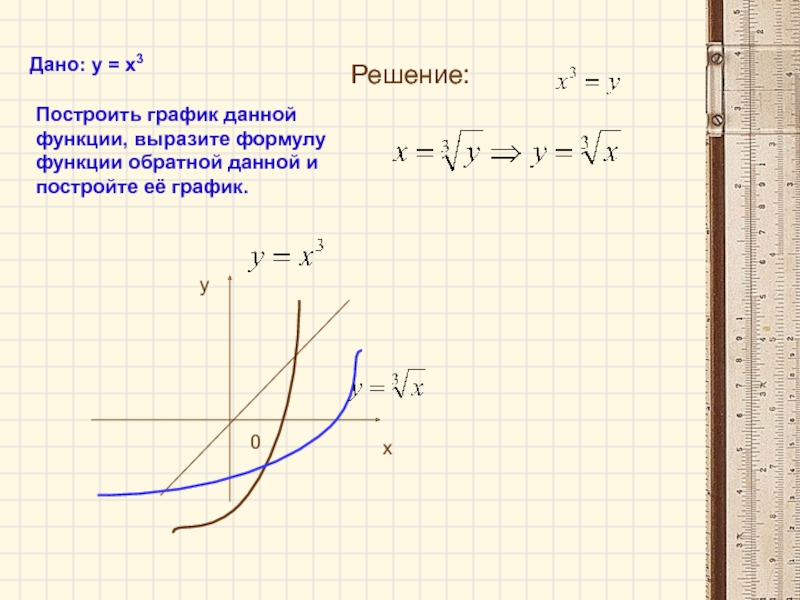
Дано: у = х3
Построить график данной функции, выразите формулу функции
обратной данной и постройте её график.
Решение:
у
х
0
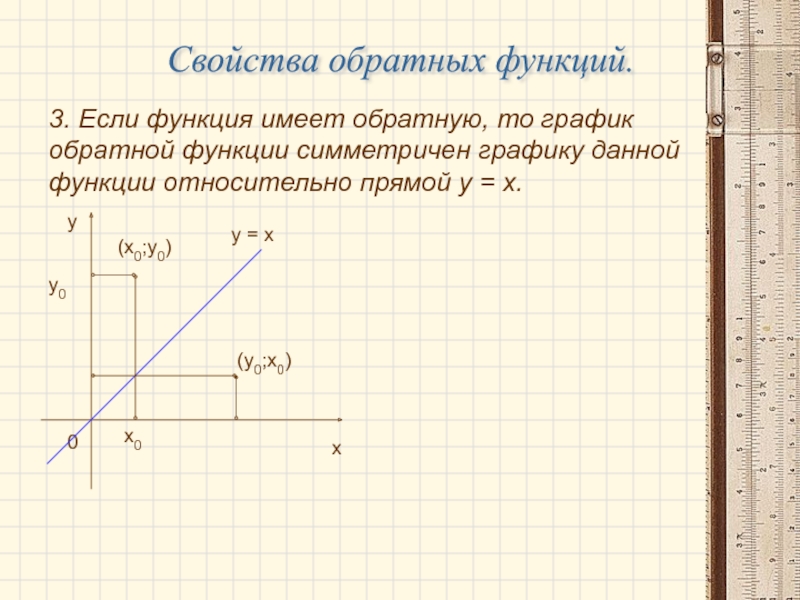
Слайд 153. Если функция имеет обратную, то график обратной функции симметричен
графику данной функции относительно прямой у = х.
х
у
0
(х0;у0)
х0
у0
(у0;х0)
у = х
Свойства
обратных функций. Слайд 17
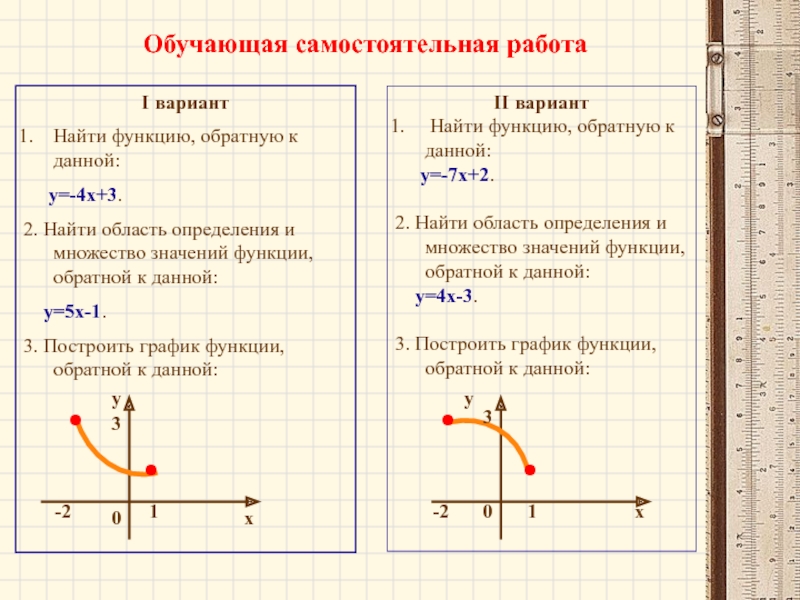
Обучающая самостоятельная работа
I вариант
Найти функцию, обратную к данной:
у=-4х+3.
2. Найти область определения и множество значений
функции, обратной к данной: у=5х-1.
3. Построить график функции, обратной к данной:
II вариант
Найти функцию, обратную к данной:
у=-7х+2.
2. Найти область определения и множество значений функции, обратной к данной:
у=4х-3.
3. Построить график функции, обратной к данной:
.
.
у
х
х
у
.
.
0
0
-2
1
3
-2
1
3
Слайд 18
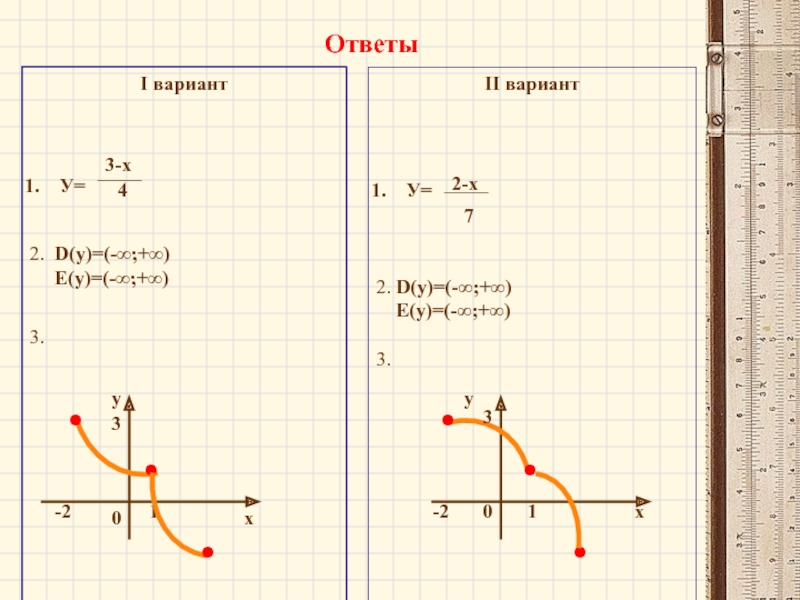
Ответы
I вариант
У=
2. D(y)=(-∞;+∞)
Е(y)=(-∞;+∞)
3.
II вариант
У=
2. D(y)=(-∞;+∞)
Е(y)=(-∞;+∞)
3.
.
.
у
х
х
у
.
.
0
0
-2
1
3
-2
1
3
3-х
4
.
.
2-х
7
Слайд 20
На уроке
я научился(лась)………………………….
На уроке мне интересно было …………………....
Трудно было ………………………………………….
Знания, полученные
на уроке, я могу использовать …………………………………………Р е ф л е к с и я:



![Взаимно обратные функции Укажите область определения данной на графике функцииD(y)=[-4;2] Укажите область определения данной на графике функцииD(y)=[-4;2]](/img/thumbs/3dd87da77cd6ccf837f71fcae1b46b24-800x.jpg)