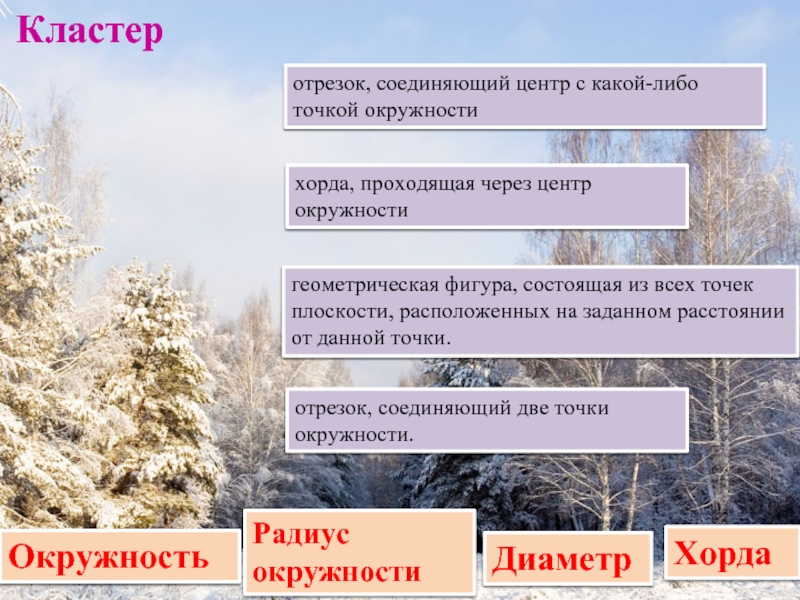
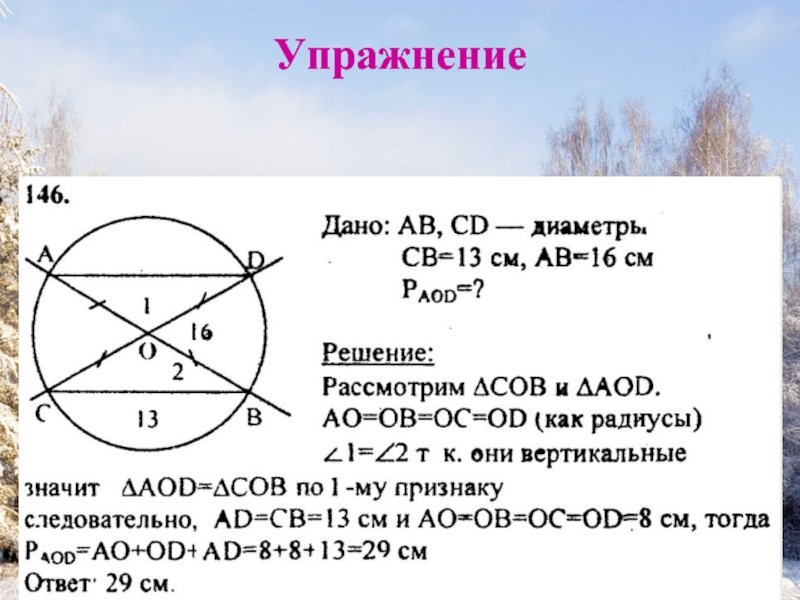
заданном расстоянии от данной точки.
Радиус окружности
отрезок, соединяющий центр с
какой-либо точкой окружностиотрезок, соединяющий две точки окружности.
Хорда
хорда, проходящая через центр окружности
Диаметр
Кластер