Задачи на построение сечений тетраэдра и параллелепипеда 10 класс

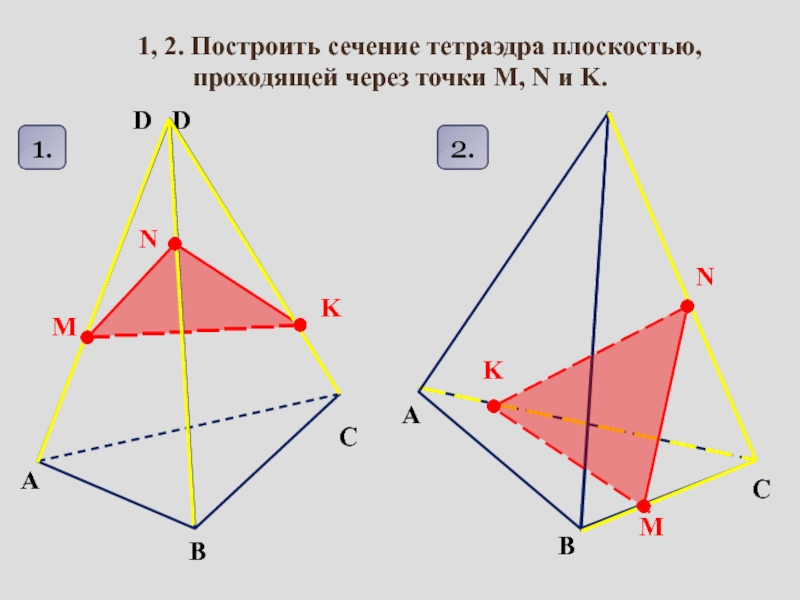
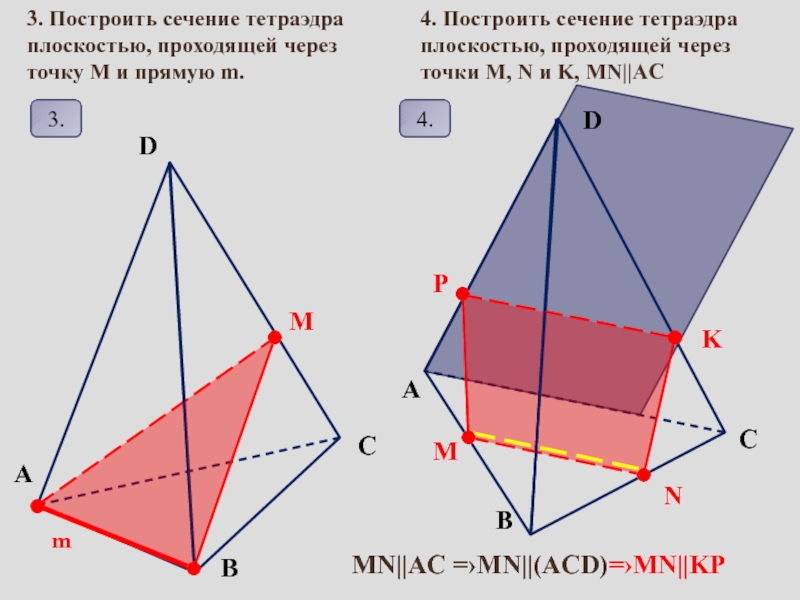
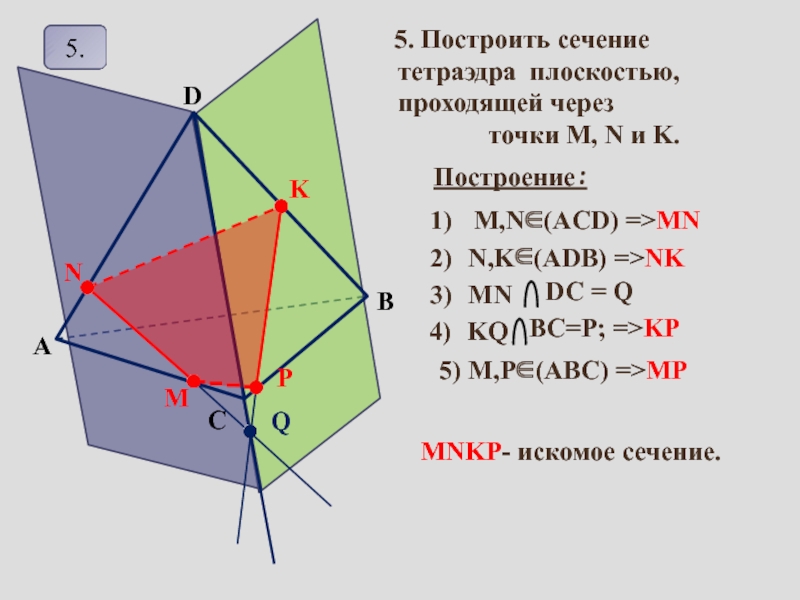
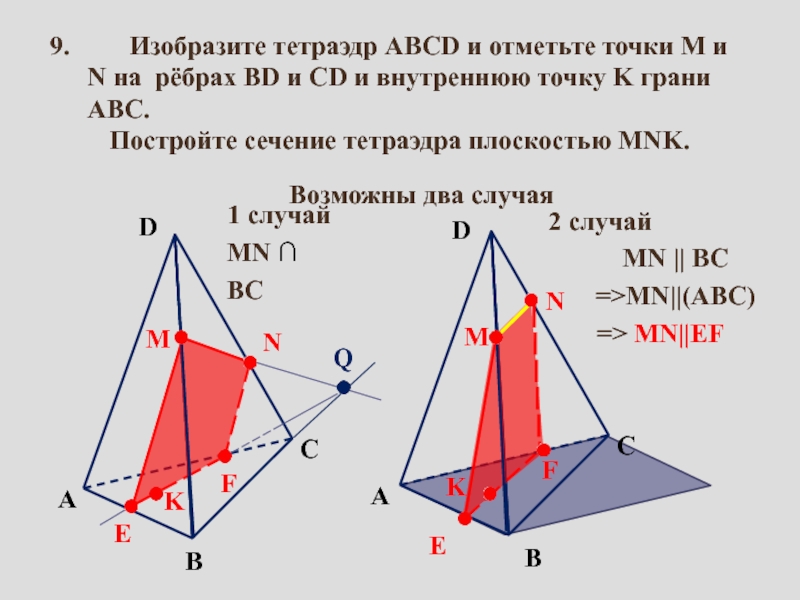
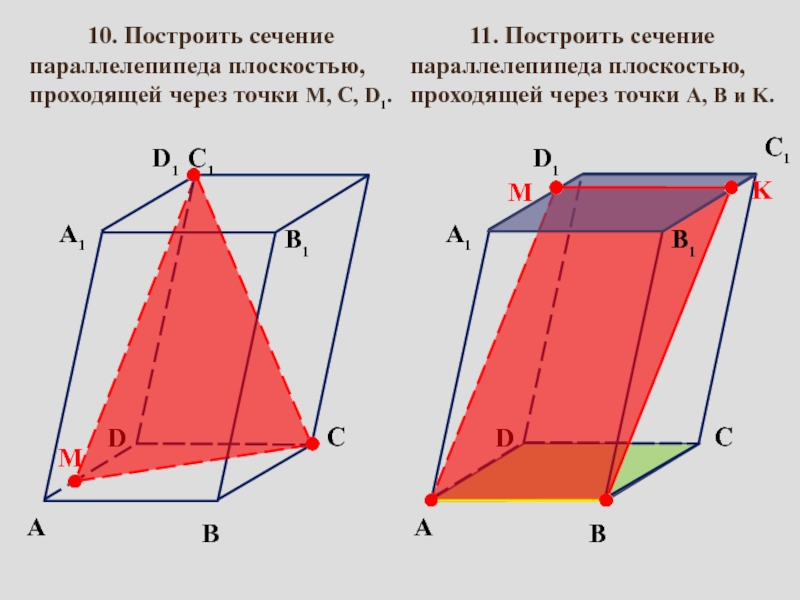
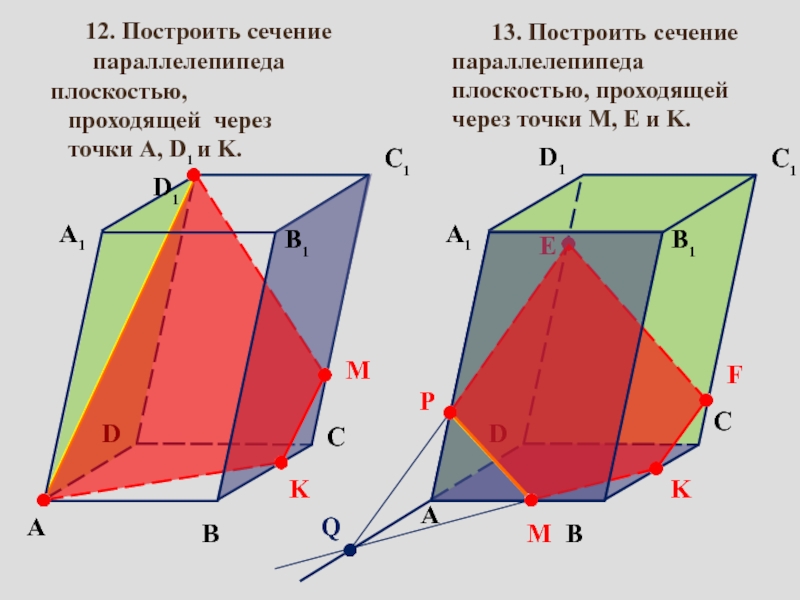
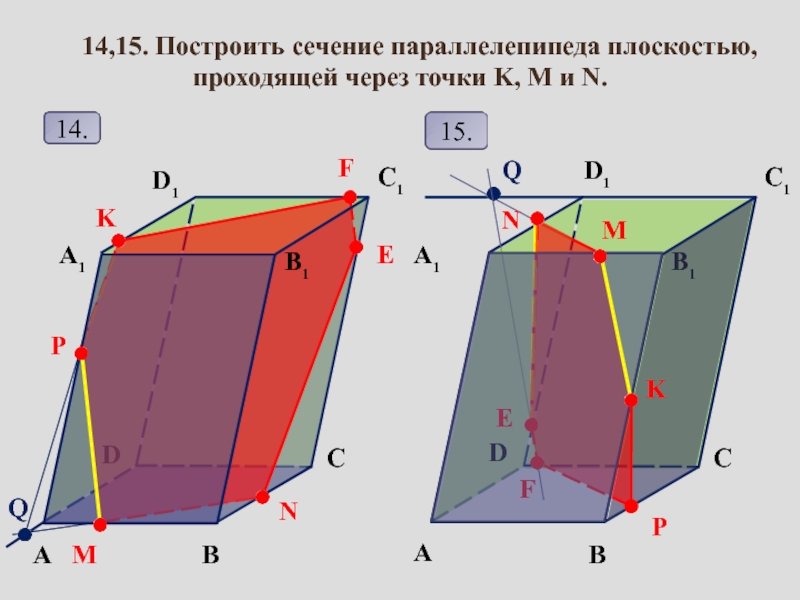
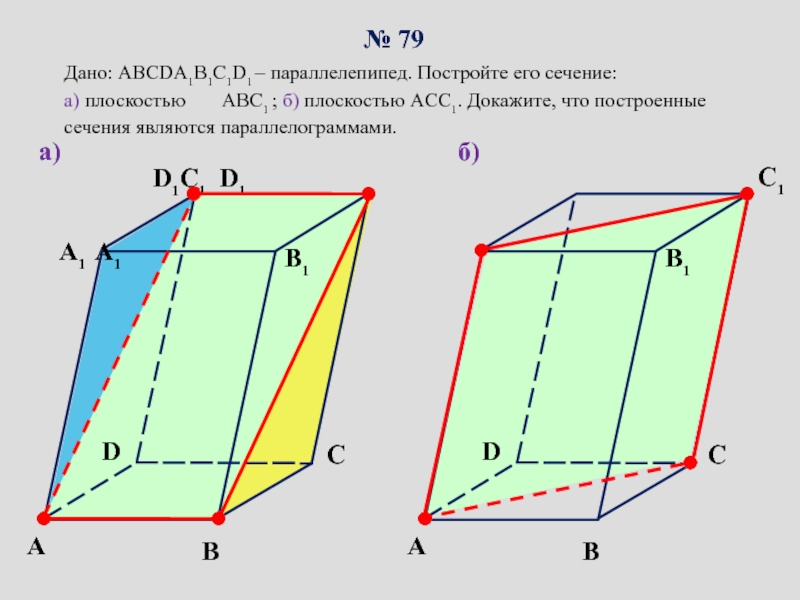
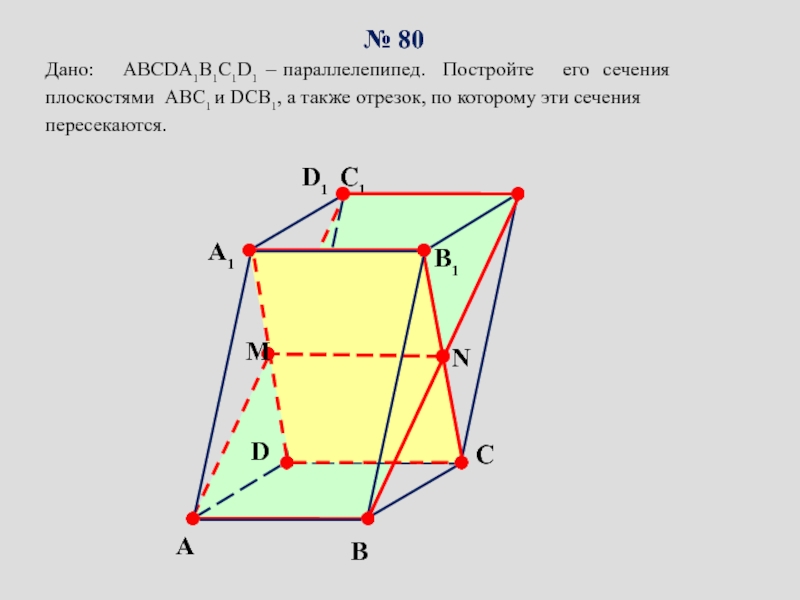
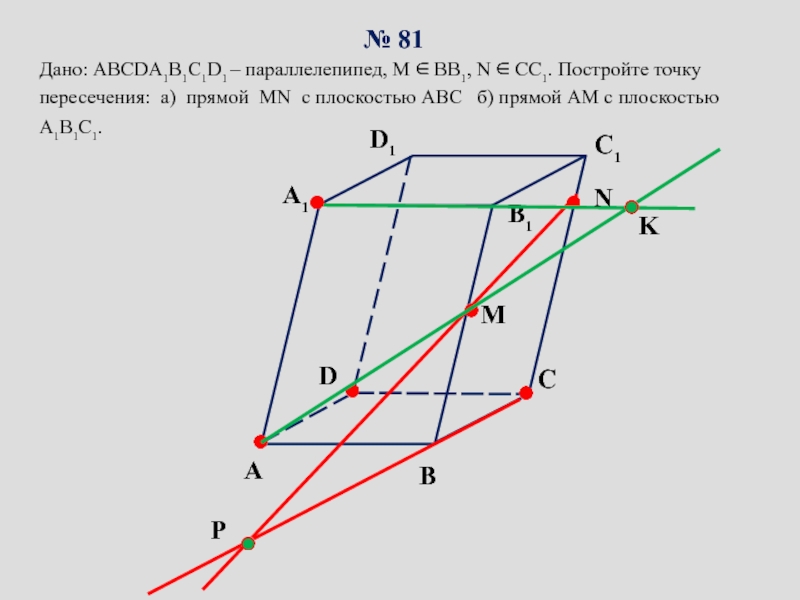
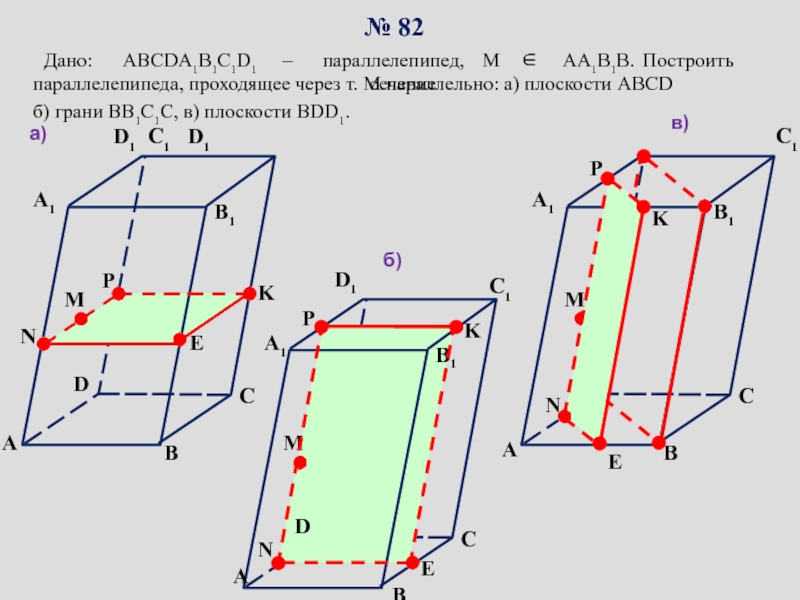
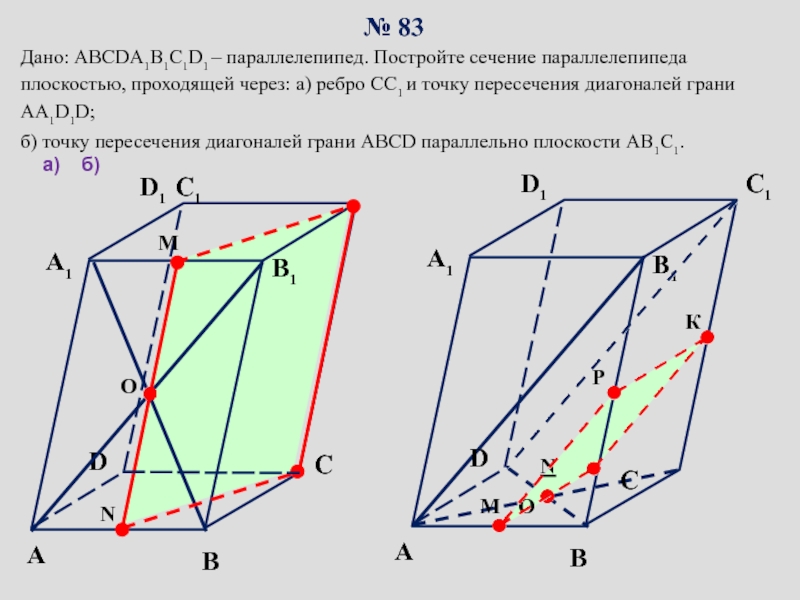
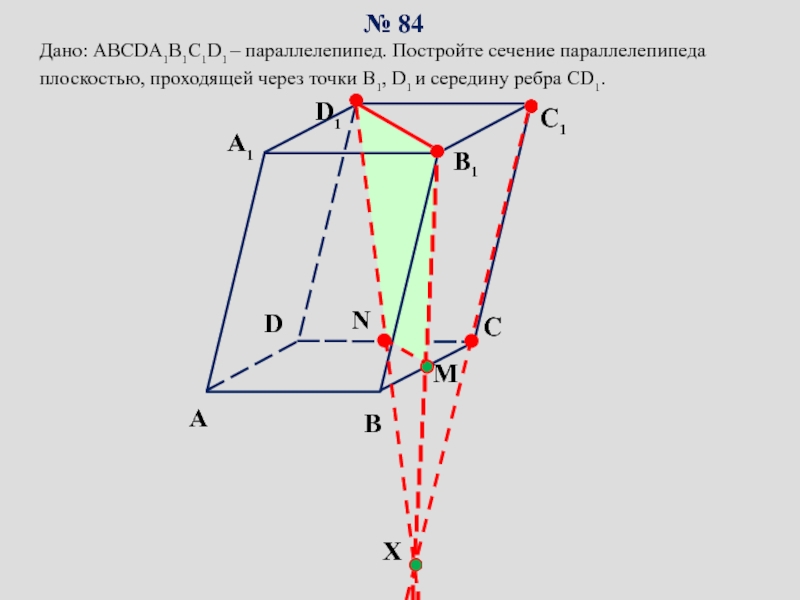
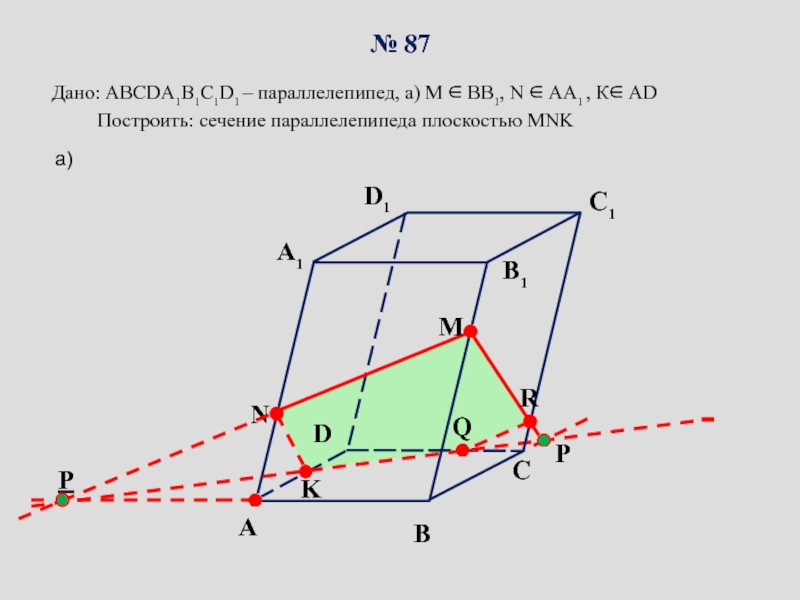
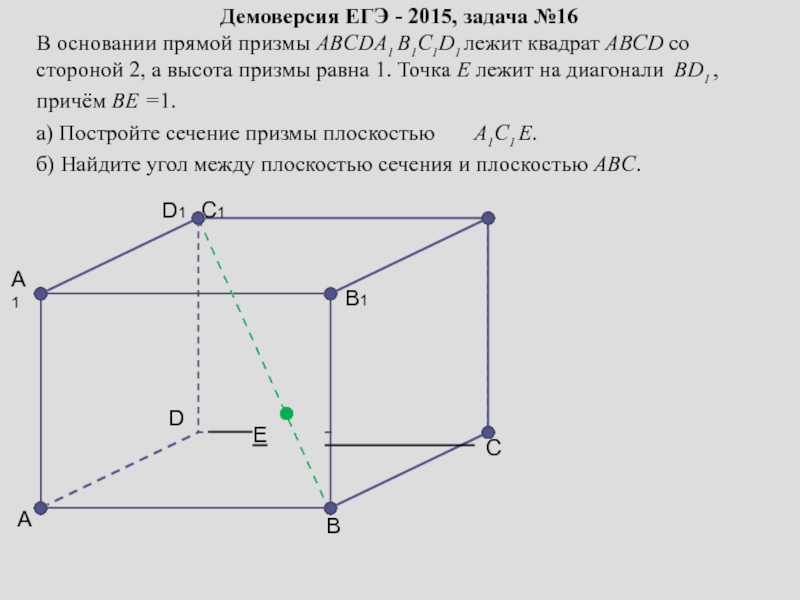
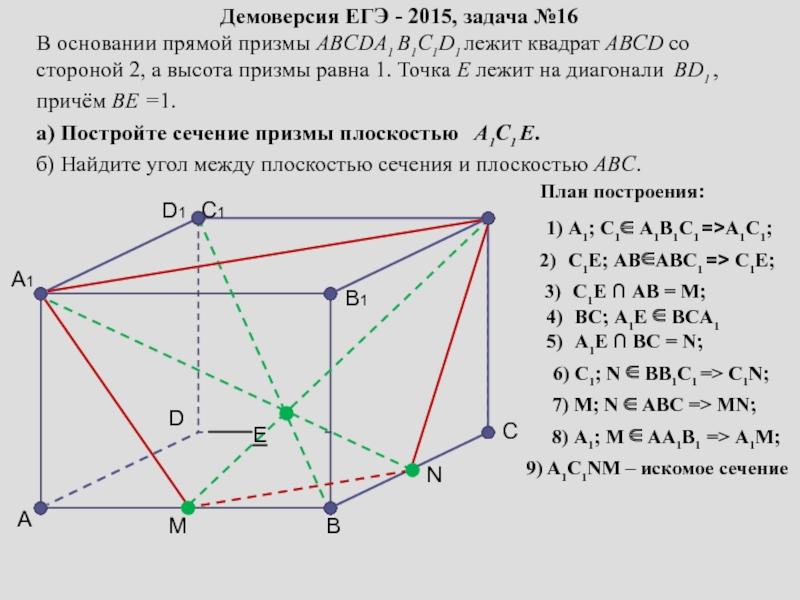
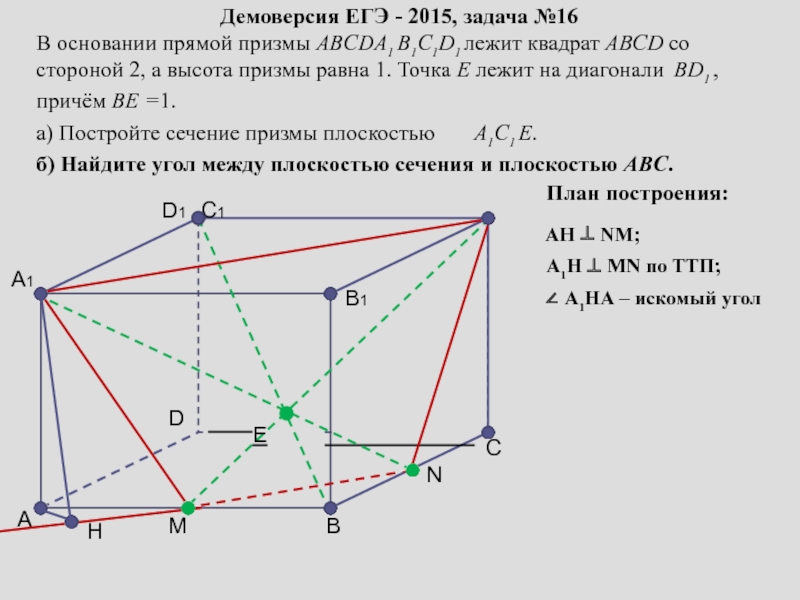
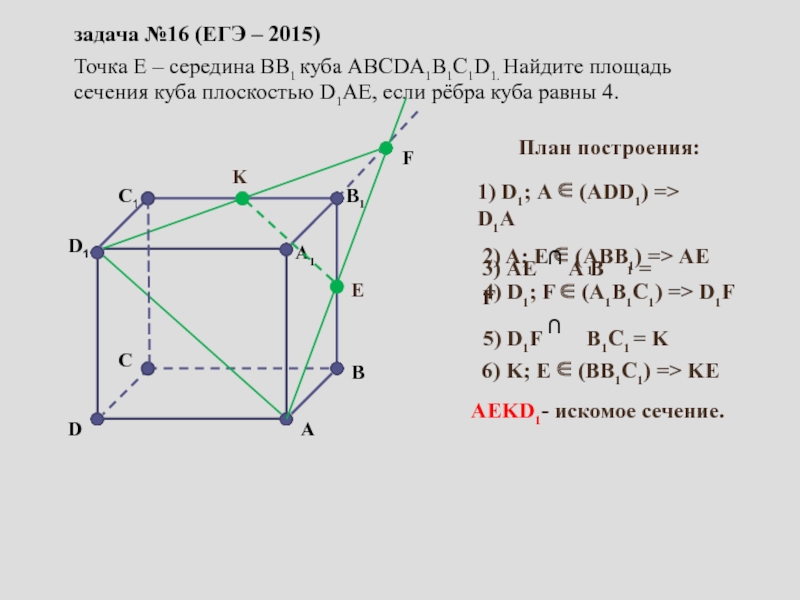
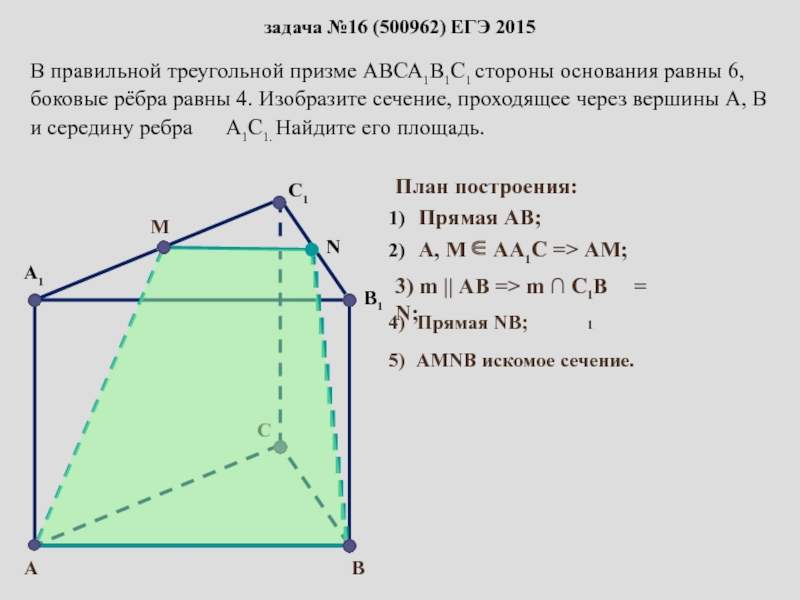
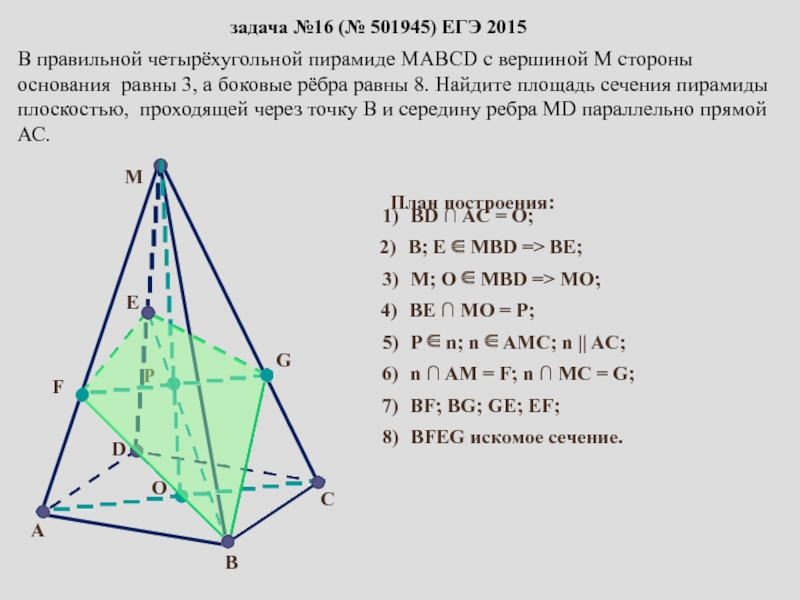
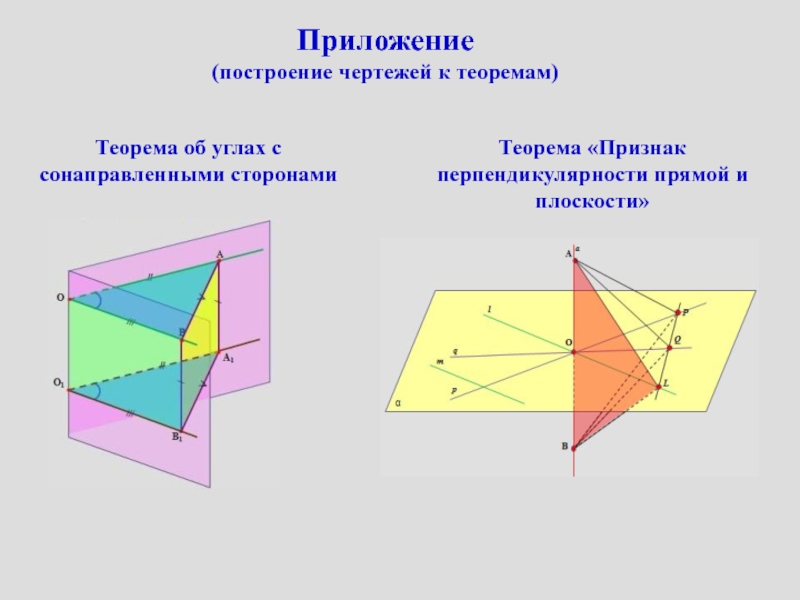
сопровождение изучения темы «Задачи на построение сечений
тетраэдра и параллелепипеда»

Геометрия 10

Конкурс педагогического мастерства – 2015 Номинация «Лучшая методическая разработка»

N и K.
A
B
C
M
N
K
A
B
C
D D
M
N
K
1.
2.

прямую m.
A
B
C
D
A
B
C
D
M
N
K
MN||AC =›MN||(ACD)=›MN||KP
P
M
m
4. Построить сечение тетраэдра плоскостью, проходящей через точки

3.

4.

и K.
Построение:
M,N(ACD) =>MN
N,K(ADB) =>NK
5) M,P(ABC) =>MP
MN
KQ
DC = Q BC=P; =>KP
MNKP-

и K.
A
B
C
D
K
Q
Q
Возможен другой способ построения?
N
P
M
6.

K.
A
B
C
D
A
B
C
D
K
N
M
P
Q
M
N
K
Q
P
7.
8.

рёбрах BD и CD и внутреннюю точку K грани ABC.
Постройте

A

B

C

K

N

M

1 случай MN ∩ BC

2 случай
MN || BC

D

E

F

E

F

=>MN||(ABC)
=> MN||EF

D1.
B
A
C
D
A1
B1
D1 C1
D1
A1
M
11. Построить сечение параллелепипеда плоскостью, проходящей через точки A, B

C1 K

M

B1

K.
D1
A1
C1
A
A1
B1
C1
D
B1
M
K
13. Построить сечение параллелепипеда плоскостью, проходящей через точки M, E

K

E

Q

P

M B

F C

и N.
14.
15.
B
C
D1
A1
C1
B
A
C
D1
B1
C1
Q
A M
N
K
P
E A1
F
B1
Q
N
M
E D
K
P

Атанасян, В.Ф.
Бутузов и др.

б) плоскостью ACC1. Докажите, что построенные
сечения являются параллелограммами.

D1 C1 D1
а)
б)

по которому эти сечения пересекаются.
D
B
A
C
A1
B1
D1 C1
M
N

CC1. Постройте точку пересечения: а) прямой MN с плоскостью ABC б)

A1B1C1.

C

K

N

M

б) грани BB1C1C, в) плоскости BDD1.
M
M
M
N
P
K
E
N
A
N
P
P
K
K
E
E
а)
б)
в)

через: а) ребро СС1 и точку пересечения диагоналей грани AА1D1D;
б)

B

A

D1

A1

B1

C1

О

D1 C1
М

N

D
М

N C
О

Р

К

а) б)

через точки B1, D1 и середину ребра CD1.
C
X
M

где точка К – середина ребра АA1, а точка L

Докажите, что построенное сечение параллелограмм.

D

B

A

C

D1

A1

B1

C1

L

К

X

Y

через диагональ АС основания параллельно диагонали ВD1.
D
B
A
C
A1
B1
D1 C1
К

 АА1 , К АD Построить: сечение параллелепипеда плоскостью MNK
C
а)
N
M
K
P
Q
P
R

E C

Демоверсия ЕГЭ - 2015, задача №16
В основании прямой призмы ABCDA1 B1C1D1 лежит квадрат ABCD со

стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1 , причём BE =1.
а) Постройте сечение призмы плоскостью A1C1 E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.

Демоверсия ЕГЭ - 2015, задача №16
В основании прямой призмы ABCDA1 B1C1D1 лежит квадрат ABCD со

E

M

N

стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1 , причём BE =1.
а) Постройте сечение призмы плоскостью A1C1 E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
План построения:

1) А1; С1 А1В1С1 =>А1С1;
С1Е; ABАBC1 => С1E;
С1Е ∩ АВ = М;
BC; А1Е  BCA1
А1Е ∩ ВС = N;
6) С1; N  BB1C1 => С1N;
7) M; N  ABC => MN;
8) А1; M  AA1B1 => А1M;
9) A1C1NM – искомое сечение

B1C1D1 лежит квадрат ABCD со
A
A1
B
D
B1
D1 C1

E C

M

N

Н

стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1 , причём BE =1.
а) Постройте сечение призмы плоскостью A1C1 E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
План построения:

АН  NМ;
А1Н  МN по ТТП;
 А1НА – искомый угол

ABCDA1B1C1D1. Найдите площадь
сечения куба плоскостью D1AЕ, если рёбра куба равны

А

C

1

D

В

1

А1

В

D

1

F

План построения:

1) D1; А  (АDD1) => D1А
2) A; Е  (АВВ1) => АЕ

1 1
4) D1; F  (А1В1C1) => D1F

K

C

Е

3) АЕ ∩ А В = F

5) D1F ∩ В1C1 = K
6) K; Е  (ВВ1C1) => KЕ
AEKD1- искомое сечение.

основания равны 6, боковые рёбра равны 4. Изобразите сечение, проходящее

A

B

C

A1

B1

C1

M

N

План построения:
Прямая АВ;
А, М  АА1С => АМ;

1 1

3) m  АВ => m ∩ C B = N;

Прямая NВ;
AMNB искомое сечение.

с вершиной М стороны основания равны 3, а боковые рёбра

BD ∩ AC = O;
B; E  MBD => BE;
M; O  MBD => MO;
BE ∩ MO = P;
P  n; n  AMC; n  AC;
n ∩ AM = F; n ∩ MC = G;
BF; BG; GE; EF;
BFEG искомое сечение.

перпендикулярности прямой и плоскости»