Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Золотое сечение-гармония математики
Содержание
- 1. Золотое сечение-гармония математики
- 2. Содержание:ВступлениеИстория «Золотого сечения»Математическое понимание гармонииПонятие «Золотое сечение»«Золотое сечение» - гармония математикиЗолотое сечение в геометрии Вывод
- 3. ВступлениеВ дошедшей до нас античной литературе золотое
- 4. История «Золотого сечения»В Древнем Египте существовала «система
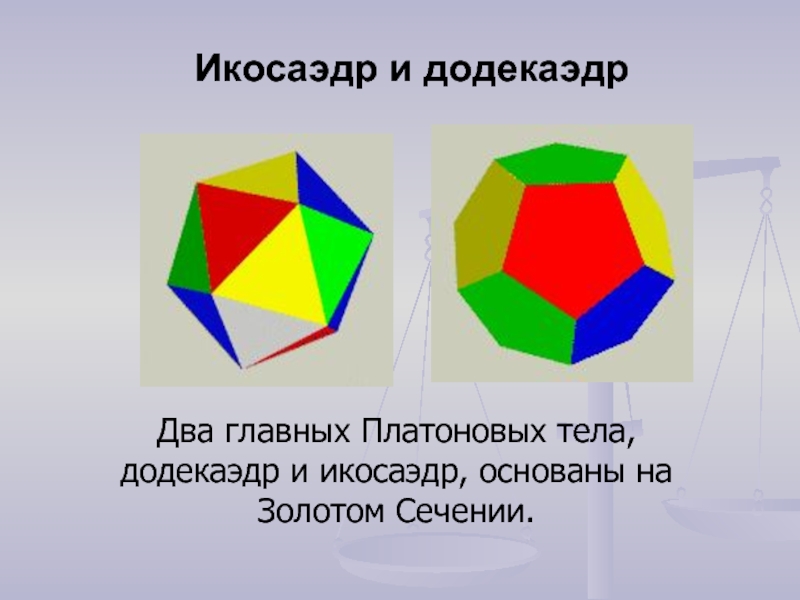
- 5. Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении.Икосаэдр и додекаэдр
- 6. Ряд ФибоначчиС историей золотого сечения связано имя
- 7. «Золотая Пропорция» - главный эстетический принцип эпохи
- 8. «Витрувийский человек» Леонардо да ВинчиРазрабатывая правила
- 9. Вклад Кеплера в теорию Золотого СеченияГениальный
- 10. Математическое понимание гармонии«Гармония – соразмерность частей и
- 11. Понятие «Золотое сечение»a : b = b
- 12. Эта пропорция равна: Золотое сечение в процентах
- 13. Число j является положительным корнем квадратного уравнения:x2
- 14. Дано: отрезок АВ.Построить: золотое сечение отрезка
- 15. АВСЗолотым называется такой равнобедренный треугольник, основание и
- 16. Прямоугольник, стороны которого находятся в золотом отношении,
- 17. Последовательно отрезая от золотого прямоугольника квадраты и
- 18. ПентаграммаЕсли в пентаграмме провести все диагонали, то
- 19. ВыводЦелое всегда состоит из частей, части разной
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Золотое сечение -
Учитель математики МОУ СОШ № 4 с углубленным
изучением отдельных предметов Прийма Т.Б.
Слайд 2Содержание:
Вступление
История «Золотого сечения»
Математическое понимание гармонии
Понятие «Золотое сечение»
«Золотое сечение» - гармония
математики
Золотое сечение в геометрии
Вывод
Слайд 3Вступление
В дошедшей до нас античной литературе золотое деление впервые упоминается
в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение
золотого деления. После Евклида исследованием золотого деления занимались многие ученые. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.Что же такое «золотое сечение»?
Слайд 4История «Золотого сечения»
В Древнем Египте существовала «система правил гармонии», основанная
на Золотом Сечении.
В Древней Греции Золотое Сечение было своеобразным
каноном культуры, который пронизывает все сферы науки и искусства. Красота и гармония стали важнейшими категориями познания. В толковании древних греков понятие золотого сечения, и понятие гармонии идентичны.
Согласно Пифагору гармония имеет численное выражение, то есть, она связана с концепцией числа.
Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения.
Теория гармонии Древних
Слайд 5Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом
Сечении.
Икосаэдр и додекаэдр
Слайд 6Ряд Фибоначчи
С историей золотого сечения связано имя итальянского математика Леонардо
Фибоначчи.
Ряд чисел 0, 1, 1, 2, 3, 5, 8,
13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Каждый член последовательности, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления.
Все исследователи золотого деления в растительном и в животном мире, искусстве, неизменно приходили к ряду Фибоначчи как арифметическому выражению закона золотого деления.
Слайд 7«Золотая Пропорция» - главный эстетический принцип эпохи Средневековья
Эпоха Возрождения ассоциируется
с именами таких «титанов», как Леонардо да Винчи, Микеланджело, Рафаэль,
Николай Коперник, Альберт Дюрер, Лука Пачоли.Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение».
Доказано, что во многих своих произведениях Леонардо да Винчи использовал пропорции золотого сечения, в частности, в своей всемирно известной фреске «Тайная вечеря» и непревзойденной «Джоконде.
Слайд 8«Витрувийский человек»
Леонардо да Винчи
Разрабатывая правила изображения человеческой фигуры, Леонардо
да Винчи пытался на основе литературных сведений древности восстановить так
называемый «квадрат древних».Он выполнил рисунок, в котором показано, что размах вытянутых в сторону рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и в круг.
При исследовании рисунка можно заметить, что комбинация рук и ног в действительности составляет четыре различных позы.
Рисунок и текст иногда называют каноническими пропорциями.
Слайд 9Вклад Кеплера
в теорию Золотого Сечения
Гениальный астроном Иоганн Кеплер (1571-1630)
был последовательным приверженцем Золотого Сечения, Платоновых тел и Пифагорейской доктрины
о числовой гармонии Мироздания.Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:
1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;…в пределе стремится к золотой пропорции
Слайд 10Математическое понимание гармонии
«Гармония – соразмерность частей и целого, слияние различных
компонентов объекта в единое органическое целое. В гармонии получают внешнее
выявление внутренняя упорядоченность и мера бытия» -Большая Советская ЭнциклопедияМатематическая гармония - это равенство или соразмерность частей с друг другом и части с целым.
Понятие математической гармонии тесно связано с понятиями пропорции и симметрии.
Слайд 11Понятие «Золотое сечение»
a : b = b : c
или с : b = b :
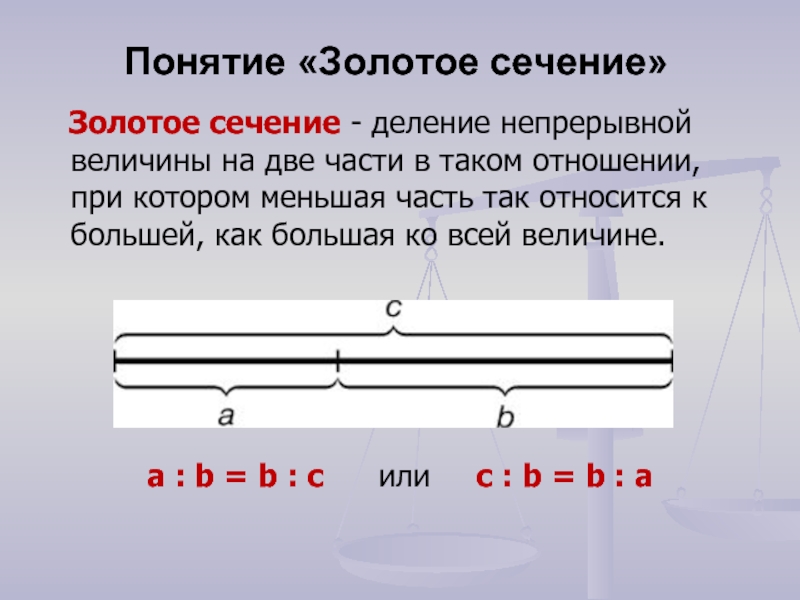
а Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Слайд 13Число j является положительным корнем квадратного уравнения:
x2 = x +
1
подставим корень j вместо x и разделим на
j : Если продолжить такую подстановку бесконечное число раз, то получим цепную дробь:
Аналогично, если взять корень квадратный из правой и левой частей тождества (1) то получим представление золотой пропорции в «радикалах»:
(2)
(3)
(1)
(4)
Эти формулы (3) и (4) доставляют «эстетическое наслаждение» и вызывают неосознанное чувство ритма и гармонии…
«Золотое сечение» - гармония математики
Слайд 14 Дано: отрезок АВ.
Построить: золотое сечение отрезка АВ, т.е. точку
Е так, чтобы
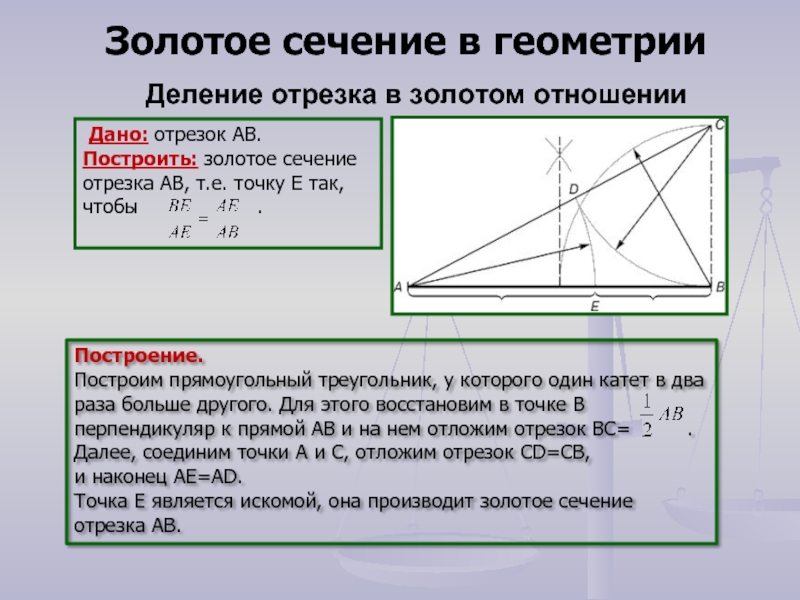
.Построение.
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= .
Далее, соединим точки А и С, отложим отрезок CD=CB,
и наконец AE=AD.
Точка Е является искомой, она производит золотое сечение отрезка АВ.
Деление отрезка в золотом отношении
Золотое сечение в геометрии
Слайд 15А
В
С
Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого
находятся в золотом отношении:
Золотой треугольник
Слайд 16Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины
к ширине даёт число φ, называется золотым прямоугольником.
Золотой прямоугольник
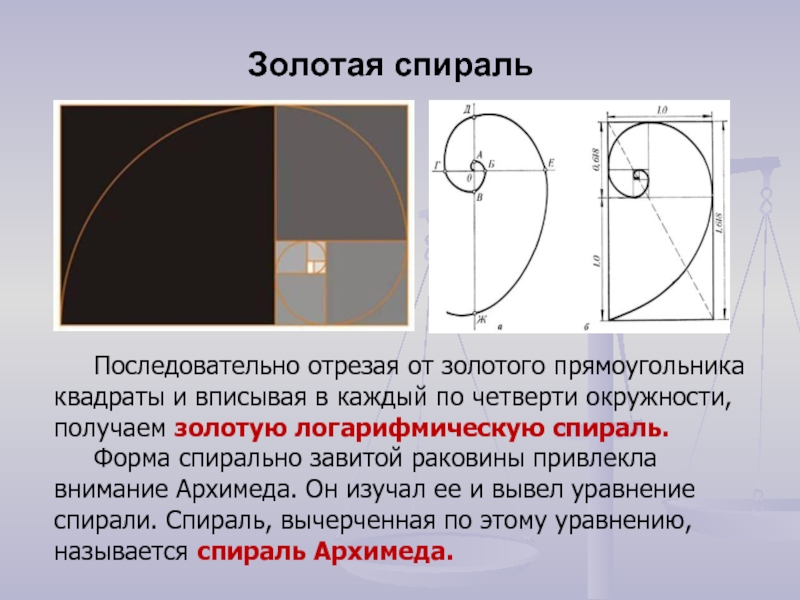
Слайд 17Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый
по четверти окружности, получаем золотую логарифмическую спираль.
Форма спирально завитой раковины
привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда.Золотая спираль
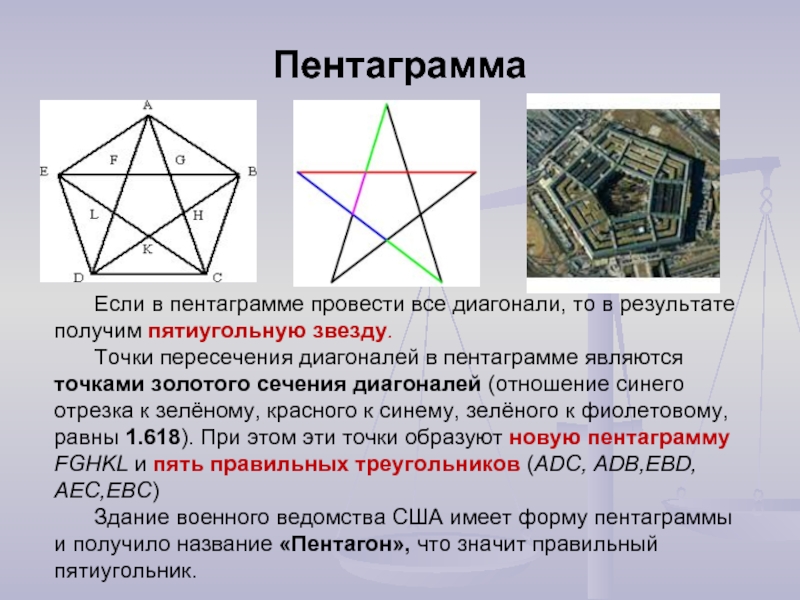
Слайд 18Пентаграмма
Если в пентаграмме провести все диагонали, то в результате получим
пятиугольную звезду.
Точки пересечения диагоналей в пентаграмме являются точками золотого
сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC) Здание военного ведомства США имеет форму пентаграммы и получило название «Пентагон», что значит правильный пятиугольник.