Слайд 1Текстовая задача и процесс ее решения
Слайд 2ЛИТЕРАТУРА:
Справочник учителя начальной школы. Математика/ А.С. Добротворский, Л.П. Ковригина,
И.С. Ордынкина и др. – М. : Дрофа, 2007. –
158 с.
Баймарукова П.У. Методика обучения математике в начальных классах/ П.У. Байрамукова, А.У. Уртенова – Ростов н/Д : Феникс, 2009. – 299 с.
Белошистая А. В. Методика обучения математике в начальной школе: курс лекций: учебное пособие для студентов вузов, обучающихся по спец. «Педагогика и методика начального образования». – М. : ВЛАДОС, -2007.- 455с.
Калиниченко А. В. Методика преподавания начального курса математики / А. В. Калиниченко, Р. Н. Шикова, Е. Н. Леонович. – М. : Академия, 2013. – 208 с.
Слайд 3ПЛАН ЛЕКЦИИ
Понятие «текстовая задача».
Моделирование в процессе решения текстовых задач.
Методы и
способы решения текстовых задач.
Формы записи решения задач.
Этапы решения текстовой задачи
и приемы их выполнения.
Слайд 41. Понятие «текстовая задача»
Понятие задача относится к числу общенаучных.
В
начальном курсе математики понятие задача используется тогда, когда идет речь
об арифметических задачах, сформулированных в виде текста.
Такие задачи называются «текстовыми» или «сюжетными».
Слайд 5ТЕКСТОВАЯ ЗАДАЧА
УСЛОВИЕ
ТРЕБОВАНИЕ
Слайд 6В условии задачи указываются связи между данными числами, а также
между данными и искомым – эти связи определяют
выбор арифметических
действий, необходимых для решения задачи.
Слайд 7«Решить задачу – значит раскрыть связи между данными и искомым,
заданных условием задачи, на основе чего выбрать, а затем выполнить
арифметические действия и дать ответ на вопрос задачи»
(М. А. Бантова, Г. В. Бельтюкова).
Слайд 92. Моделирование в процессе решения текстовых задач
Модель – искусственно созданный
объект в виде схемы, чертежа, математической формулы, выражения, записи решения
и другого.
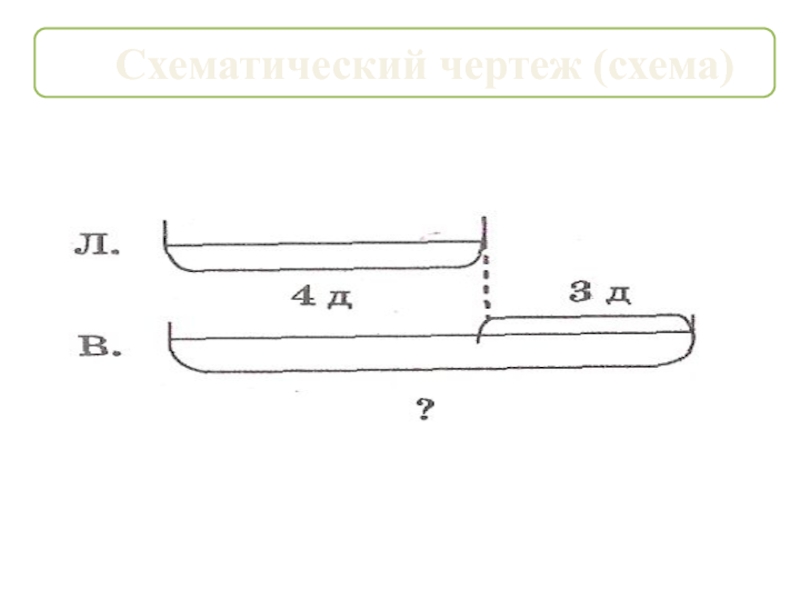
Слайд 10Например: «Лида нарисовала 4 домика, а Вова на 3 домика
больше. Сколько домиков нарисовал Вова?»
Рисунок:
Слайд 14Краткая запись задачи на естественном языке
Слайд 15Таблица
(задачи связанные с пропорциональными величинами)
Задача. 20 м ткани стоят 960
рублей. Сколько такой ткани можно купить на 288 рублей?
Слайд 16Так как модель – это своеобразная копия задачи, то на
ней должны быть представлены все ее объекты, все отношения между
ними, указаны требования.
Слайд 173. Методы и способы решения текстовых задач
Основными методами решения текстовых
задач являются алгебраический и арифметический.
Слайд 18Решить задачу арифметическим методом - это значит найти ответ на
требование задачи посредством
выполнения арифметических действий над числами.
Слайд 19Одну и ту же задачу можно решить различными арифметическими способами.
Они отличаются друг от друга логикой рассуждений, выполняемых в процессе
решения задачи.
Слайд 20Например:
Сшили 3 платья, расходуя на каждое по 4 м ткани.
Сколько кофт можно сшить из этой ткани, если расходовать на
одну кофту 2 м?
2 способ
1) 4 : 2 = 2 (раза) - во столько раз больше идет ткани на платье, чем на кофту;
2) 3 – 2 = 6 (к) - столько кофт можно сшить.
1 способ
1) 4 • 3=12 (м) - столько было ткани;
2) 12 : 2=6 (к) - столько кофт можно сшить из 12 м ткани.
Слайд 21Решить задачу алгебраическим методом - это значит найти ответ на
требование задачи, составив и решив уравнение или систему уравнений.
Если для
одной и той же задачи можно составить различные уравнения, то это означает, что данную задачу можно решить различными алгебраическими способами.
Слайд 22Задача. Свитер, шапку и шарф связали из 1 кг 200
г шерсти. На шарф потребовалась на 100 г больше, чем
на шапку, и на 400 г меньше, чем на свитер. Сколько грамм шерсти израсходовали на каждую вещь?
Эту задачу можно решить тремя различными способами.
Слайд 231 способ:
Обозначим через х (г) массу шерсти, израсходованной на шапку.
Тогда на шарф будет израсходовано (х +100) г, а на
свитер ((х + 100) + 400) г. Так как на все три вещи израсходовано 1 200 г, то можно составить уравнение.
х+(х+100)+((х+100)+400)=1 200
Выполнив преобразования, получим, что х = 200.
Таким образом, на шапку было израсходовано 200 г,
на шарф - 300 г, так как 200 + 100 = 300,
на свитер - 700 г.
Слайд 242 способ
Обозначим через х (г) массу шерсти, израсходованной на шарф.
Тогда на шапку будет израсходовано
(х - 100) г, а
на свитер - (х + 400) г. Поскольку на все три вещи израсходовано 1 200 г, то можно составить уравнение:
х + (х - 100) + (х + 400) = 1 200
Слайд 253 способ
Обозначим через х (г) массу шерсти, израсходованной на свитер.
Тогда на шарф будет израсходовано (х - 400) г,
а
на шапку - (х-400-100) г. Поскольку на все три вещи израсходовано 1 200 г, то можно составить уравнение; х+(х-400) +(х-400-100)=1 200
Выполнив преобразования, получим, что х=700. Таким образом, если на свитер израсходовано 700 г, то на шарф пошло 300 г, а на шапку - 200 г (700-400-100=200).
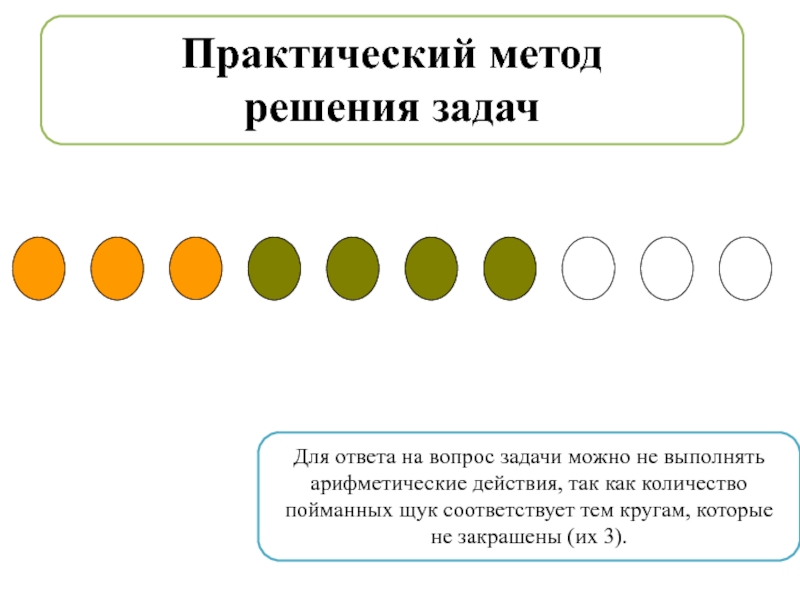
Слайд 26Задача. Рыбак поймал 10 рыб. Из них 3 леща, 4
окуня, остальные щуки. Сколько щук поймал рыбак?
Кроме арифметического и алгебраического
методов решения задач существуют еще практический и графический.
Слайд 27
Практический метод
решения задач
Для ответа на вопрос задачи можно не
выполнять арифметические действия, так как количество пойманных щук соответствует тем
кругам, которые не закрашены (их 3).
Слайд 28Графический метод решения задач
Этот способ так же как практический, позволяет
ответить на вопрос задачи, не выполняя арифметических действий.
лещи
окуни щуки