1 asym Kr RivShaмирAделм +4-mod33 7.ppt

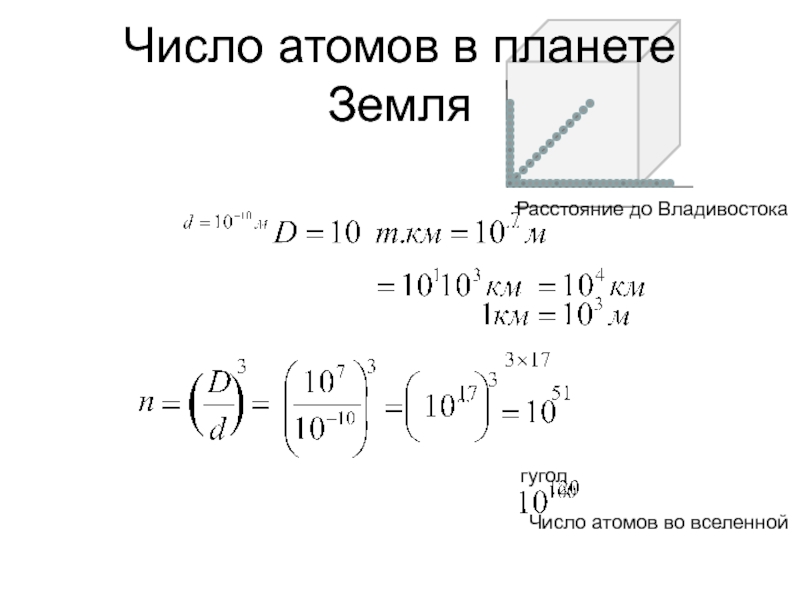
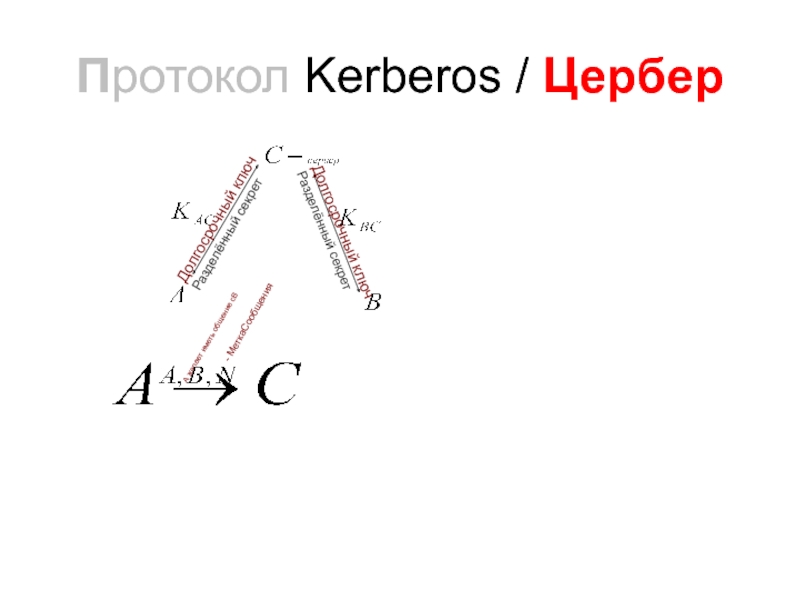
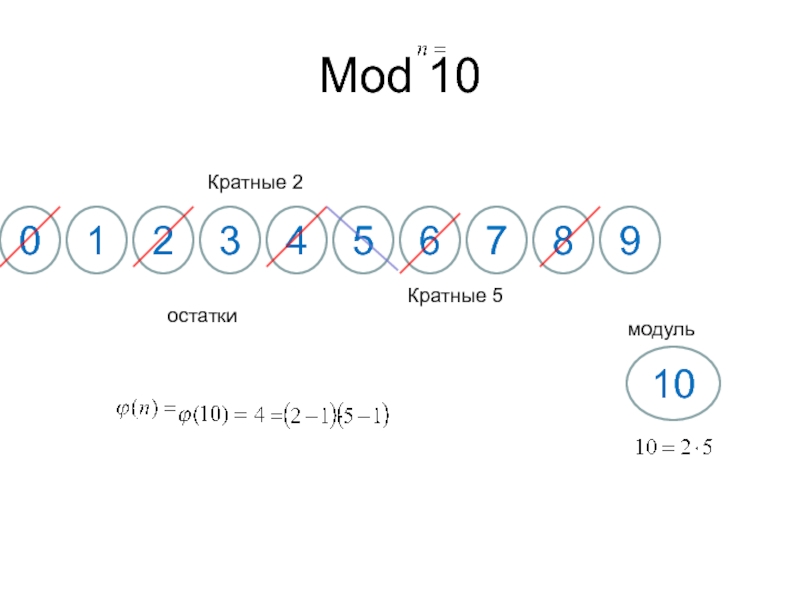
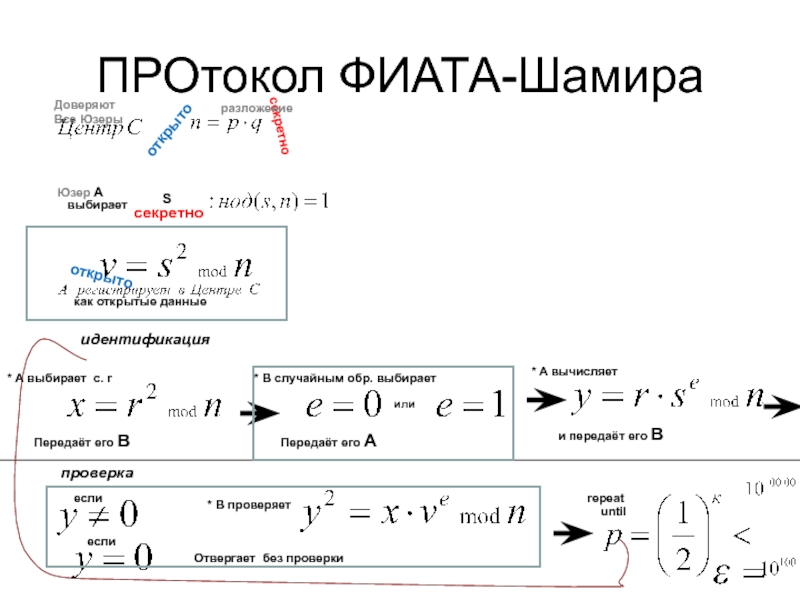
*24*3600секунд= 1018 секунд

Скорость света
С=300 тыс. м/сек=107 м/с

Размер Вселенной
L=c*T=107 м/с* 1018

с =1027 метров

Планковская длина l=(hG/c3)0,5=10-35 м (дано из внешнего источника)

Рассчитаем число Планковских длин вдоль Вселенной n=L/l=1062 штук

Число ПЛАНКОВСКИХ Объёмов n3=10186 (то есть, до 10200)
Число планковских Объёмов пространства-ВРЕМЕНИ N4=n4= 10248
Или (примерно) 10250 (штук)

: вар.- ФИО
Выписать обратные
Найти корни


корни
Взаимно обратные элементы
Взаимно обратные элементы
Взаимно

обратные элементы

Взаимно обратные элементы

Взаимно обратные элементы

Взаимно обратные элементы

Число обратимых элементов описывается функцией Эйлера

2 или 3)
Уравнение приводится к виду:

одной прямой равна 0 (по определению).

Точку касания (по предложению Ньютона),

считают за 2 точки.

Если есть только две точки – третья на бесконечности зовётся 0.

частный случай 3: когда первые две точки совпадают, образуя точку касания.

Ф.И.
Возвести в 1ю большую abc степень k, взаимно простую

с φ(n)

использовав обратный в кольце φ(n) вычислить
И Декодировать сообщение.

29341, 41041, 46657, 52633, 62745, 63973, 75361, …
Кармайкловы числа имеют

по меньшей мере три простых положительных множителя.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             
Первые кармайкловы числа с четырьмя простыми множителями:                                                                                                                                                                                                                                                                                                                                                                                                           

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

псевдопростое

число

кармайкла

Первые числа Кармайкла из 4х чисел

Первые числа Кармайкла

(генерировать на калькуляторе (или в экселе)).

*Провести частотный анализ текста в

Экселе

№ b+a+d (фио)
Обратить по данному модулю число а+b+c+d

общение сВ
- МеткаСообщения

R
Корнями являются
Теорема ВИЕТА

A выбирает с. r
Передаёт его В
* B случайным обр. выбирает
Передаёт

его A

или

* A вычисляет

и передаёт его В

проверка

если

* B проверяет

если

Отвергает без проверки

repeat

until

Алфавит
a 0
b 1
c2
d3
e4
f5
g6
h7
I8
j9
k10
l11
m12
n13
o14
p15
q16
r17
s18
t19
u20
v21
w22
x23
y24
z25
а0
б1
в2
г3
д4
е5
ё6
ж7
з8
ий9
к10
л11
м12
н13
о14
п15
р16
с17
т18
у19
ф20
х21
ц22
ч23
ш24
щ25
ъ26
ы27
ь28
э29
ю30
я31
А0
б1
в2
г3
д4
её5
ж6
з7
ий8
к9
л10
м11
н12
о13
п14
р15
с16
т17
у18
ф19
х20
ц21
ч22
ш23
щ24
ъь25
ы26
э27
ю28
я29
А0
б1
в2
г3
д4
е5
ё6
ж7
з8
и9
й10
к11
л12
м13
н14
о15
п16
р17
с18
т19
у20
ф21
х22
ц23
ч24
ш25
щ26
ъ27
ы28
ь29
э30
ю31
я32
26-ричная
32-ричная
30-ричная
Ф.И.О. инициалы
А1
б2
в3
г4
д5
е6
ё7
ж8
з9
и10
й11
к12
л13
м14
н15
о16
п17
р18
с19
т20
у21
ф22
х23
ц24
ч25
ш26
щ27
ъ28
ы29
ь30
э31
ю32
я33
Ф.И. инициалы
текст
А1
б2
в3
г4
д5
е6
ё7
ж8
з9
и10
й11
к12
л13
м14
н15
о16
п17
р18
с19
т20
у21
ф22
х23
ц24
ч25
ш26
щ27
ъ28
ы29
ь30
э31
ю32
я33

≤ p-1
0≤ ≤ p-1
0≤

≤ p-1

=1

Теорема: существует неприводимый многочлен любой степени n

0≤ ≤ p-1

Многочленов степени n


В точности

неразложим

проверка

откуда

элементы
Указать порядок каждого элемента группы

числа

Зашифровать

II. 101000100 001000101

9 цифр, соответственно
9 действий
III. 1. Если первая

цифра – 1,
то k = a, иначе k = 1
2. 6*6 mod 606 = 36 mod 606 = 36
3. 36*36 mod 606 = 84. т.к. 3-я цифра – 1, k = 1*84 mod 606; k = 84
4. 84*84 mod 606 = 7056 mod 606 = 390
5. 390*390 mod 606 = 152100 mod 606 = 600
6. 600*600 mod 606 = 360000 mod 606 = 36
7. 36*36 mod 606 = 84. т.к. 7-я цифра – 1, k = 84*84 mod 606; k = 390
8. 84*84 mod 606 = 7056 mod 606 = 390
9. 390*390 mod 606 = 600. т.к. 9-я цифра – 1, k = 390*600 mod 606 = 84

Алгоритм быстрого возведения в степень по модулю