Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
(1) Сочетание (объединение) коррелированных переменных. 1 В данном примере мы
Содержание
- 1. (1) Сочетание (объединение) коррелированных переменных. 1 В данном примере мы
- 2. 2Первый метод гласит: если коррелированные переменные одинаковы
- 3. 3Данное действие определенно можно выполнить с помощью
- 4. 4Объединение и подсчет среднего значения этих трех
- 5. (2) Отбрасывание (упущение) одной из коррелированных переменных.5Второй Метод:
- 6. 6Однако, такой подход к решению может быть
- 7. 7Если такое происходит, то метод «упущения» приведет
- 8. 8Третий метод решения проблем с мультиколлинеарностью это
- 9. 9Предположим, что Y это количество потребительских расходов,
- 10. 10Чтобы оперировать данным методом, необходимо использовать временные
- 11. 11Полученные в ходе опроса данные о доходах
- 12. 12Это (простая) линейная регрессия, потому что в
- 13. 13Рассмотрим величину для b2 во
- 14. 14Существует несколько проблем, связанных с данным методом.
- 15. 15Во-вторых, Изначально мы вычисляли предполагаемую единицу
- 16. 16Последний, среди приведенных косвенных методов по улучшению
- 17. 17Данный метод можно объяснить с помощью простой
- 18. 187Значение S увеличивается на 0.09 за каждую
- 19. 19Образование у мамы считается как минимум важнее
- 20. 20Однако соединение показателей ведет к корреляции между
- 21. 21Предположим, что образование (показатели образования) мамы и
- 22. 22Это позволит нам переформировать уравнение, как показано на экране.Возможные косвенные показатели для улучшения мультиколлинеарности.(4) Теоретическое ограничение.
- 23. 23Определяем SP как сумму SM и SF,
- 24. . g SP=SM+SF. reg S ASVABC SP----------------------------------------------------------------------------
- 25. . g SP=SM+SF. reg S ASVABC SP----------------------------------------------------------------------------
- 26. 26Стандартная ошибка SP значительно меньше чем у
- 27. 27Значение t достаточно велико. Это означает, что
- 28. Скачать презентанцию
2Первый метод гласит: если коррелированные переменные одинаковы по своему принципу, то резонно было объединить их в некоторый общий (обобщённый) показатель.Возможные косвенные показатели для улучшения мультиколлинеарности.(1) Сочетание (объединение) коррелированных переменных.
Слайды и текст этой презентации
Слайд 1(1) Сочетание (объединение) коррелированных переменных.
1
В данном примере мы рассмотрим четыре возможных
метода решения проблем с мультиколлинераностью. Первый: Сочетание (Объединение) коррелированных переменных.
косвенные показатели для улучшения мультиколлинеарности.
Слайд 22
Первый метод гласит: если коррелированные переменные одинаковы по своему принципу,
то резонно было объединить их в некоторый общий (обобщённый) показатель.
Возможные
косвенные показатели для улучшения мультиколлинеарности.(1) Сочетание (объединение) коррелированных переменных.
Слайд 33
Данное действие определенно можно выполнить с помощью трех (ASVAB) показателей.
ASVABC считается как среднее значение подсчетов вспомогательных показателей: ASVABAR (арифметически
обоснованный), ASVABWK (группа чисел), and ASVABPC (охват определенной группы чисел).Возможные косвенные показатели для улучшения мультиколлинеарности.
. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 44
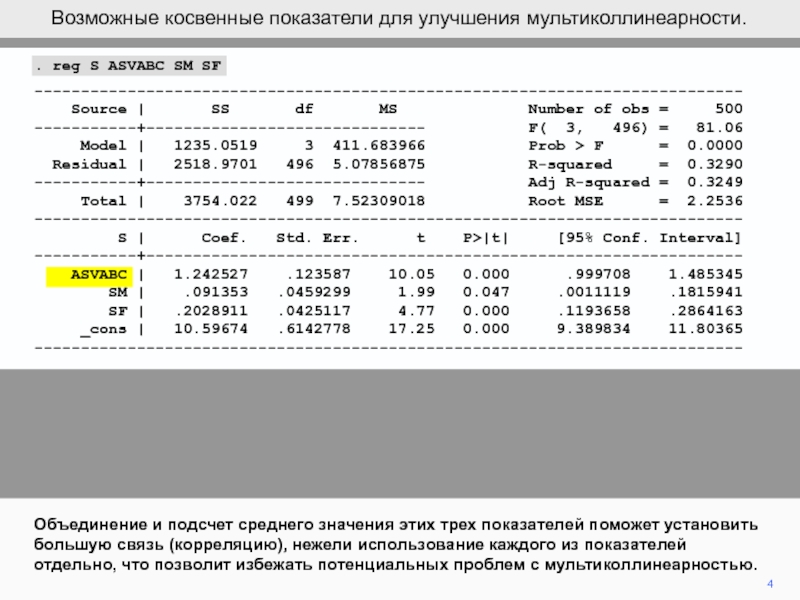
Объединение и подсчет среднего значения этих трех показателей поможет установить
большую связь (корреляцию), нежели использование каждого из показателей отдельно, что
позволит избежать потенциальных проблем с мультиколлинеарностью.Возможные косвенные показатели для улучшения мультиколлинеарности.
. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 5(2) Отбрасывание (упущение) одной из коррелированных переменных.
5
Второй Метод: в случае если
одна из коррелированных переменных имеет незначительный коэффициент, её можно отбросить
(упустить), что также позволит улучшить мультиколлинеарность.Возможные косвенные показатели для улучшения мультиколлинеарности.
Слайд 66
Однако, такой подход к решению может быть опасным. Вполне возможно,
что переменная с незначительным коэффициентом занимает важное место в модели,
а единственная причина, почему её коэффициент незначителен, это проблема в мультиколлинеарности.Возможные косвенные показатели для улучшения мультиколлинеарности.
(2) Отбрасывание (упущение) одной из коррелированных переменных.
Слайд 77
Если такое происходит, то метод «упущения» приведет к неправильным расчетам.
(Подробнее в главе 6)
Возможные косвенные показатели для улучшения мультиколлинеарности.
(2) Отбрасывание (упущение)
одной из коррелированных переменных.
Слайд 88
Третий метод решения проблем с мультиколлинеарностью это использование дополнительной информации
об одной из переменных, если такая информация имеется.
(3) Эмпирическое ограничение на
основе дополнительных данных.Возможные косвенные показатели для улучшения мультиколлинеарности.
Слайд 99
Предположим, что Y это количество потребительских расходов, X это количество
располагаемого личного дохода, а P – ценовой индекс.
Возможные косвенные показатели
для улучшения мультиколлинеарности.(3) Эмпирическое ограничение на основе дополнительных данных.
Слайд 1010
Чтобы оперировать данным методом, необходимо использовать временные ряды. Если показатели
X и P являются значимыми (максимально коррелированы), что является частым
случаем при использовании временных рядов, то проблема с мультиколлинеарностью может быть устранена данным методом.Возможные косвенные показатели для улучшения мультиколлинеарности.
(3) Эмпирическое ограничение на основе дополнительных данных.
Слайд 1111
Полученные в ходе опроса данные о доходах и расходах. Регрессия
Y’ от X'. (отметка ‘ с буквенными обозначениями переменных, показывает,
что это данные, полученные в ходе опроса, а не данные уравнения.)Возможные косвенные показатели для улучшения мультиколлинеарности.
(3) Эмпирическое ограничение на основе дополнительных данных.
Слайд 1212
Это (простая) линейная регрессия, потому что в ходе опроса был
выявлен сравнительно маленький разброс цены, которую уплачивали опрашиваемые.
Возможные косвенные показатели
для улучшения мультиколлинеарности.(3) Эмпирическое ограничение на основе дополнительных данных.
Слайд 1313
Рассмотрим величину для b2 во временных рядах. Сократим
X с обеих сторон, и создадим регрессию Z
= Y – X для цены. Это (простая) линейная регрессия, следовательно проблема с мультиколлинеарностью решена.Возможные косвенные показатели для улучшения мультиколлинеарности.
(3) Эмпирическое ограничение на основе дополнительных данных.
Слайд 1414
Существует несколько проблем, связанных с данным методом. Во-первых, коэффициент b2
во временных рядах, может отличаться от самого себя в выборке,
относящейся к одному моменту времени.Возможные косвенные показатели для улучшения мультиколлинеарности.
(3) Эмпирическое ограничение на основе дополнительных данных.
Слайд 1515
Во-вторых, Изначально мы вычисляли предполагаемую единицу X, а
не исконно верную b 2X. При построении Z, мы, через
Y нашли погрешность измерения зависимой переменной.Возможные косвенные показатели для улучшения мультиколлинеарности.
(3) Эмпирическое ограничение на основе дополнительных данных.
Слайд 1616
Последний, среди приведенных косвенных методов по улучшению мультиколлинеарности, это метод
теоретического сокращения, который определяется как гипотетическое соотношение между параметрами регрессионной
модели.(4) Теоретическое ограничение.
Возможные косвенные показатели для улучшения мультиколлинеарности.
Слайд 1717
Данный метод можно объяснить с помощью простой модели на примере
сверху. Предположим, что значение переменной S, Зависит от ASVABC, а
само значение S построено с помощью определенных данных о маме и папе, SM и SF, соответственно.Возможные косвенные показатели для улучшения мультиколлинеарности.
(4) Теоретическое ограничение.
Слайд 18187
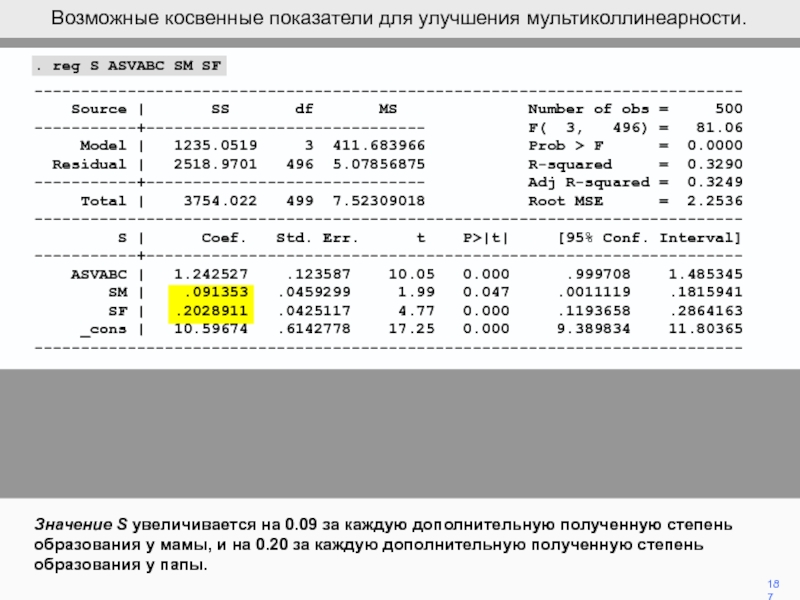
Значение S увеличивается на 0.09 за каждую дополнительную полученную степень
образования у мамы, и на 0.20 за каждую дополнительную полученную
степень образования у папы.Возможные косвенные показатели для улучшения мультиколлинеарности.
. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 1919
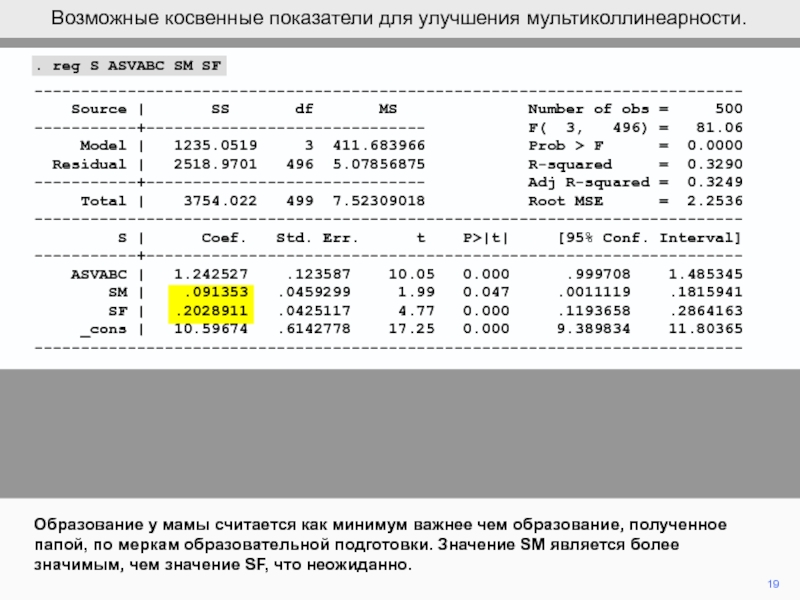
Образование у мамы считается как минимум важнее чем образование, полученное
папой, по меркам образовательной подготовки. Значение SM является более значимым,
чем значение SF, что неожиданно.Возможные косвенные показатели для улучшения мультиколлинеарности.
. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 2020
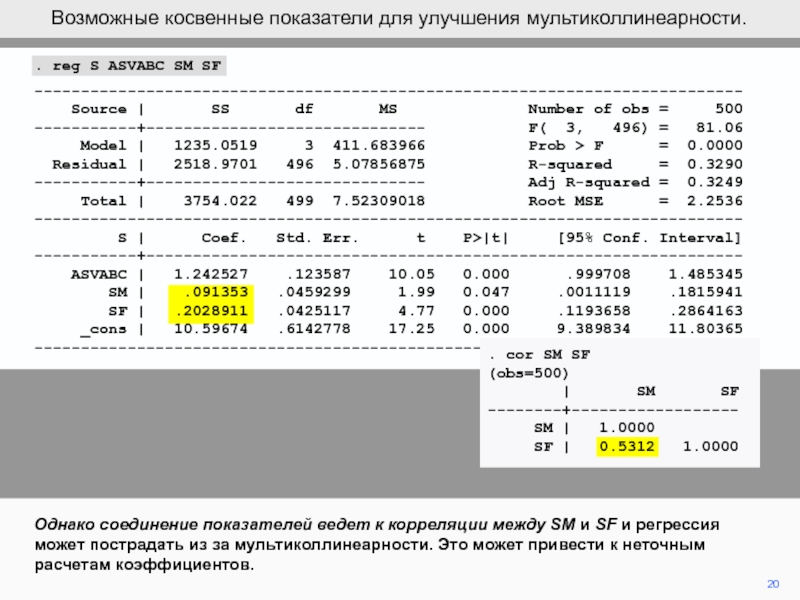
Однако соединение показателей ведет к корреляции между SM и SF
и регрессия может пострадать из за мультиколлинеарности. Это может привести
к неточным расчетам коэффициентов.Возможные косвенные показатели для улучшения мультиколлинеарности.
. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
. cor SM SF
(obs=500)
| SM SF
--------+------------------
SM | 1.0000
SF | 0.5312 1.0000
Слайд 2121
Предположим, что образование (показатели образования) мамы и папы одинаково важны,
в таком случае мы можем наложить ограничениеb3 = b4.
Возможные
косвенные показатели для улучшения мультиколлинеарности.(4) Теоретическое ограничение.
Слайд 2222
Это позволит нам переформировать уравнение, как показано на экране.
Возможные косвенные
показатели для улучшения мультиколлинеарности.
(4) Теоретическое ограничение.
Слайд 2323
Определяем SP как сумму SM и SF, переформировываем уравнение, как
показано на экране. Проблема, вызванная корреляцией между SM и SF,
была устранена.Возможные косвенные показатели для улучшения мультиколлинеарности.
(4) Теоретическое ограничение.
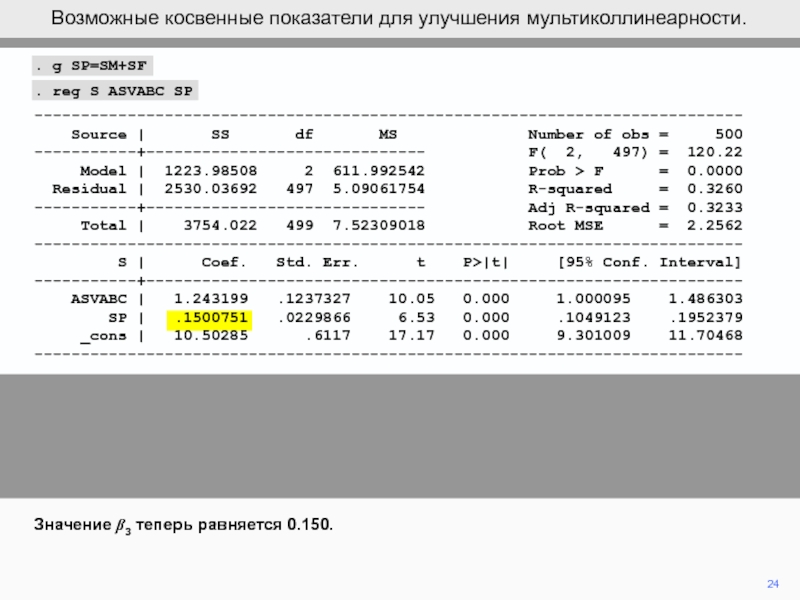
Слайд 24. g SP=SM+SF
. reg S ASVABC SP
----------------------------------------------------------------------------
Source |
SS df
MS Number of obs = 500-----------+------------------------------ F( 2, 497) = 120.22
Model | 1223.98508 2 611.992542 Prob > F = 0.0000
Residual | 2530.03692 497 5.09061754 R-squared = 0.3260
-----------+------------------------------ Adj R-squared = 0.3233
Total | 3754.022 499 7.52309018 Root MSE = 2.2562
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.243199 .1237327 10.05 0.000 1.000095 1.486303
SP | .1500751 .0229866 6.53 0.000 .1049123 .1952379
_cons | 10.50285 .6117 17.17 0.000 9.301009 11.70468
----------------------------------------------------------------------------
24
Значение b3 теперь равняется 0.150.
Возможные косвенные показатели для улучшения мультиколлинеарности.
Слайд 25. g SP=SM+SF
. reg S ASVABC SP
----------------------------------------------------------------------------
S | Coef. Std. Err.
t P>|t| [95% Conf. Interval]-----------+----------------------------------------------------------------
ASVABC | 1.243199 .1237327 10.05 0.000 1.000095 1.486303
SP | .1500751 .0229866 6.53 0.000 .1049123 .1952379
_cons | 10.50285 .6117 17.17 0.000 9.301009 11.70468
----------------------------------------------------------------------------
25
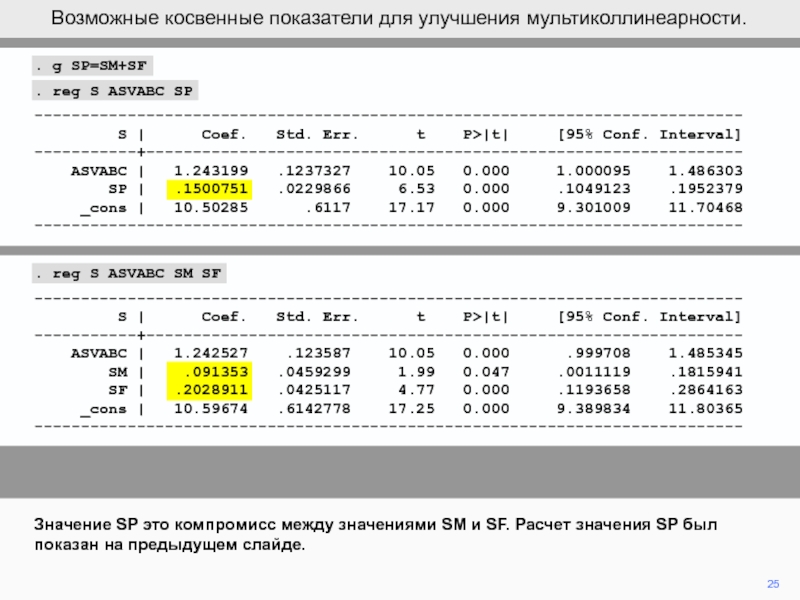
Возможные косвенные показатели для улучшения мультиколлинеарности.
Значение SP это компромисс между значениями SM и SF. Расчет значения SP был показан на предыдущем слайде.
. reg S ASVABC SM SF
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 2626
Стандартная ошибка SP значительно меньше чем у SM и SF.
Использование ограничения привело нас к увеличению эффективности решения задачи, что
помогло решить и проблему с мультиколлинеарностью.Возможные косвенные показатели для улучшения мультиколлинеарности.
. g SP=SM+SF
. reg S ASVABC SP
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.243199 .1237327 10.05 0.000 1.000095 1.486303
SP | .1500751 .0229866 6.53 0.000 .1049123 .1952379
_cons | 10.50285 .6117 17.17 0.000 9.301009 11.70468
----------------------------------------------------------------------------
. reg S ASVABC SM SF
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 2727
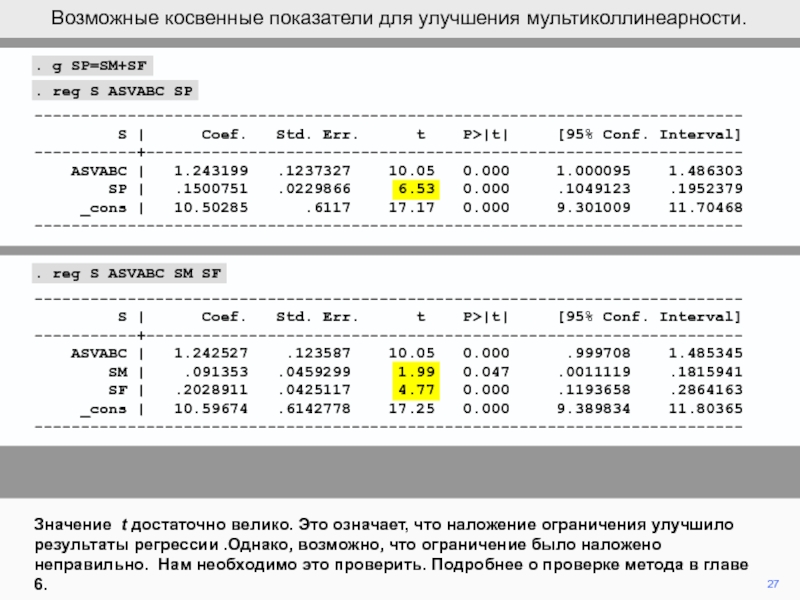
Значение t достаточно велико. Это означает, что наложение ограничения улучшило
результаты регрессии .Однако, возможно, что ограничение было наложено неправильно. Нам
необходимо это проверить. Подробнее о проверке метода в главе 6.Возможные косвенные показатели для улучшения мультиколлинеарности.
. g SP=SM+SF
. reg S ASVABC SP
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.243199 .1237327 10.05 0.000 1.000095 1.486303
SP | .1500751 .0229866 6.53 0.000 .1049123 .1952379
_cons | 10.50285 .6117 17.17 0.000 9.301009 11.70468
----------------------------------------------------------------------------
. reg S ASVABC SM SF
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
