Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной к исследованию функций и построению графиков
Содержание
- 1. Применение производной к исследованию функций и построению графиков
- 2. научиться применять таблицу производных при исследовании функций и построении графиковЦель урока:
- 3. Вариант 1.(Cu)’=……=(u’v-v’u)/v²(cos x)’=……=1/cos² x(ex)’=…Вариант 2.C’=……=(u’v+v’u)(sin x)’=……=-1/sin² x(xn)’=…Вариант
- 4. Одной из основных задач, возникающих при исследовании
- 5. Функция y=f(x) называется возрастающей в некотором интервале,
- 6. возрастающаяубывающаяубывающаяубывающаявозрастающаявозрастающая и убывающая на интервалахвозрастающая и убывающая на интервалахвозрастающая и убывающая на интервалах
- 7. Если дифференцируемая функция y=f(x) возрастает (убывает) в
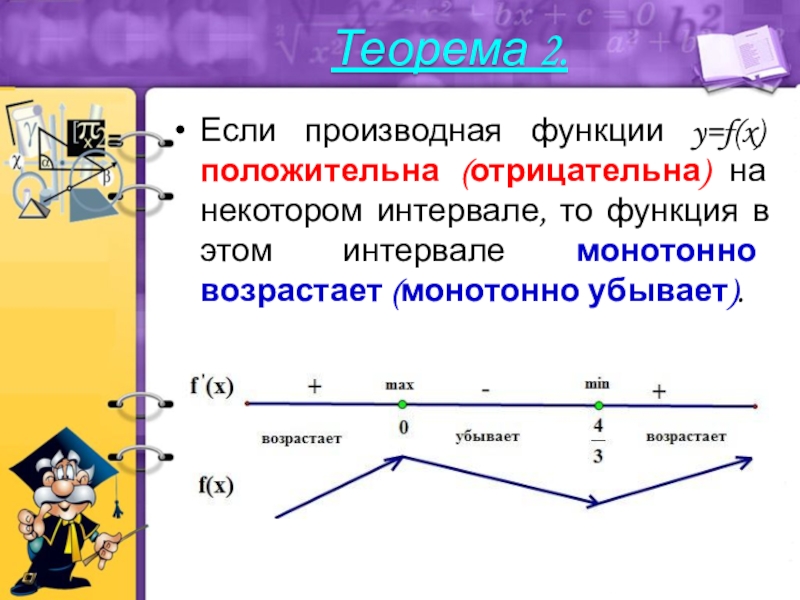
- 8. Если производная функции y=f(x) положительна (отрицательна) на
- 9. Находим область определения функции f(x).Вычисляем производную f’(x)
- 10. Область определения: R. Функция непрерывна.Вычисляем производную :
- 11. Область определения: R. Функция непрерывна.Вычисляем производную :
- 12. Точку x=x0 называют точкой минимума функции y=f(x),
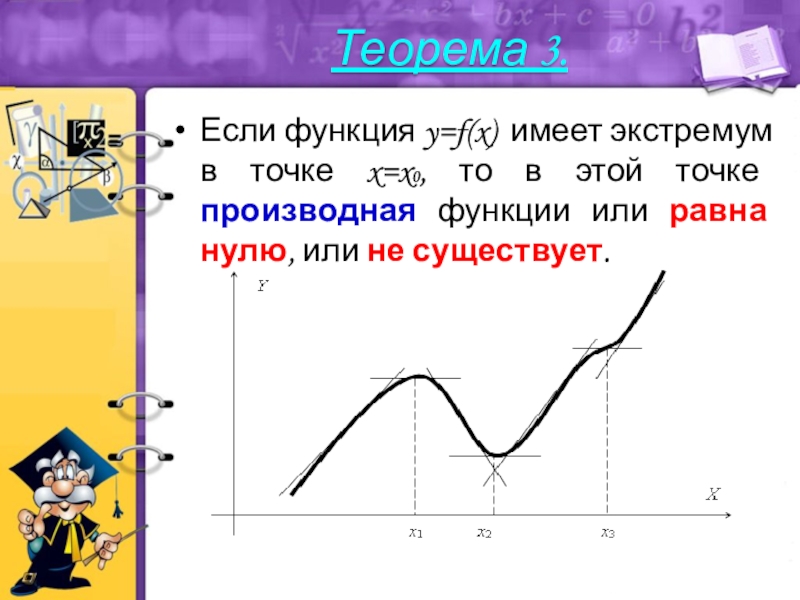
- 13. Если функция y=f(x) имеет экстремум в точке
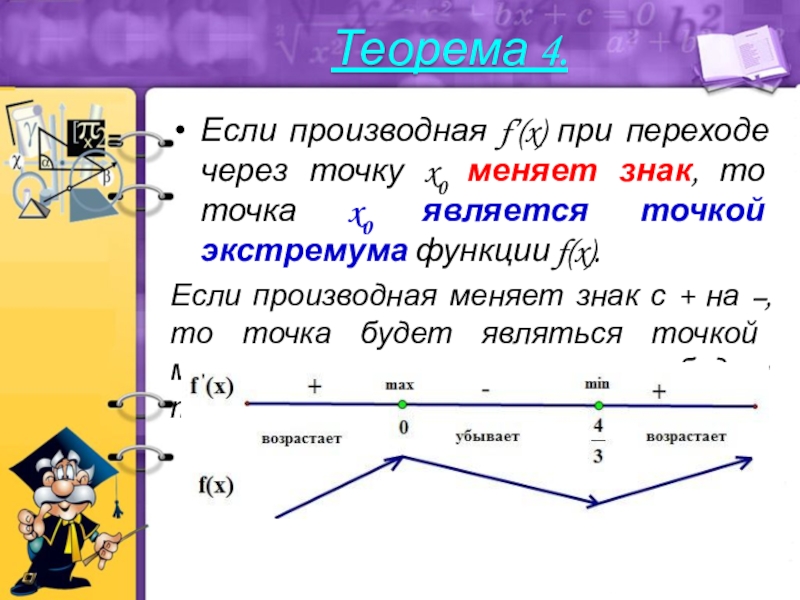
- 14. Если производная f’(x) при переходе через точку
- 15. Область определения: R. Функция непрерывна.Вычисляем производную :
- 16. Определение возрастающей (убывающей) функции.Теорема о возрастании (убывании)
- 17. Работа на уроке:Задание на дом:
- 18. Удачи!
- 19. Скачать презентанцию
научиться применять таблицу производных при исследовании функций и построении графиковЦель урока:
Слайды и текст этой презентации
Слайд 2научиться применять таблицу производных при исследовании функций и построении графиков
Цель
урока:
Слайд 3Вариант 1.
(Cu)’=…
…=(u’v-v’u)/v²
(cos x)’=…
…=1/cos² x
(ex)’=…
Вариант 2.
C’=…
…=(u’v+v’u)
(sin x)’=…
…=-1/sin² x
(xn)’=…
Вариант 1.
(Cu)’=Cu’
(u/v)=(u’v-v’u)/v²
(cos x)’=-sin x
tg
x=1/cos² x
(ex)’=ex
Вариант 2.
C’=0
(uv)’=(u’v+v’u)
(sin x)’=cos x
ctg x=-1/sin² x
(xn)’=n*xn-1
Математический диктант:
Слайд 4Одной из основных задач, возникающих при исследовании функции, является нахождение
промежутков монотонности функции (промежутков возрастания и убывания). Такой анализ легко
сделать с помощью производной.Классная работа
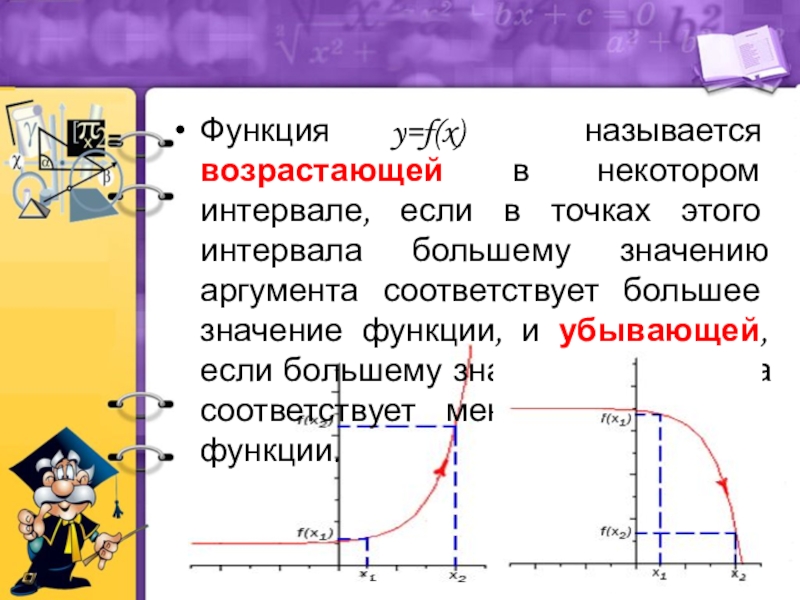
Слайд 5Функция y=f(x) называется возрастающей в некотором интервале, если в точках
этого интервала большему значению аргумента соответствует большее значение функции, и
убывающей, если большему значению аргумента соответствует меньшее значение функции.
Слайд 6возрастающая
убывающая
убывающая
убывающая
возрастающая
возрастающая и убывающая
на интервалах
возрастающая и убывающая
на интервалах
возрастающая и
убывающая
на интервалах
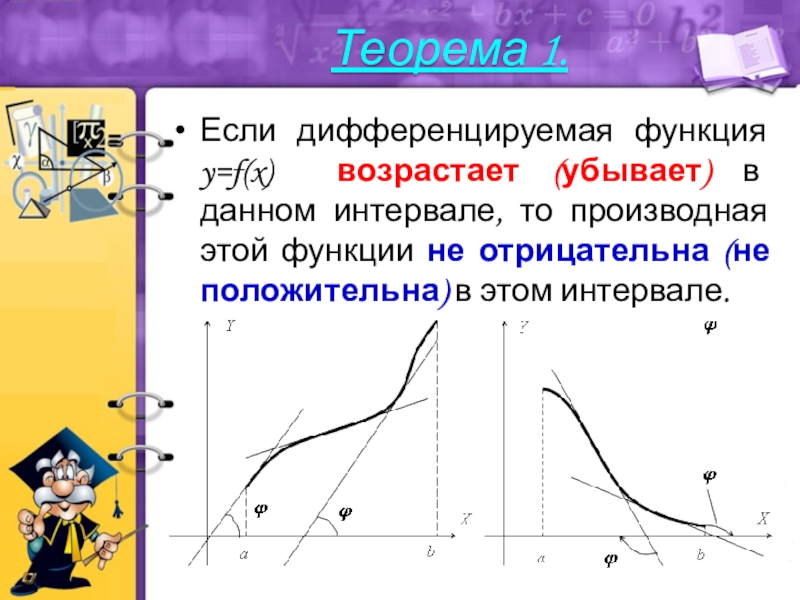
Слайд 7Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то
производная этой функции не отрицательна (не положительна) в этом интервале.
Теорема
1.
Слайд 8Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то
функция в этом интервале монотонно возрастает (монотонно убывает).
Теорема 2.
Слайд 9Находим область определения функции f(x).
Вычисляем производную f’(x) данной функции.
Находим точки,
в которых f’(x)=0 или не существует. Эти точки называются критическими
для функции f(x).Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.
Правило нахождения интервалов монотонности
Слайд 10Область определения: R. Функция непрерывна.
Вычисляем производную : y’=6x²-6x-36.
Находим критические точки:
y’=0.
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;-2]υ[3;+∞),
функция убывает при xϵ[-2;3]. Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5
+
+
-
-2
3
Слайд 11Область определения: R. Функция непрерывна.
Вычисляем производную : y’=3x²-6x.
Находим критические точки:
y’=0.
x²-2x=0
x(x-2)=0
x1=0 и x2=2
Делим область определения на интервалы:
Функция возрастает
при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2]. Пример №2. Найти промежутки монотонности функции y=x³-3x²
-
-
+
0
2
Слайд 12Точку x=x0 называют точкой минимума функции y=f(x), если у этой
точки существует окрестность, для всех точек которой выполняется неравенство f(x)≥f(x0).
Точку
x=x0 называют точкой максимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x0).
Слайд 13Если функция y=f(x) имеет экстремум в точке x=x0, то в
этой точке производная функции или равна нулю, или не существует.
Теорема
3.
Слайд 14Если производная f’(x) при переходе через точку x0 меняет знак,
то точка x0 является точкой экстремума функции f(x).
Если производная меняет
знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимумаТеорема 4.
Слайд 15Область определения: R. Функция непрерывна.
Вычисляем производную : y’=-6x²-6x+12.
Находим критические точки:
y’=0.
-x²-x+2=0
Д=1-4*(-1)*2=1+8=9
x1=1; x2=-2
Делим область определения на интервалы:
x=-2 – точка
минимума. Найдём минимум функции ymin=-24. x=1 – точка максимума. Найдём максимум функции: ymax=3. Пример №3. Найти экстремумы функции
y=-2x³-3x²+12x-4
-
-
+
-2
1
Слайд 16Определение возрастающей (убывающей) функции.
Теорема о возрастании (убывании) функции.
Точка минимума (максимума)
функции.
Стационарные и критические точки производной.
Достаточные условия экстремума функции.
Алгоритм исследования функции
на монотонность и экстремумы.
