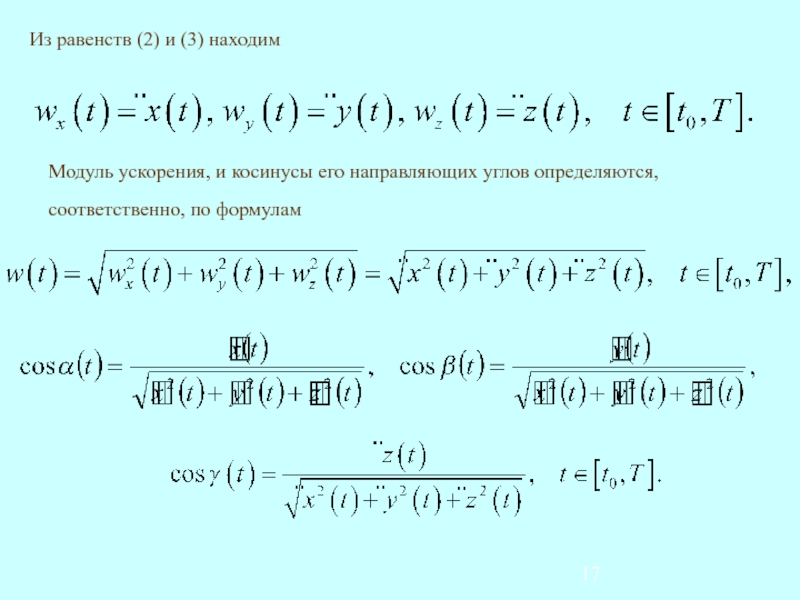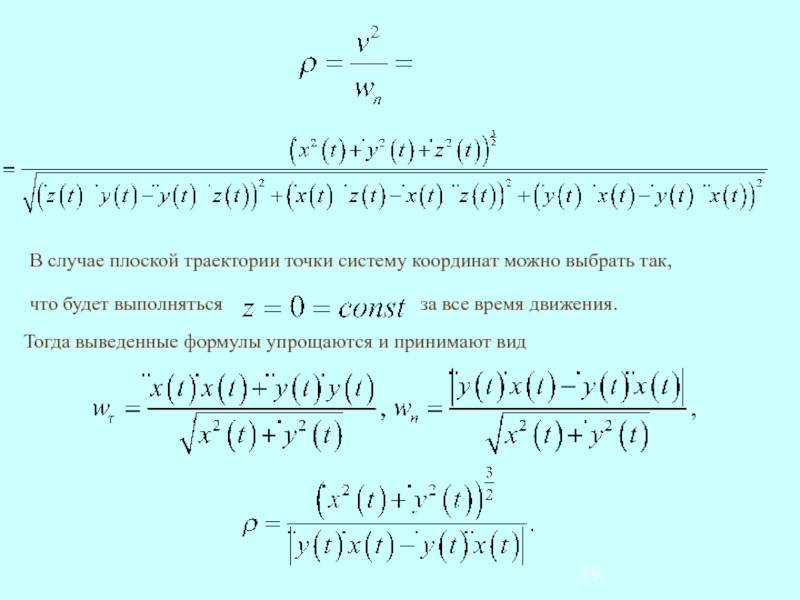ускорения точки при векторном задании движения
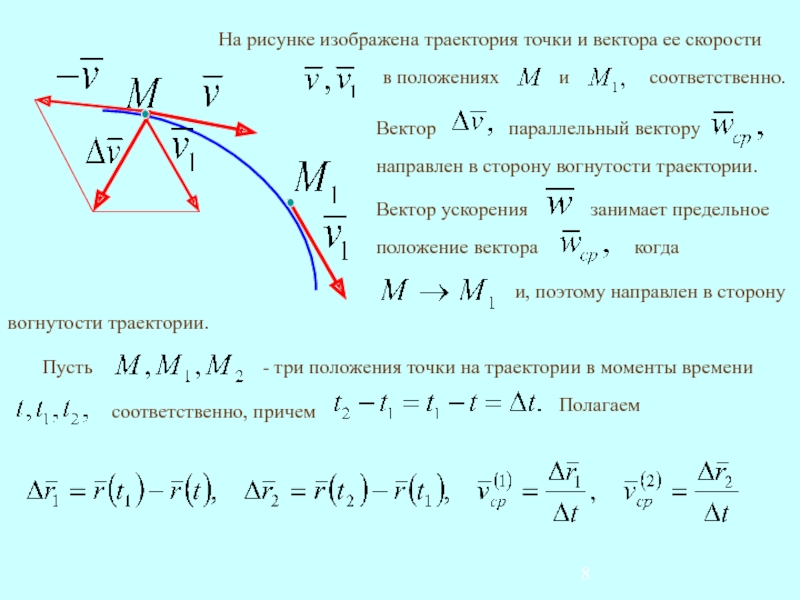
3.3. Разложение вектора ускорения
точки на нормальнуюи касательную составляющие.
3.4. Ускорение точки при естественном способе задания движения.
3.5. Определение ускорения при координатном способе задания движения.
Случай прямоугольных декартовых координат.