1_04.ppt

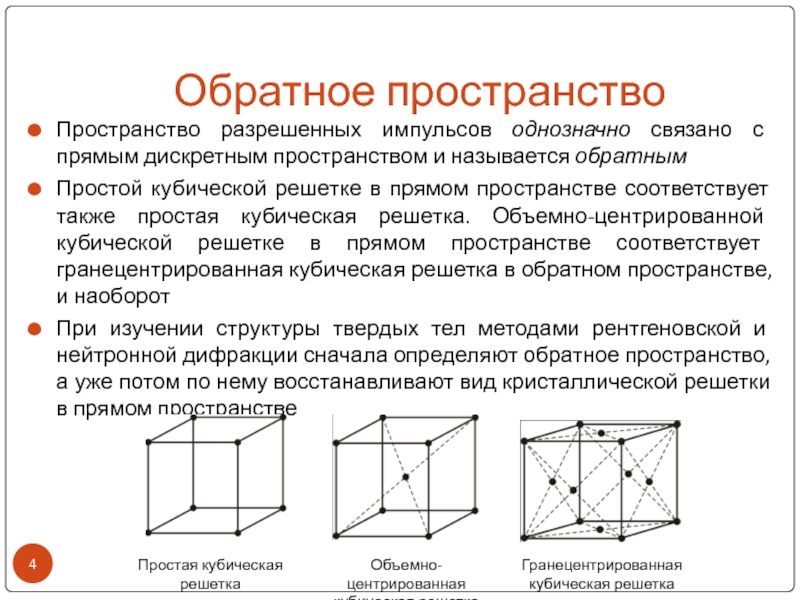
физические величины, определенные в периодическом пространстве кристалла, такие как энергия

электронов и дырок, дисперсия фононных и фотонных возбуждений, волновые функции квазичастиц и др., периодичны в обратном пространстве с периодом обратной решетки
Для конечной дискретной системы обратное пространство также дискретно
Решение уравнения Шредингера для свободной
частицы на периодической решетке –
плоские волны

системе также дискретны, количество неповторяющихся импульсов равно числу узлов; при

увеличении размеров системы соседние значения импульсов все больше приближаются друг к другу:


Все неповторяющиеся импульсы размещены в области

Эта область называется первой зоной Бриллюэна
Часто точку отсчета удобно помещать в центр зоны, тогда первая зона Бриллюэна заключена в интервале

и называется обратным
Простой кубической решетке в прямом пространстве соответствует также

простая кубическая решетка. Объемно-центрированной кубической решетке в прямом пространстве соответствует гранецентрированная кубическая решетка в обратном пространстве, и наоборот
При изучении структуры твердых тел методами рентгеновской и нейтронной дифракции сначала определяют обратное пространство, а уже потом по нему восстанавливают вид кристаллической решетки в прямом пространстве

справедливо:


Теперь задача рассматривается только на одном периоде, разделенном на отрезки

("узлы") длиной 2π/N. Для решения задачи нужно определить коэффициенты Фурье Aq

пределе:

позволяет проводить суммирование в симметричных пределах, что часто бывает удобно
Для

численного расчета всех коэффициентов Фурье в общем случае необходимо порядка N2 операций
Существует алгоритм, который позволяет проводить разложение в ряд Фурье гораздо быстрее – за ~Nlog2N операций – быстрое преобразование Фурье

на два сомножителя:


Подставим в выражение для коэффициентов Фурье:



После преобразований:

необходимо

операций
При известных коэффициентах A(1) количество операций, необходимое для расчета коэффициентов Aq, равно
В общем случае цена для r сомножителей фурье-операций будет

2:


Алгоритм для двоичного разбиения:


Последовательность рекуррентных соотношений для расчета коэффициентов: