lec_3.ppt

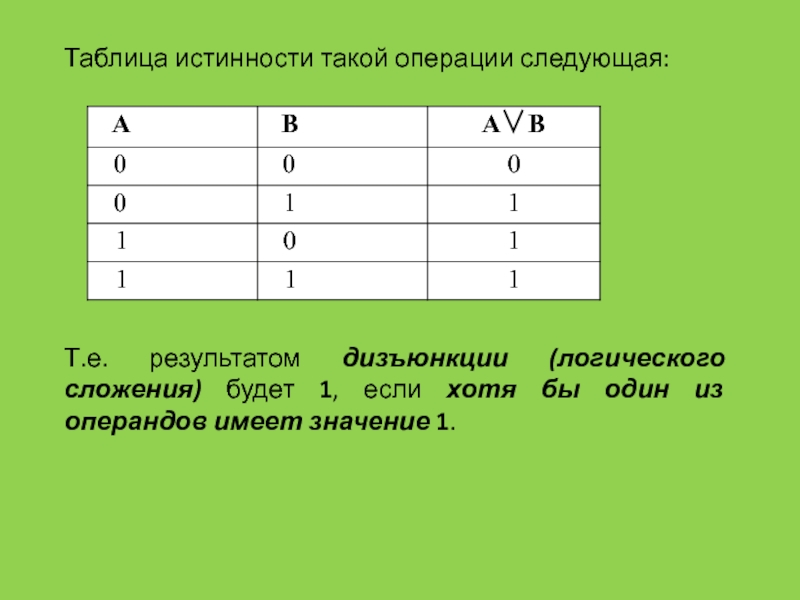
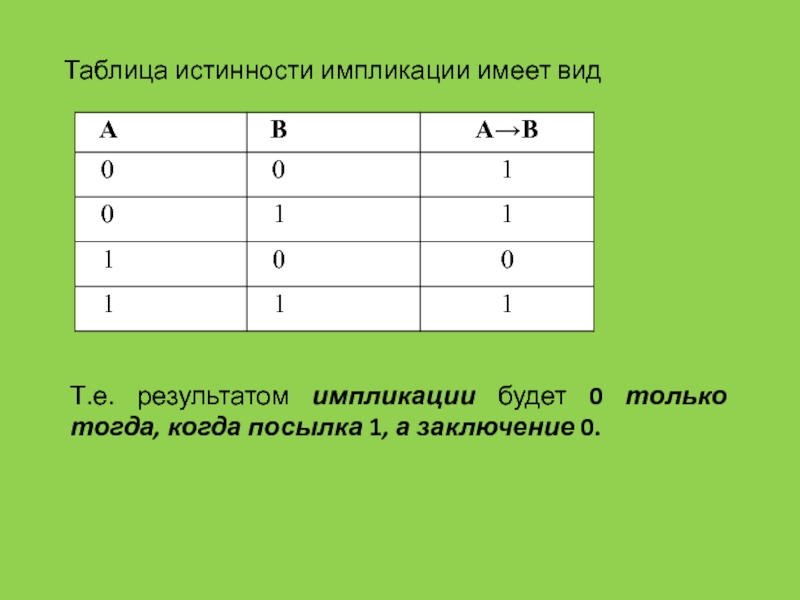
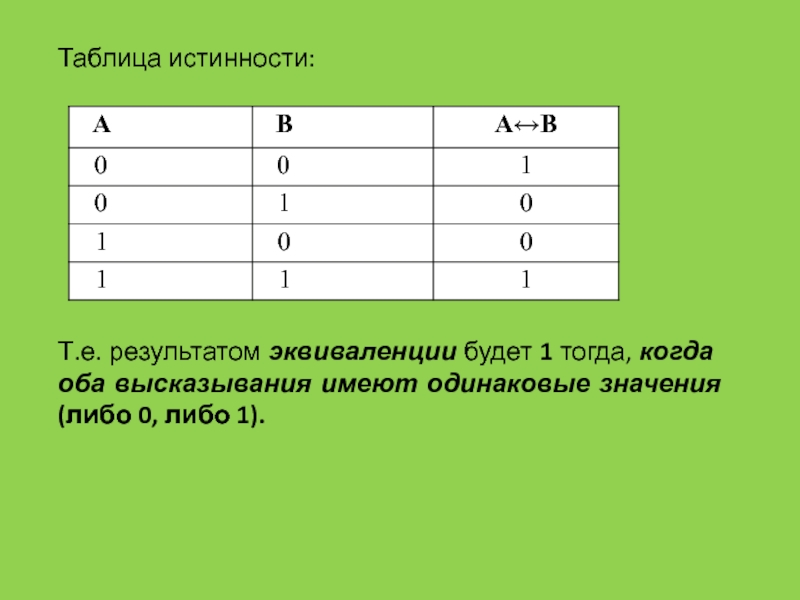
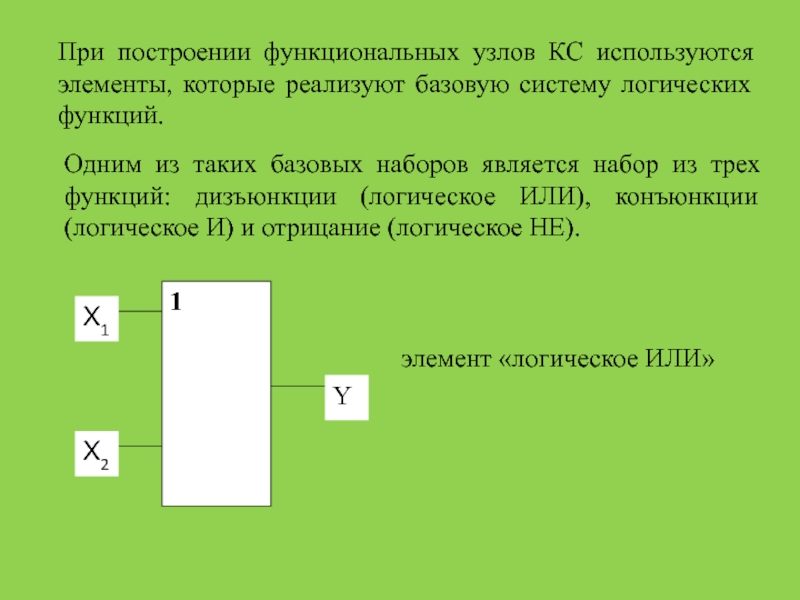
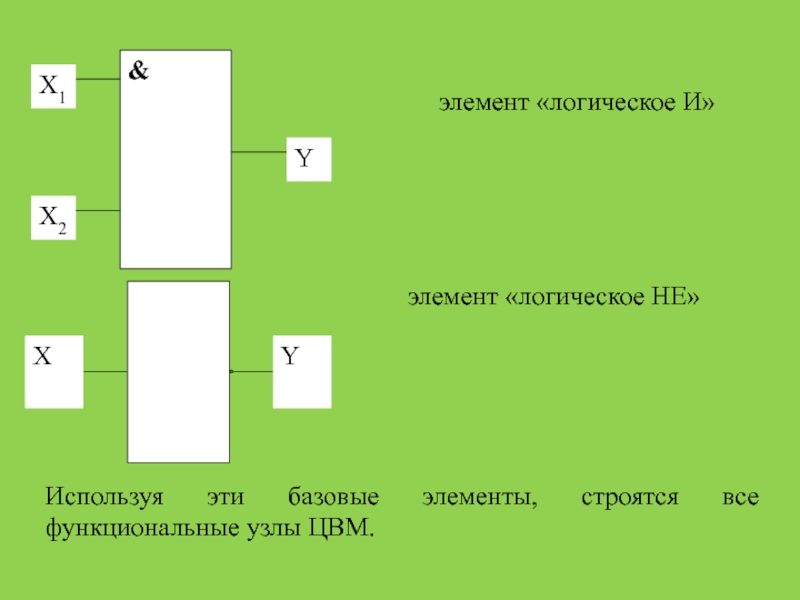
ЭВМ при алгоритмизации и программировании широко используется математический аппарат алгебры

Основное понятие булевой алгебры — высказывание. Высказывания бывают простые и сложные.

Под простым высказыванием понимается повествовательное предложение, в отношении которого имеет смысл утверждение о его истинности или ложности.

Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (значение 0) или ИСТИНА (значение 1).

одинаковые значения истинности, записывается А = В.
Сложное высказывание можно построить

Операцией отрицания А называют высказывание (или –А, или ∀ говорят не А), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно.

Например, если событие А состоит в том, что «завтра экзамен», то «завтра НЕ будет экзамена», истинность одного утверждения автоматически означает ложность второго.

соответствует языковая конструкция, использующая частицу НЕ.
Это правило можно записать в

Такая таблица называется таблицей истинности.

высказывание С, которое истинно только тогда, когда истинны оба высказывания,

Например, пусть высказывание А состоит в том, что «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери», т.е. данная операция применяется, если два высказывания связываются союзом И.

результатом конъюнкции (логического умножения) будет 1 только в том случае,

высказывание С, которое истинно, если истинно хотя бы одно высказывание.

Например, пусть высказывание А состоит в том, что «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе», т.е. данная операция применяется, если два высказывания связываются союзом ИЛИ.

1, если хотя бы один из операндов имеет значение 1.

называется заключением) является новое высказывание С, которое ложно только тогда,

Примером такой операции может быть любое рассуждение типа: если произошло событие А, то произойдет событие В, например, «если идет дождь, то на небе тучи». Очевидно, операция не симметрична, т.е. из В→А не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.

тогда, когда посылка 1, а заключение 0.

которое истинно только тогда, когда оба высказывания имеют одинаковые значения

Примером такой операции может быть любое высказывание типа: событие А равносильно событию В. Например, «идет дождь» равносильно «капает из тучи».

имеют одинаковые значения (либо 0, либо 1).

соглашение о старшинстве операций.
Первыми выполняются операции в скобках, затем операции

систему логических функций.
Одним из таких базовых наборов является набор

элемент «логическое ИЛИ»

функциональные узлы ЦВМ.