Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к консп. лекц_2.ppt
Содержание
- 1. Презентация к консп. лекц_2.ppt
- 2. Введение
- 3. Статистическая грамотность является неотъемлемой составной частью профессиональной
- 4. В настоящее время от работника, занятого в
- 5. Методы экспертных оценок
- 6. МОЗГОВАЯ АТАКАМетоды мозгового штурма или мозговой атаки
- 7. МОЗГОВАЯ АТАКАВо время сеанса мозговой атаки происходит
- 8. Методы мозговой атакиПрямая мозговая атакаОбратная мозговая атакаКомбинированные
- 9. Методы мозговой атакиСинектика (использование аналогий)прямая аналогия –
- 10. Причинно-следственная диаграмма (диаграмма Исикавы)
- 11. Причинно-следственная диаграмма (диаграмма Исикавы) Основная цель
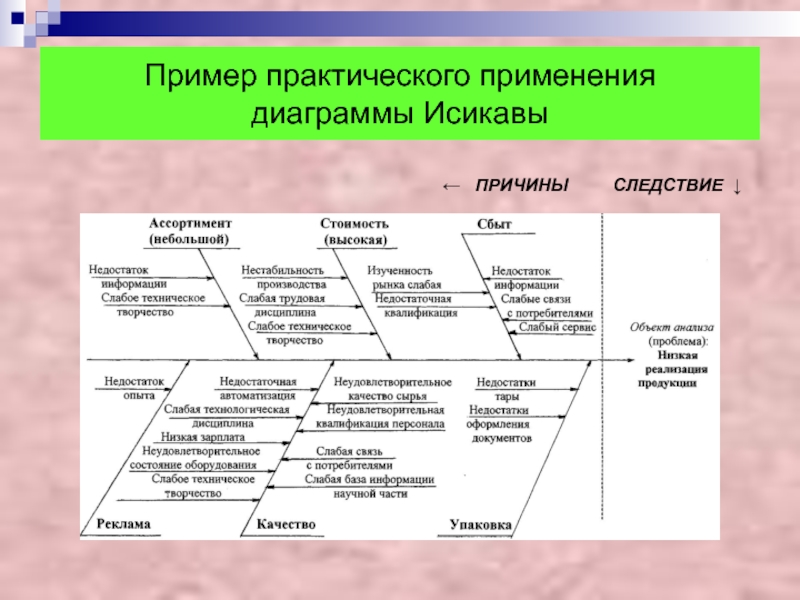
- 12. Пример практического применения диаграммы Исикавы
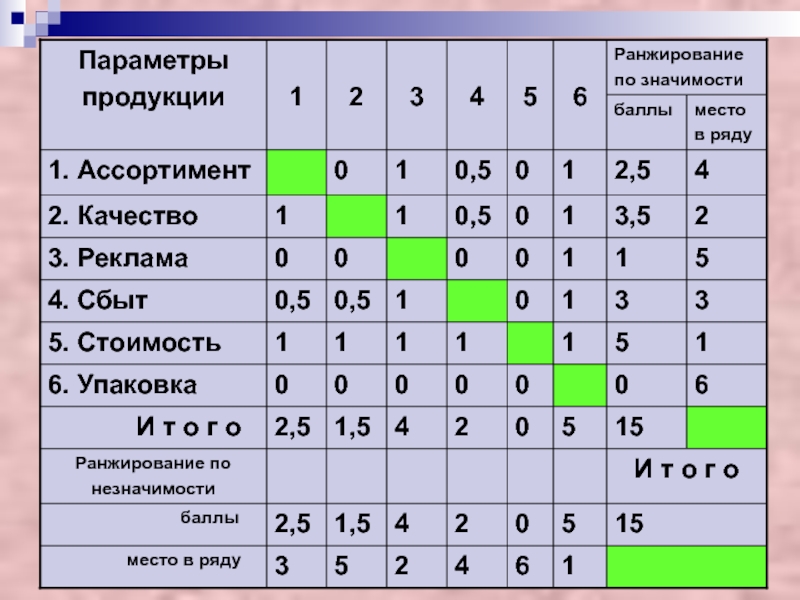
- 13. Ранжирование данныхРанжирование (от фр. ranger - ставить
- 14. Слайд 14
- 15. Диаграмма ПаретоДиаграмма Парето – это графическое изображение
- 16. Диаграмма ПаретоДиаграмма используется для :+ Анализа проблемы
- 17. Формализация априорной информацииМетод ФАИ позволяет получить обобщённую
- 18. Формализация априорной информации
- 19. Формализация априорной информации На практике чаще пользуются
- 20. Формализация априорной информации Коэффициент конкордации изменяется от
- 21. Формализация априорной информации Если имеются «связанные» ранги,
- 22. Методы обработки выборок
- 23. Любая группа однородных данных, собранных
- 24. Б) Характеристики изменчивости (рассеяния) данных в группе:
- 25. Обработка результатов измерений Но часто систематические погрешности
- 26. Обработка результатов измерений Случайные погрешности обусловлены большим
- 27. Обработка результатов измеренийВ вышеприведённой формуле: t -
- 28. Обработка результатов измеренийТочность измерения характеризуется отклонением среднего
- 29. Обработка результатов измерений При испытаниях в технике
- 30. Расслоение данныхЭтот приём позволяет какой-либо массив (совокупность)
- 31. Расслоение данныхМожно получить ценную информацию о причинах
- 32. Расслоение данных ► Метод расслоения в чистом
- 33. Сравнение выборок При предварительном анализе данных наблюдений
- 34. Сравнение выборок Сравнивают выборки по их средним
- 35. Сравнение выборок Сравнение среднеарифметических при равных дисперсиях
- 36. Сравнение выборок Сравнение среднеарифметических при неравных дисперсиях
- 37. Гистограммы Если данные из какой либо выборки
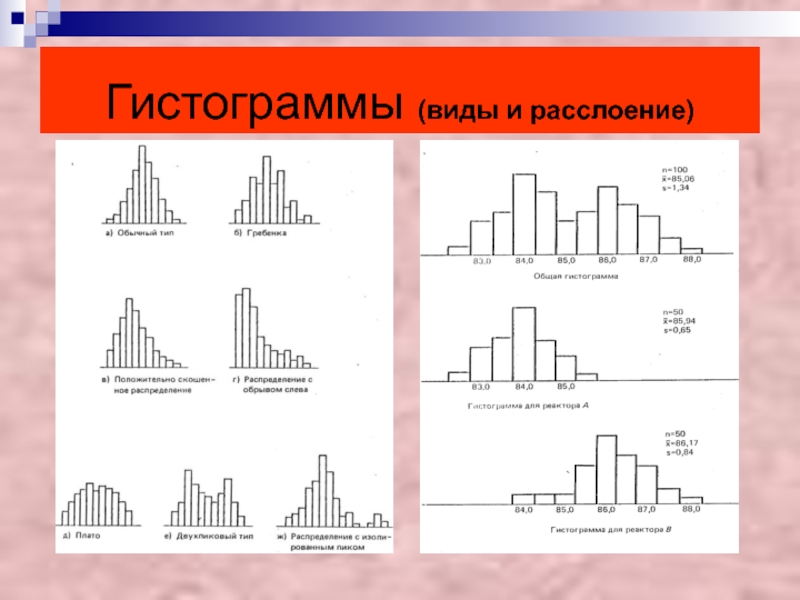
- 38. Гистограммы (виды и расслоение)
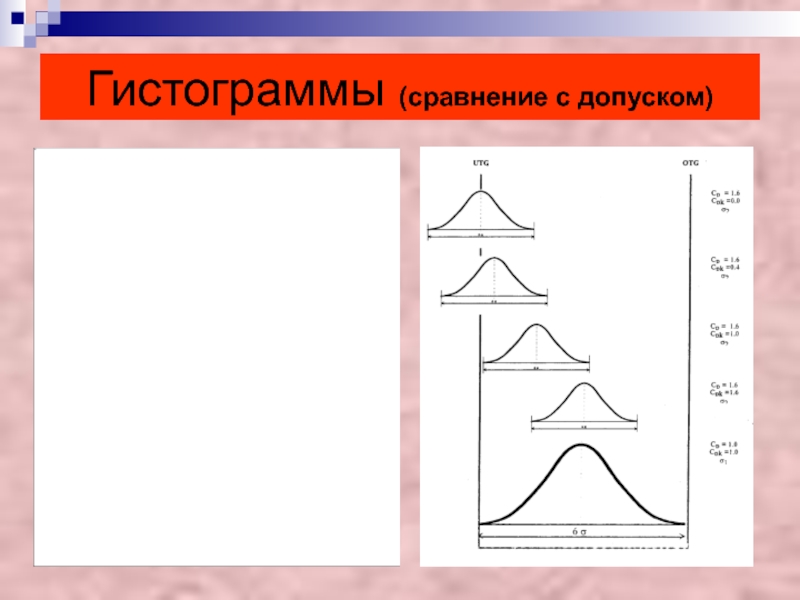
- 39. Гистограммы (сравнение с допуском)
- 40. Гистограммы ► Существует индекс возможностей (или показатель мощности) процесса,
- 41. Гистограммы ► Когда С р (или С
- 42. Временной ряд Этот приём позволяет простейшим способом
- 43. Временной ряд Например, так выглядит временной
- 44. Временной ряд Всякий динамический ряд
- 45. Временной ряд Методы «механического» сглаживания
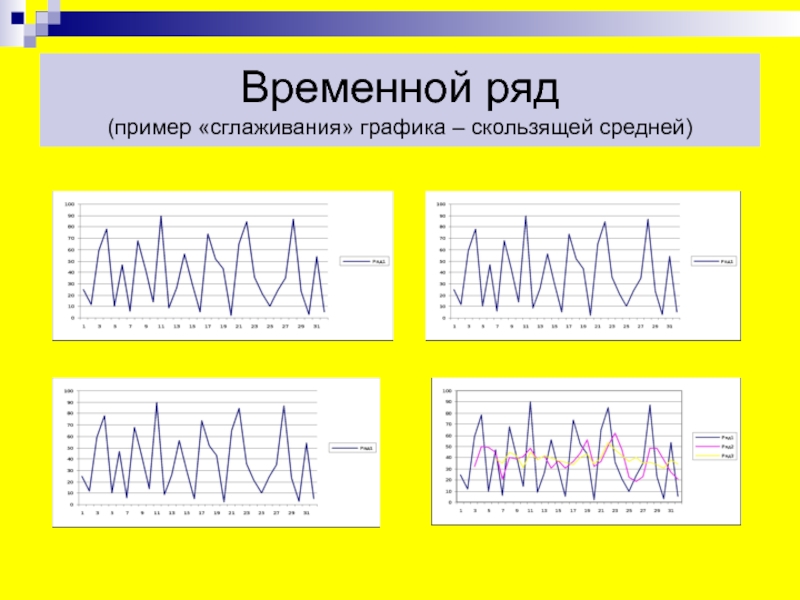
- 46. Временной ряд (пример «сглаживания» графика – скользящей средней)
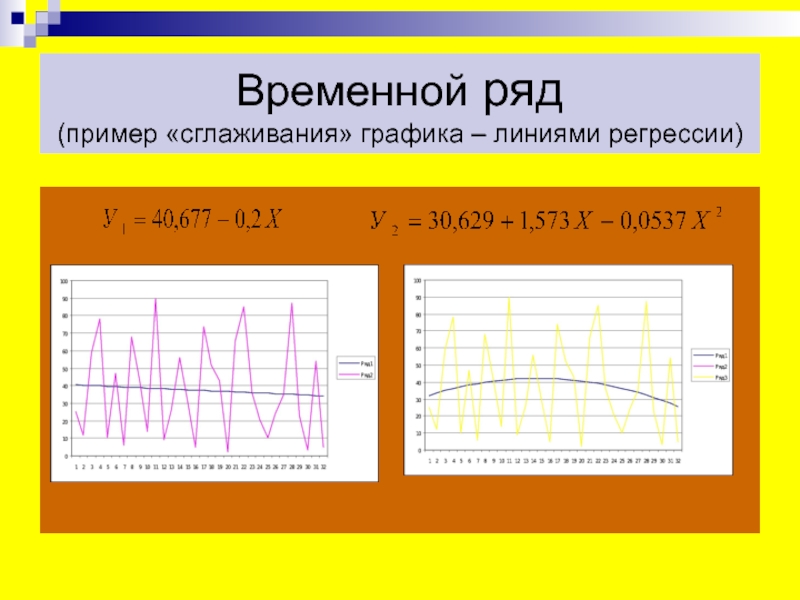
- 47. Временной ряд (пример «сглаживания» графика – линиями регрессии)
- 48. Временной ряд Методы «аналитического» выравнивания Целью
- 49. Контрольные картыДля того, чтобы держать процесс в
- 50. Контрольные карты Контрольная карта представляет собой специальный
- 51. Контрольные картыСтандартом ГОСТ Р 50779.42 (ИСО 8258-91)
- 52. Управление технологическим процессом Для управления процессами используют
- 53. Управление технологическим процессомСреднее процесса неуправляемо – неуправляем процесс
- 54. Управление технологическим процессомВариабельность процесса неуправляема – неуправляем процесс
- 55. Управление технологическим процессомНеуправляемы как среднее, так и вариация процесса – неуправляем процесс
- 56. Управление технологическим процессомУправляемы и среднее, и вариация процесса – управляем процесс
- 57. Корреляционно – регрессионный анализ
- 58. Диаграммы рассеянияДиаграмма разброса, также как и метод
- 59. Диаграммы рассеяния
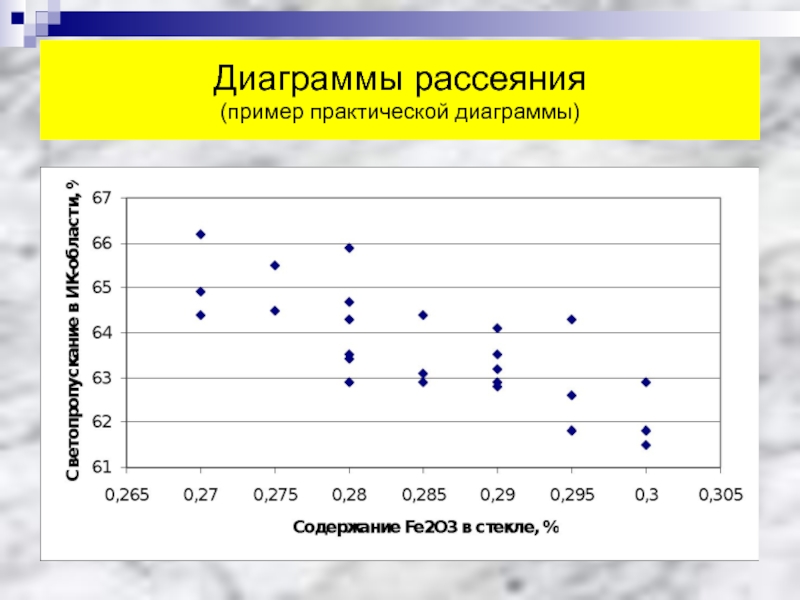
- 60. Диаграммы рассеяния (пример практической диаграммы)
- 61. Корреляция Оценивают степень тесноты (значимость) корреляционной зависимости
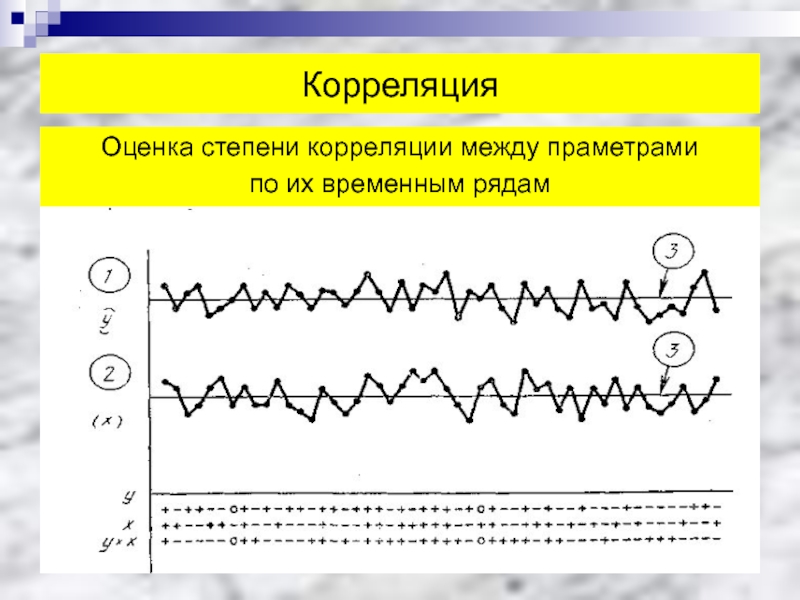
- 62. Корреляция Оценка степени корреляции между праметрами по их временным рядам
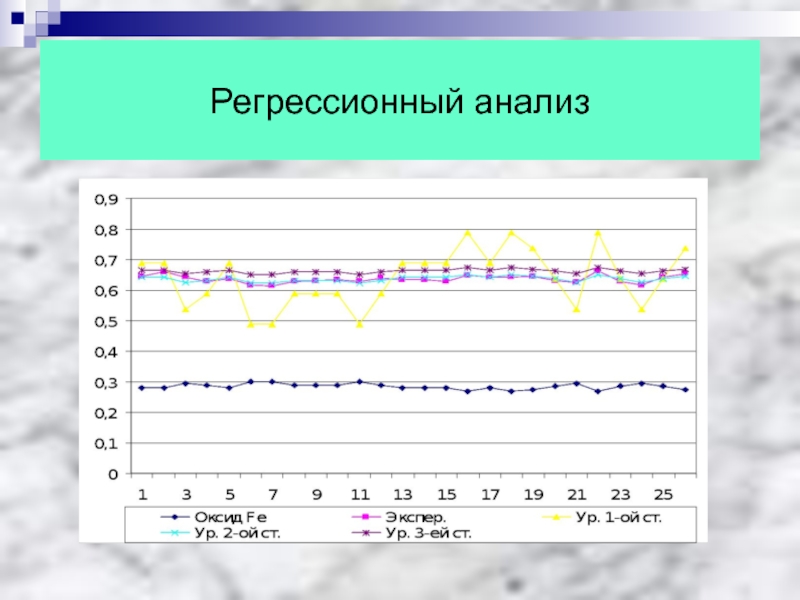
- 63. Регрессионный анализЕсли корреляционный анализ на основе диаграмм
- 64. Регрессионный анализНайти линию регрессии, наиболее адекватно отражающую
- 65. Регрессионный анализНачинают анализ с самой простой формы
- 66. Регрессионный анализРешение системыуравненийметодом вычитанияуравненияС помощьюпрограммы SolverПосле решения
- 67. Регрессионный анализ Теперь необходимо оценить, насколько полученное
- 68. Регрессионный анализОдно из правил оценки адекватности линий
- 69. Регрессионный анализ Как и следовало ожидать, судя
- 70. Регрессионный анализD = 0.916211 – 0.976872 F
- 71. Регрессионный анализ
- 72. Заключение
- 73. Для управления качеством продукции на производстве специалисты
- 74. Ф С АВ экономическом анализе также возникали
- 75. Ф С АВ промышленно развитых странах предприятиями,
- 76. F M E AПрименение метода FMEA обусловлено
- 77. F M E AВ книге «Оценка риска
- 78. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3
Статистическая грамотность является неотъемлемой составной частью профессиональной подготовки каждого специалиста,
имеющего дело с анализом массовых явлений, будь то технические, научные,
социально-общественные, экономические и другие. Работа этих групп специалистов неизбежно связана со сбором, разработкой и анализом данных статистического (массового) характера. Нередко им самим приходится проводить статистический анализ различных типов и направленности либо знакомиться с результатами статистического анализа, выполненного другими.Слайд 4
В настоящее время от работника, занятого в любой области науки,
техники, производства, бизнеса и прочее, связанной с изучением массовых явлений,
требуется, чтобы он был, по крайней мере, статистически грамотным человеком. В конечном счете, невозможно успешно специализироваться по многим дисциплинам без усвоения какого-либо статистического курса. Поэтому большое значение имеет знакомство с общими категориями, принципами и методологией статистического анализа.Слайд 6МОЗГОВАЯ АТАКА
Методы мозгового штурма или мозговой атаки (brainstorming) основываются на
следующем психологическом эффекте.
Если взять группу из 5-8 человек и
каждому предложить независимо индивидуально высказать идеи и предложения по решению поставленной технической задачи, то получим в сумме Q идей. Если предложить этой группе коллективно высказывать идеи по той же задаче, то получим К идей. При этом оказывается К > Q .
Слайд 7МОЗГОВАЯ АТАКА
Во время сеанса мозговой атаки происходит как бы цепная
реакция идей, приводящая к интеллектуальному взрыву.
Методы мозговой атаки представляют собой
эмпирически найденные эффективные способы решения творческих задач. Особенность мозговой атаки – универсальность методов и весьма широкая область их применения. С помощью методов мозговой атаки можно рассматривать почти любую проблему или любое затруднение в сфере человеческой деятельности.
Слайд 8Методы мозговой атаки
Прямая мозговая атака
Обратная мозговая атака
Комбинированные методы мозговой атаки
:
* Двойная прямая атака
*
Обратная и прямая атака* Прямая и обратная атака
* Атака с оценкой идей
Слайд 9Методы мозговой атаки
Синектика (использование аналогий)
прямая аналогия – объект сравнивается с
более или менее
аналогичным объектом из других отраслей техники или с
объектом из живойприроды (например, окраска);
личная аналогия – или э м п а т и я – решающий задачу человек
вживается в образ совершенствуемого объекта, пытаясь выяснить возникающие
при этом чувства, ощущения (например, вы белая ворона, которая хочет
окраситься);
символическая аналогия – обобщённая, абстрактная аналогия
(например, для шлифовального круга символическая аналогия – «точная
шероховатость»);
фантастическая аналогия – в задачу вводятся какие-нибудь
фантастические существа или средства, выполняющие то, что требуется по
условиям задачи (шапка-невидимка, сапоги-скороходы и т.д.).
Слайд 11
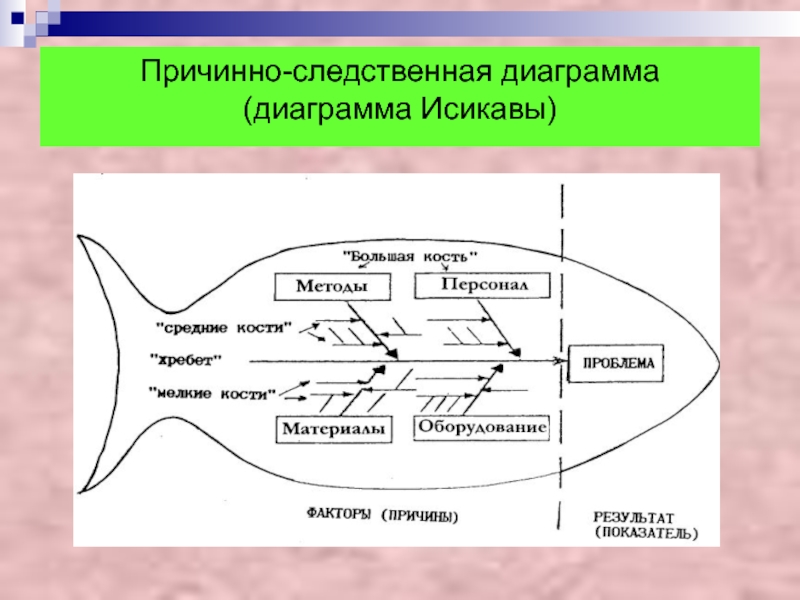
Причинно-следственная диаграмма
(диаграмма Исикавы)
Основная цель составления этой диаграммы выявить как можно
больше причин, влияющих на объект анализа (следствие).
Диаграмма позволяет
выявить и систематизировать различные факторы и условия, оказывающие влияние на рассматриваемую проблему (качество продукции, «узкие места» в технологическом процессе, сложности маркетинга, снижение себестоимости продукции, оценка кадровой ситуации и ещё многое другое). Слайд 13Ранжирование данных
Ранжирование (от фр. ranger - ставить в ряд) -
способ оценки переменной, когда ее значению приписывается место в
последовательности величин (так называемый ранг), определяемое при посредстве порядковой шкалы, часто от большой величины к малой.В методах экспертных оценок ранжирование является основным источником количественной информации, т.е. выполняет такие же фундаментальные методологические функции, как и измерение.
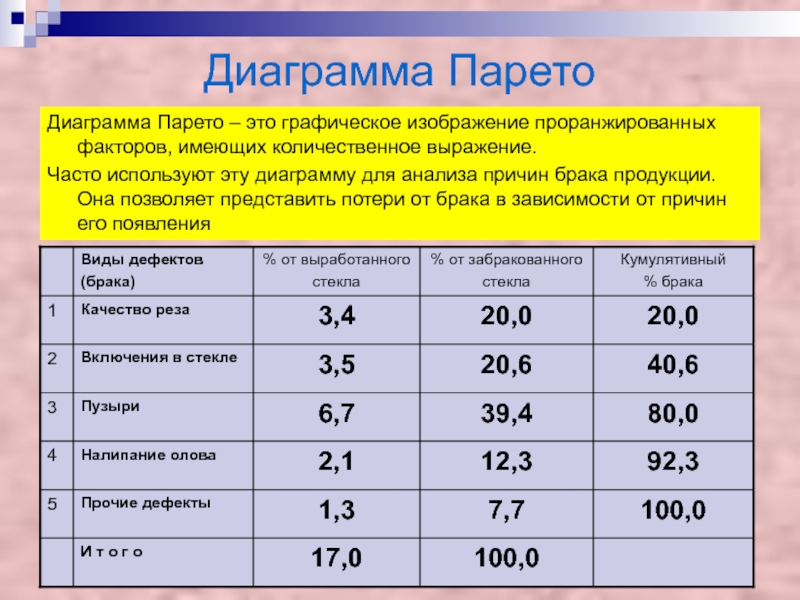
Слайд 15Диаграмма Парето
Диаграмма Парето – это графическое изображение проранжированных факторов, имеющих
количественное выражение.
Часто используют эту диаграмму для анализа причин брака продукции.
Она позволяет представить потери от брака в зависимости от причин его появленияСлайд 16Диаграмма Парето
Диаграмма используется для :
+ Анализа проблемы в поисках новых
перспектив;
+ Сосредоточения внимания на проблемах, упорядоченных по важности;
+ Сопоставления данных
в поисках перемен в различные периоды времени;+ Создания основы для построения кумулятивной линии.
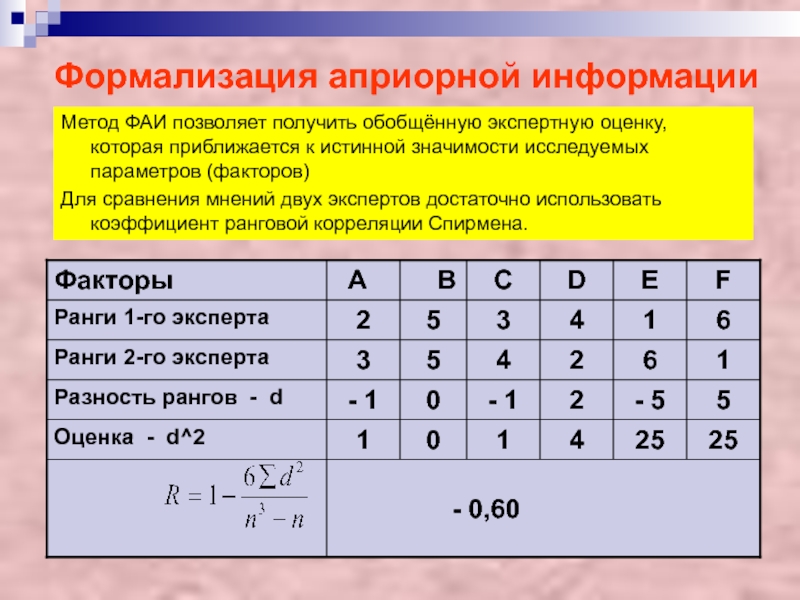
Слайд 17Формализация априорной информации
Метод ФАИ позволяет получить обобщённую экспертную оценку, которая
приближается к истинной значимости исследуемых параметров (факторов)
Для сравнения мнений двух
экспертов достаточно использовать коэффициент ранговой корреляции Спирмена.
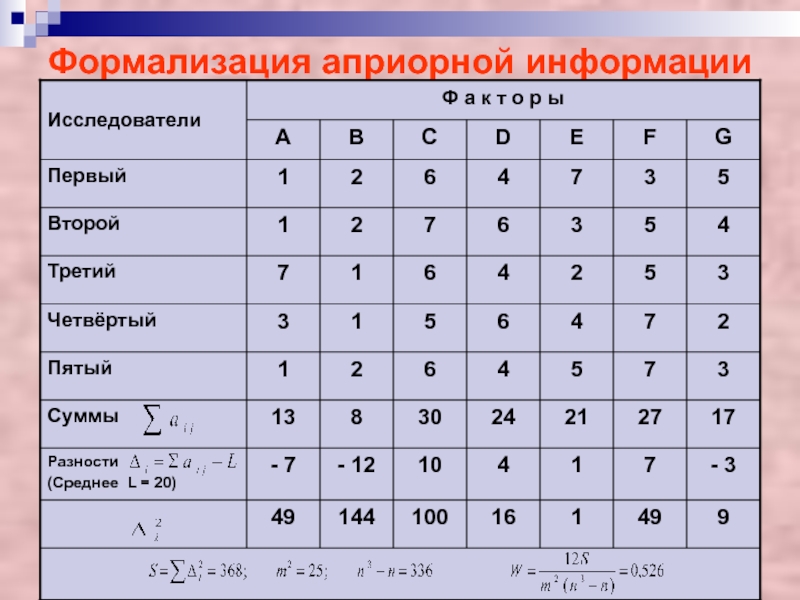
Слайд 19Формализация априорной информации
На практике чаще пользуются не коэффициентами ранговой
корреляции, характеризующими согласованность мнений двух экспертов, а коэффициентом конкордации, определяющим
согласованность мнений группы экспертов:где S – сумма квадратов отклонений (то же, что и Σ d^2 в формуле R ),
m - число экспертов,
n - число ранжируемых факторов.
Слайд 20Формализация априорной информации
Коэффициент конкордации изменяется от 0 до 1.
Чем он больше, тем выше степень согласованности мнений экспертов.
Могут возникать ситуации, когда эксперт не может провести чёткого разграничения между двумя членами ряда. В таком случае вводятся «связанные ранги». Если, например, эксперт не может разграничить третий и четвёртый члены ряда, то обоим членам приписывается дробный номер. Точно также, если нельзя разграничить члены со второго по шестой, то всем им приписывается один и тот же номер 1/5 (2 + 3 + 4 + 5 + 6) = 4.
Слайд 21Формализация априорной информации
Если имеются «связанные» ранги, то коэффициент конкордации
определяется соотношением
где Т i = 1 / 12 Σ (t 3i – t j) , t j – j-е число одинаковых рангов в i-м ранжировании.
Например, если некоторый i-й эксперт указал ранги
1 4,5 4,5 4,5 4,5 8 8 8 10 ,
то для него Т i = 1 / 12 ( 4 3 – 4) + (3 3 – 3 ) = 7.
Суммы Т i подсчитываются для всех тех экспертов, у которых оказались «связанные» ранги.
Слайд 23 Любая группа однородных данных, собранных при измерении параметров
– это статистическая совокупность или более кратко: выборка, т.е. часть
генеральной совокупности.А) Характеристики положения центра группирования данных:
Выборочное среднее арифметическое – это сумма всех данных, делённая на их число:
Мода – это то значение, которое встречается в группе данных наиболее часто. Например, из этого ряда чисел 6, 7, 3, 5, 8, 4, 5, 7, 5
модой будет число £ = 5.
Медиана – это срединное значение данных упорядоченных (или ранжированных) по возрастанию или по убыванию. Например, для этого ряда чисел 2, 2, 3, 3, 5, 7, 7, 8, 8, 8, 9 медианой будет число Ме = 7.
Слайд 24Б) Характеристики изменчивости (рассеяния) данных в группе: Размах: Например, из
ряда чисел 5, 3, 7, 9, 8, 5, 4, 5,
8 R = 9 – 3 = 6 Выборочная дисперсия – σ – равна сумме квадратов отклонений от среднего, делённой на объём выборки: Среднеквадратичное (или стандартное) отклонение – S : Коэффициент вариации – ν :
Слайд 25Обработка результатов измерений
Но часто систематические погрешности не исключают из
результата измерения, а рассчитывают, отдельно их указывая. В качестве границ
неисключённой систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений. В общем случае (при равномерном распределении) неисключаемые систематические погрешности вычисляют по формуле,
где - - граница i-ой неисключённой систематической погрешности; k – коэффициент, определяемой доверительной вероятностью. k =1.1 при P = 0.95 и k = 1.4 при P = 0.99.
Слайд 26Обработка результатов измерений
Случайные погрешности обусловлены большим числом отдельных причин,
не поддающихся точному учёту и действующих в каждом отдельном опыте
различным образом. Случайные ошибки во всех случаях не могут быть исключены из результата измерения. Величину случайных погрешностей определяют принципиальная схема эксперимента, отклонение реальных условий опыта от заданных и, в значительной мере, субъективные особенности экспериментатора. Случайные погрешности подчиняются законам вероятности, в связи с чем многократное повторение одного и того же измерения уменьшает их влияние.Доверительные границы (без учёта знака) случайной погрешности результата измерения рассчитывают [12] по формуле:
Слайд 27Обработка результатов измерений
В вышеприведённой формуле: t - коэффициент Стьюдента, который
в зависимости от доверительной вероятности P и числа результатов наблюдений
n находят по таблице (например, при P = 0.95 если n = 5, то t = 2.571; если n = 16, то t = 2.120; если n = 30, то t = 2.042; при большем числе n, чем 30, независимо от самого числа n коэффициент t= 1.960); величина S () называется среднеквадратичным отклонением результата измерения и определяется по формулегде - i-ый результат наблюдения; - результат измерения (или среднеарифметическое результатов наблюдений); n - число результатов измерений. Следует иметь в виду, что пользоваться этой формулой можно только в случае нормального распределения результатов наблюдений.
Слайд 28Обработка результатов измерений
Точность измерения характеризуется отклонением среднего значения серии измерений
от истинной величины аналитического сигнала. Нетрудно заметить, что это отклонение
определяется систематической и случайной погрешностями измерения.Представляют результаты измерений по стандарту ГОСТ 8.011.
При симметричной доверительной погрешности результаты измерений представляют по форме: , P. При этом числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и значение погрешности Δ.
При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме
, и Р.
Слайд 29Обработка результатов измерений
При испытаниях в технике (особенно в разрушающих
методах измерений) систематической погрешностью часто пренебрегают, и результат
измерений представляют в виде: , коэффициент вариации%, и .
Доверительная вероятность принимается часто
равной P = 0.95 или P = 0.9.
Оценки погрешностей при обработке результатов измерений могут выражаться в абсолютной и относительной формах.
Слайд 30Расслоение данных
Этот приём позволяет какой-либо массив (совокупность) данных разделить, при
необходимости, на отдельные группы по видам факторов, если известно, что
каждое показание в массиве зависит от нескольких факторов.Расслоение целесообразно использовать для варианта, когда одноименные изделия производятся на нескольких, например, резных станках, и всегда при этом существует некоторая разница в характеристиках работы этих станков (разные технические данные станков, разные люди на станках, разное время работы и др.). Эти факторы являются причиной разброса характеристик качества производимых изделий.
Слайд 31Расслоение данных
Можно получить ценную информацию о причинах дефектов, если весь
массив данных по участку разделить (расслоить) по станкам. Можно углубить
анализ, если массив данных делить поочередно по каждому фактору. Рассматривая факторы первого порядка, можно выявить факторы второго порядка и провести расслоение уже по ним. При необходимости и возможности расслоение можно продолжить и для факторов третьего порядка.Слайд 32Расслоение данных
► Метод расслоения в чистом виде используется также
и в финансово-бухгалтерской сфере (при расчётах стоимости изделия, когда требуется
оценка прямых и косвенных расходов отдельно по изделиям и по партиям; при оценке прибыли от продажи изделий отдельно по изделиям и по партиям и т.д.); в сфере маркетинга для оценки поставщиков и потребителей.► Кроме того, расслоение используется и при использовании других статистических методов: при построении причинно-следственных диаграмм, диаграмм Парето, гистограмм и др.
Слайд 33Сравнение выборок
При предварительном анализе данных наблюдений часто возникает необходимость
сравнения двух или нескольких выборок данных, полученных в относительно разных
условиях, чтобы решить одинаковы ли они, принадлежат ли одной генеральной совокупности, и тогда эти выборки при необходимости можно объединять для последующего анализа более мощного массива данных; или же выборки неодинаковы, а значит разница между ними не случайна и выборки не могут быть объединены.Слайд 34Сравнение выборок
Сравнивают выборки по их средним значениям [ 2
]. Однако это сравнение производится по-разному в зависимости от того,
как соотносятся между собой дисперсии этих выборок. Поэтому вначале определяют равны или не равны эти дисперсии.Сравнение двух дисперсий
где в числителе должна быть бо'льшая из двух оценок рассеяния (для того, чтобы значение Fрасч всегда было больше 1).
Критическая область для проверяемой гипотезы при уровне значимости α является односторонней и определяется соотношением F расч и F α . Величину F α определяем при уровне значимости α = 0,05 или α = 0,01
Если F расч < F α , значит дисперсии равны (при этом не значит, чтобы были одинаковыми их численные выражения); если же F расч > F α , то дисперсии считаются не равными, и значит разница между выборками не случайна, и существуют какие-то для этого причины.
Слайд 35Сравнение выборок
Сравнение среднеарифметических
при равных дисперсиях :
Выборки считаются равными, если расчётная величина t оказывается больше, чем
(- t α ), и меньше, чем ( t α ), т.е. находится внутри диапазона: - t α < t расч < t α .Величина t α находится по таблице для t – распределения при уровне значимости α и числе степеней свободы n 1 + n 2 – 2.
Слайд 36Сравнение выборок
Сравнение среднеарифметических
при неравных дисперсиях :
где t α
(n 1 – 1) – значение при n 1 –
1 степенях свободы и уровне значимости α ;t α (n 2 – 1) – значение при n 2 – 1 степенях свободы и уровне значимости α .
Эти значения находят в таблице.
В результате, если расчётная величина t' < t" , то с полным основанием можно говорить о равенстве сравниваемых среднеарифметических величинах.
Слайд 37Гистограммы
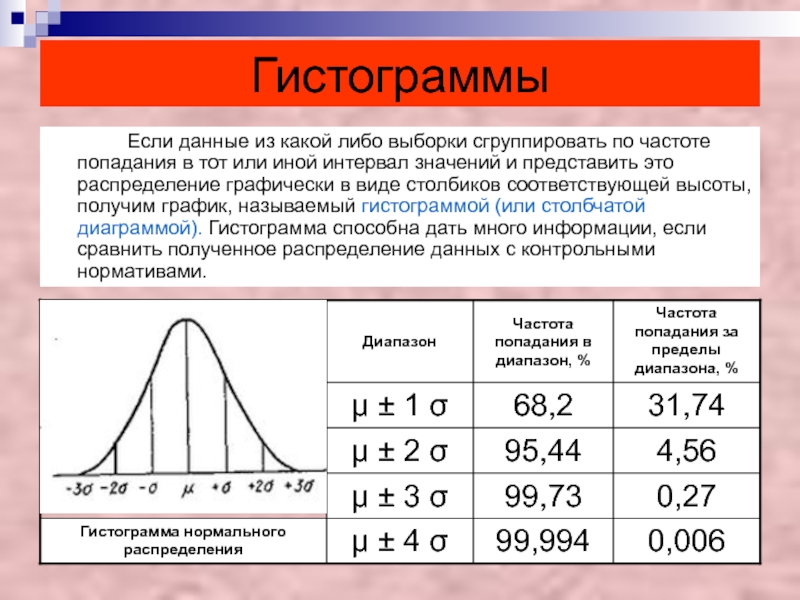
Если данные из какой либо выборки сгруппировать по частоте
попадания в тот или иной интервал значений и представить это
распределение графически в виде столбиков соответствующей высоты, получим график, называемый гистограммой (или столбчатой диаграммой). Гистограмма способна дать много информации, если сравнить полученное распределение данных с контрольными нормативами.Слайд 40Гистограммы
► Существует индекс возможностей (или показатель мощности) процесса, по значению которого
можно делать заключение о состоянии разброса по отношению к допуску;
о том, достаточен ли допуск.В том случае, когда есть и верхняя, и нижняя границы допуска и гистограмма выборки расположена между ними, индекс возможностей процесса С р определяется по формуле:
где S U - верхняя граница допуска,
S L - нижняя граница допуска,
s - стандартное отклонение выборки.
Слайд 41Гистограммы
► Когда С р (или С рк) > 1,67
, значит допуск не менее чем в 10 раз превышает
стандартное отклонение; разброс параметра изделия невелик, появление брака не угрожает. В этом случае можно упростить контроль процесса, что приведёт к снижению себестоимости продукции; можно уменьшить допуск, что будет способствовать улучшению стратегии сбыта.► Если С р < 0,67 , значит допуск не превышает 4-х стандартных отклонений. Процент брака превышает 4,56 %. О таком процессе надо говорить, что он неконтролируем. Необходимо провести сплошной контроль продукции, чтобы не выдавать потребителю
► Когда 1,67 > С р > 1,33 , значит допуск в 8 – 10 раз превышает стандартное отклонение выборки. Состояние процесса считается идеальным.
Слайд 42Временной ряд
Этот приём позволяет простейшим способом представить ход изменения
наблюдаемых данных за определённый период времени. Это могут быть индивидуальные
измерения, средние арифметические выборок, размахи, стандартные отклонения и др. показатели. Наряду с табличной записью данных для наглядности восприятия их наносят на график в той последовательности, в какой они были собраны. То есть этот приём наряду с накоплением требует уже предварительной обработки данных (их группировки, расчёта основных статистических характеристик).Временно'й (динамический) ряд (особенно в графическом виде) позволяет выявлять существенные тенденции в изменении конкретных показаний, их средней величины или разброса данных.
Слайд 43Временной ряд
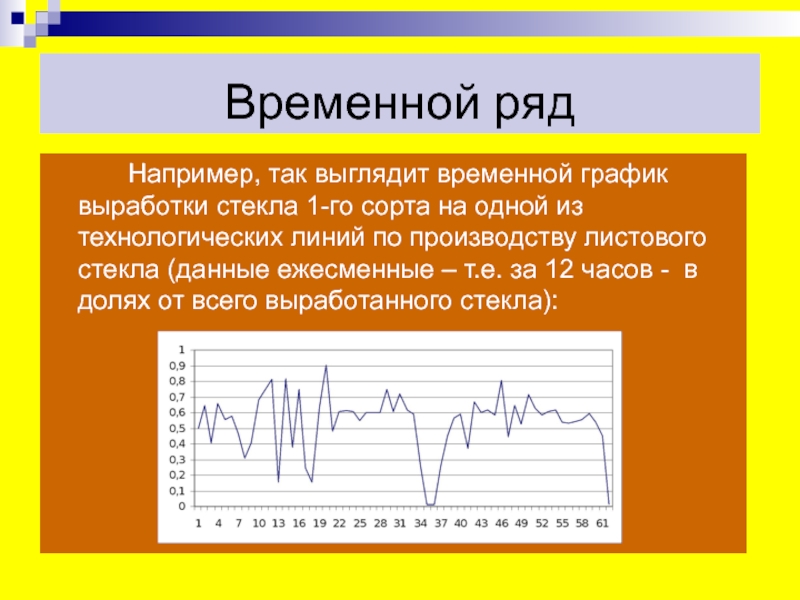
Например, так выглядит временной график выработки стекла
1-го сорта на одной из технологических линий по производству листового
стекла (данные ежесменные – т.е. за 12 часов - в долях от всего выработанного стекла):Слайд 44Временной ряд
Всякий динамический ряд данных теоретически может
быть представлен в виде составляющих :
1) тренд – основная тенденция
развития динамического ряда ( к увеличению или снижению его уровней) ;2) циклические (периодические колебания); случайные колебания.
Методы сглаживания и выравнивания
динамических рядов.
Исключение случайных колебаний значений уровней ряда осуществляется с помощью нахождения «усредненных» значений. Способы устранения случайных факторов делятся на две больше группы: 1. Способы «механического» сглаживания колебаний путем усреднения значений ряда относительно других, расположенных рядом, уровней ряда.
2. Способы «аналитического» выравнивания, т. е. определения сначала функционального выражения тенденции ряда, а затем новых, расчетных значений ряда.
Слайд 45Временной ряд
Методы «механического» сглаживания
а) Метод усреднения
по двум половинам ряда, когда ряд делится на две части.
Затем, рассчитываются два значения средних уровней ряда, по которым графически определяется тенденция ряда. Очевидно, что такой тренд не достаточно полно отражает основную закономерность развития явления.б) Метод укрупнения интервалов, при котором производится увеличение протяженности временных промежутков, и рассчитываются новые значения уровней ряда.
в) Метод скользящей средней. Данный метод применяется для характеристики тенденции развития исследуемой статистической совокупности и основан на расчете средних уровней ряда за определенный период.
Слайд 48Временной ряд
Методы «аналитического» выравнивания
Целью аналитического выравнивания динамического
ряда является определение аналитической или графической зависимости f (t) .
На практике по имеющемуся временному ряду задают вид и находят параметры функции f (t) , а затем анализируют поведение отклонений от тенденции. Функцию f (t) выбирают таким образом , чтобы она давала содержательное объяснение изучаемого процесса .Чаще всего при выравнивании используются зависимости : линейная; параболическая; экспоненциальная. Вариантом решения вопроса выравнивания являются линии регрессии.
Слайд 49Контрольные карты
Для того, чтобы держать процесс в стабильном состоянии, используют
различного вида контрольные карты.
Контрольные карты должны быть выгодны для производства.
Поэтому при их разработке необходимо учитывать:расходы на контроль – они возрастают с увеличением объёма выборки и уменьшаются с сокращением промежутка времени между отбором выборок данных;
расходы, связанные с приостановкой производства – они тем меньше, чем меньше интервал между выборками; поскольку об отклонениях в процессе становится известно раньше, то и времени на устранение причин отклонений потребуется меньше;
расходы, связанные с не обнаруживаемыми отклонениями – чем больше интервал контроля, тем больше вероятность пропустить какое-либо отклонение в процессе.
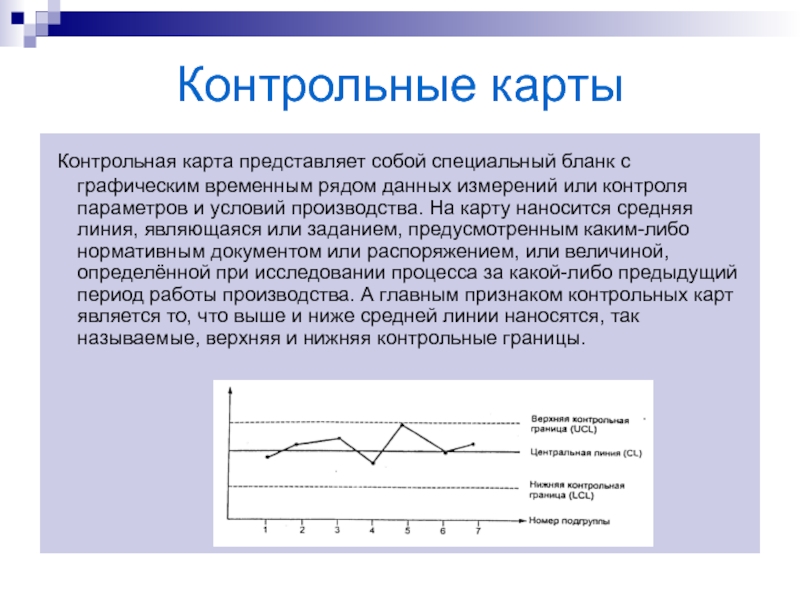
Слайд 50Контрольные карты
Контрольная карта представляет собой специальный бланк с графическим
временным рядом данных измерений или контроля параметров и условий производства.
На карту наносится средняя линия, являющаяся или заданием, предусмотренным каким-либо нормативным документом или распоряжением, или величиной, определённой при исследовании процесса за какой-либо предыдущий период работы производства. А главным признаком контрольных карт является то, что выше и ниже средней линии наносятся, так называемые, верхняя и нижняя контрольные границы.Слайд 51Контрольные карты
Стандартом ГОСТ Р 50779.42 (ИСО 8258-91) предусмотрены две группы
контрольных карт:
а) контрольные карты для количественных данных:
*
карты средних () и размахов (R) или выборочных стан-дартных отклонений (s);
* карта индивидуальных значений (X) и скользящих разма-
хов (R);
* карта медиан (Ме) и размахов (R);
б) контрольные карты для альтернативных данных:
* карта долей несоответствующих единиц продукции (p) или
карта числа несоответствующих единиц (np);
* карта числа несоответствий (с) или карта числа несоответ-
ствий, приходящихся на единицу продукции (u).
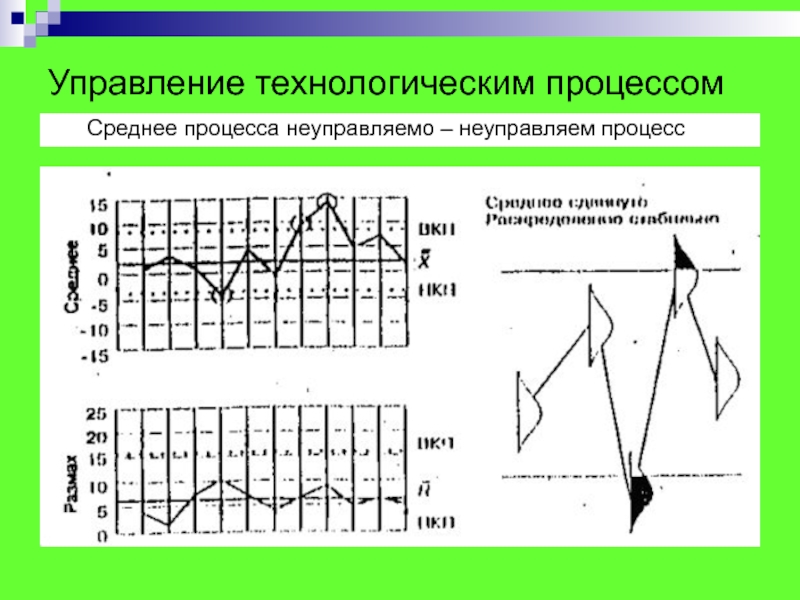
Слайд 52Управление технологическим процессом
Для управления процессами используют статистические сигналы о
наличии особых (н е с л у ч а й
н ы х) причин вариаций. Постоянное установление, а затем и устранение этих особых причин чрезмерной изменчивости процесса приводит его в состояние статистической управляемости. Если процесс находится в статистически управляемом состоянии, качество продукции предсказуемо, и процесс пригоден для удовлетворения требований, установленных в нормативных документах.Наиболее часто используют две карты (средних и размахов). Они отражают четыре варианта условий протекания техпроцесса:
Слайд 54Управление технологическим процессом
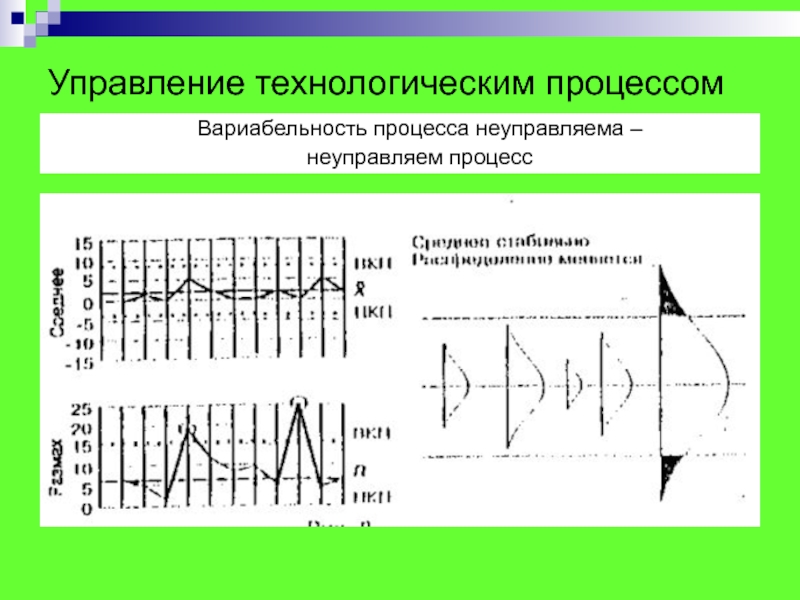
Вариабельность процесса неуправляема –
неуправляем процесс
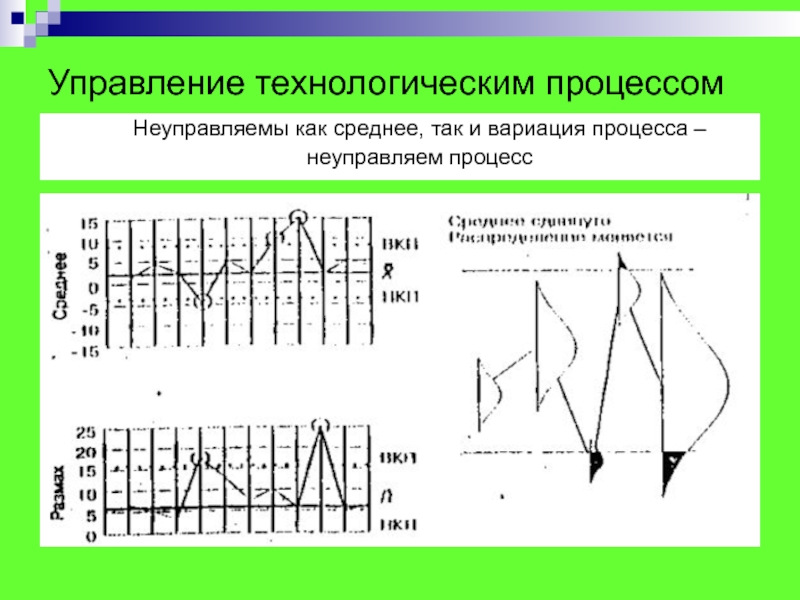
Слайд 55Управление технологическим процессом
Неуправляемы как среднее, так и вариация процесса –
неуправляем процесс
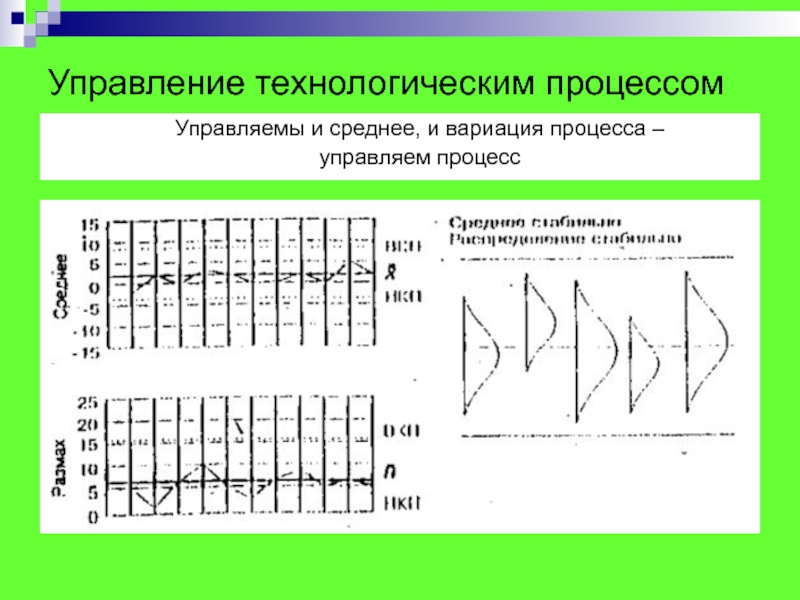
Слайд 56Управление технологическим процессом
Управляемы и среднее, и вариация процесса –
управляем
процесс
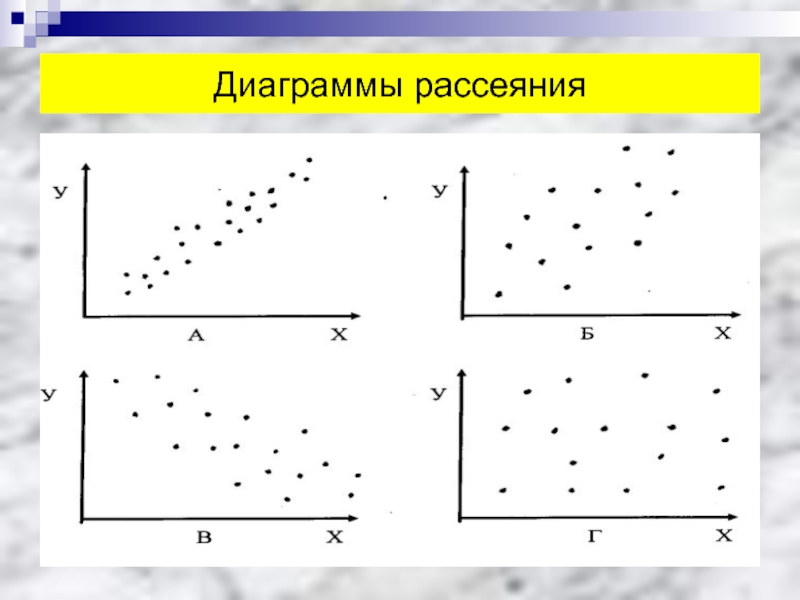
Слайд 58Диаграммы рассеяния
Диаграмма разброса, также как и метод расслоения, используется для
выявления причинно-следственных связей показателей качества и влияющих факторов при анализе
причинно-следственных связей. Анализ диаграмм разброса или оценка корреляционной взаимосвязи параметров является важнейшей частью корреляционно-регрессионного анализа.С помощью диаграммы выясняется, имеется ли между этими двумя параметрами корреляционная зависимость (иначе говоря, взаимосвязанная изменчивость).
Корреляция может быть п р я м о й (при увеличении одного параметра увеличивается и другой) и о б р а т н о й или отрицательной (при увеличении одного параметра другой при этом уменьшается). Корреляция может быть т е с н о й (сильной) или л ё г к о й (слабой). Наконец, корреляция может быть к р и в о л и н е й н о й.
Слайд 61Корреляция
Оценивают степень тесноты (значимость) корреляционной зависимости различными методами.
Так, можно вычислить коэффициент корреляции по формуле:
r = Где – значения параметров х и у для i-го измерения;
- средние арифметические значения величин х и у;
– стандартные отклонения величин х и у;
n – число измерений в выборке (объём выборки).
Чем ближе коэффициент корреляции к ±1 (плюс - прямая, минус - обратная связь), тем теснее зависимость между параметрами. Если r = 0 , корреляционная зависимость отсутствует.
Слайд 63Регрессионный анализ
Если корреляционный анализ на основе диаграмм разброса позволяет установить
наличие и оценить степень тесноты взаимосвязи двух и более параметров,
то регрессионный анализ позволяет выразить установленную взаимосвязь в виде уравнения регрессии, которое кроме возможности рассчитывать характеристику (или результат) у по одному или многим факторам (или причинам) х , даёт тоже достаточно много информации о характере и степени тесноты между исследуемыми параметрами.Для регрессионного анализа используют данные а к т и в н ы х экспериментов, в ходе которых «раскачивают» технологический процесс, и данные п а с с и в н ы х экспериментов, т.е. результаты текущих наблюдений за процессом. При этом в первом случае возможна «порча» продукции; во втором случае в процесс не вмешиваются, за ним только наблюдают.
Слайд 64Регрессионный анализ
Найти линию регрессии, наиболее адекватно отражающую облако точек –
основная задача регрессионного анализа. Естественно, наименьший разброс точек будет около
той линии, которая определяется по коррелированным параметрам.Главное в регрессионном анализе то, что исследователь сам задаёт вид линии регрессии.
Рассмотрим поиск адекватного уравнения на примере уравнений регрессии между содержанием в стекле оксида Fe 2 O 3 (F) и светопропусканием стекла в ИК-области спектра (D) по экспериментальным данным (пассивный эксперимент !), представленным в ранее рассмотренной диаграмме рассеяния. По этой диаграмме мы установили, что связь между этими параметрами существует. Но какая: линейная или криволинейная? – неизвестно.
Слайд 65Регрессионный анализ
Начинают анализ с самой простой формы связи – линейной,
которая выражается уравнением регрессии 1-ой степени и имеет вид
Составляем систему
уравненийНа основе экспериментальных данных подсчитываются соответствующие суммы и подставляются в уравнения системы.
Слайд 66Регрессионный анализ
Решение системы
уравнений
методом вычитания
уравнения
С помощью
программы Solver
После решения приведённой ранее системы
уравнений
получим уравнение 1-ой степени
D = 0,92181 – 1,0 F
.Слайд 67Регрессионный анализ
Теперь необходимо оценить, насколько полученное уравнение адекватно экспериментальным
данным. Для этого используют критерий, тоже называемый коэффициентом корреляции, но
определяемый иначе:Для нашего примера после расчёта дисперсий получим следующее значение коэффициента корреляции R = 0.4899.
Слайд 68Регрессионный анализ
Одно из правил оценки адекватности линий регрессии гласит, что
дисперсия расчётных по уравнению регрессии данных относительно экспериментальных должна быть
на порядок меньше дисперсии экспериментальных данных относительно их средней арифметической (или коэффициент корреляции должен быть больше 0,9 - при хорошо коррелированных параметрах).Слайд 69Регрессионный анализ
Как и следовало ожидать, судя по диаграмме разброса,
адекватность расчётных и экспериментальных данных мала, а поэтому необходимо продолжить
анализ и рассчитать уравнение регрессии 2-ой степени вида:Составим опять систему уравнений:
Подставив в эту систему уравнений численные значения сумм экспериментальных данных и решив эту систему уравнений, получим
коэффициенты регрессии для уравнения 2-ой степени:
Слайд 70Регрессионный анализ
D = 0.916211 – 0.976872 F – 0.012245 F
2 .
Для этого уравнения коэффициент корреляции R = 0,6678.
Если бы
мы таким же образом рассчитали уравнение регрессии 3-ей степени (кубическая парабола) вида :то получили бы следующее уравнение:
D = 0.866938 – 0.64025 F – 0.553823 F 2 – 0.113272 F 3 .
Рассчитав по этому уравнению расчётную дисперсию, получим коэффициент корреляции R = 0,6668.
Делаем вывод, что уравнение 3-ей степени в нашем случае менее адекватно, чем уравнения 2-ой степени, будучи и более сложным в использовании. А поэтому результатом регрессионного анализа принимаем уравнение 2-ой степени.
Слайд 73
Для управления качеством продукции на производстве специалисты привлекают всё более
и более новые методы анализа.
Как показывает исторический опыт, именно нетрадиционные
подходы к решению тех или иных задач, объяснению разнообразных явлений способствовали развитию цивилизации (закон всемирного притяжения, который возник в результате качественного отождествления «яблока» и земного шара, нелинейные пространства Лобачевского и др.).Слайд 74Ф С А
В экономическом анализе также возникали подобные идеи, в
частности функционально-стоимостный анализ (ФСА), который первоначально разрабатывался как метод поиска
резервов сокращения затрат на производство.ФСА же основывается на следующем утверждении: каждый продукт или объект производится и существует для удовлетворения определенных потребностей (выполнения своих функций): часы — чтобы показывать время, телевизор — чтобы принимать видеосигнал и преобразовывать его в изображение, карандаш — чтобы писать или рисовать и т.д. Известно, что для создания этих функций в продукте или товаре нужно затрачивать определенное количество живого и овеществленного труда.
Слайд 75Ф С А
В промышленно развитых странах предприятиями, работающими в условиях
сильнейшей конкуренции товаров и их качества, накоплен огромный опыт по
созданию, совершенствованию и применению различных методов по предупреждению появления ошибок и устранению их первопричин. Из литературы известен один из наиболее эффективных методов – метод FMEA – на современном уровне его развития и применения.Это – метод систематической оценки потенциальных отказов и устранения причин их появления (о целесообразности использования которого указано в элементе 8 МС ИСО 9004-1)
Слайд 76F M E A
Применение метода FMEA обусловлено следующими причинами:
Необходимость для
предприятия создания высокотехнологичного продукта, обеспечивающего достижение жизненно важно цели производства
– продукции без брака.Необходимость строго следовать таким нормам, как ИСО 9001 (элементы 4.4 – проектирование, 4.9 – производство, 4.20 – статистические методы), а также требованиям законов по защите прав потребителей, безопасности потребителей и окружающей среды.
Возрастающие требования заказчиков к безотказности продукции, приспособленности к условиям эксплуатации, сервису и др.
Обостряющаяся конкуренция.
Слайд 77F M E A
В книге «Оценка риска и последствий отказов
комплексной системы, конструкции, процессов» рассмотрены основные принципы организации работ на
предприятии по практическому применению метода FMEA. Приводится справочный материал, а также примеры анализа. Особое внимание обращается на наиболее сложные и важные положения по проведению FMEA такие, как функциональный анализ, отбор элементов для FMEA, определение вероятности отказов и др. Основные ключевые положения и цели метода FMEA выделены в виде соответствующих рисунков и подписей к ним.Книга рекомендуется в качестве практического пособия для инженерно-технического персонала предприятий, занимающегося созданием систем, конструкций и процессов. Она может быть использована при обучении инженерно-технических работников предприятий и студентов вузов. Авторы очень надеются, что книга окажется полезной и для руководителей предприятий.



























![Презентация к консп. лекц_2.ppt Сравнение выборок Сравнивают выборки по их средним значениям [ 2 ]. Сравнение выборок Сравнивают выборки по их средним значениям [ 2 ]. Однако это сравнение производится по-разному в](/img/thumbs/e4b742ba3e53b4a85f3a2cad4e538af4-800x.jpg)