Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Деревья.ppt
Содержание
- 1. Деревья.ppt
- 2. Древовидная структура характеризуется множеством узлов (nodes), происходящих
- 3. Каждый узел дерева является корнем поддерева (subtree),
- 4. Бинарные деревья-деревья, где каждый родитель имеет не
- 5. Вырожденные деревья являются крайней мерой плотности. Другая
- 6. Структура бинарного дерева построена из узлов. Эти
- 7. Если дерево организовано таким образом, что для
- 8. АВЛ-деревьяТак исторически сложилось, что у этих деревьев
- 9. При операциях добавления и удаления может произойти
- 10. Малое левое вращениеПусть показатель сбалансированности вершины, в
- 11. Слайд 11
- 12. Большое левое вращениеНесколько сложнее случай, когда показатель
- 13. Восстановление сбалансированностиПусть имеется дерево, сбалансированное всюду, кроме
- 14. Задание (номер варианта задания соответствует вашему номеру
- 15. 7. Написать процедуру, которая выводит на экран
- 16. 12. Отсортировать массив А путем включения его
- 17. 16. Напишите программу, содержащую процедуру или функцию,
- 18. Порядок выполнения работыПорядок выполнения работыПеред выполнением индивидуального
- 19. Требования к отчетуТребования к отчетуОтчет должен содержать:1.
- 20. Контрольные вопросыКонтрольные вопросы1. Что такое дерево, двоичное
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Информатика
Лабораторная работа № 23
эффективного хранения и обработки информации на примере деревьев.
Слайд 2
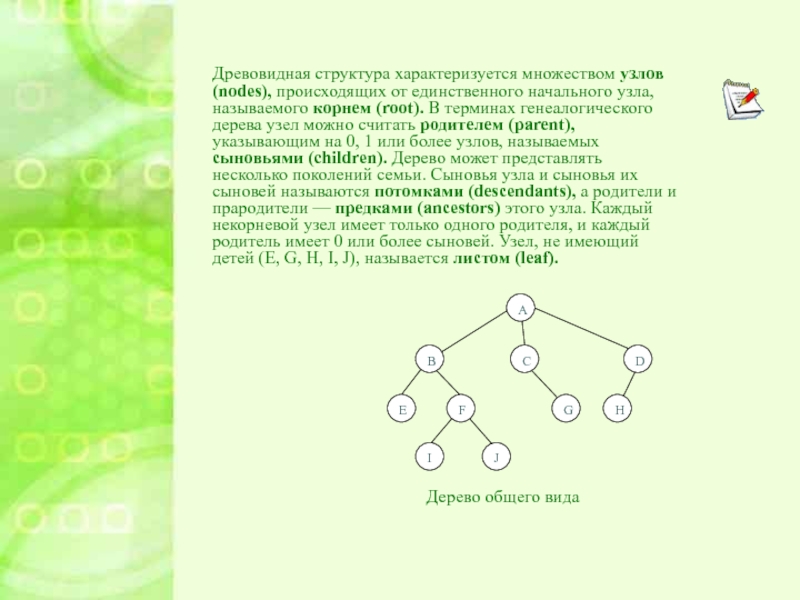
Древовидная структура характеризуется множеством узлов (nodes), происходящих от единственного начального
узла, называемого корнем (root). В терминах генеалогического дерева узел можно
считать родителем (parent), указывающим на 0, 1 или более узлов, называемых сыновьями (children). Дерево может представлять несколько поколений семьи. Сыновья узла и сыновья их сыновей называются потомками (descendants), а родители и прародители — предками (ancestors) этого узла. Каждый некорневой узел имеет только одного родителя, и каждый родитель имеет 0 или более сыновей. Узел, не имеющий детей (Е, G, H, I, J), называется листом (leaf).
Дерево общего вида
Слайд 3
Каждый узел дерева является корнем поддерева (subtree), которое определяется данным
узлом и всеми потомками этого узла.
Глубина дерева есть длина
самого длинного пути от корня до узла.Слайд 4
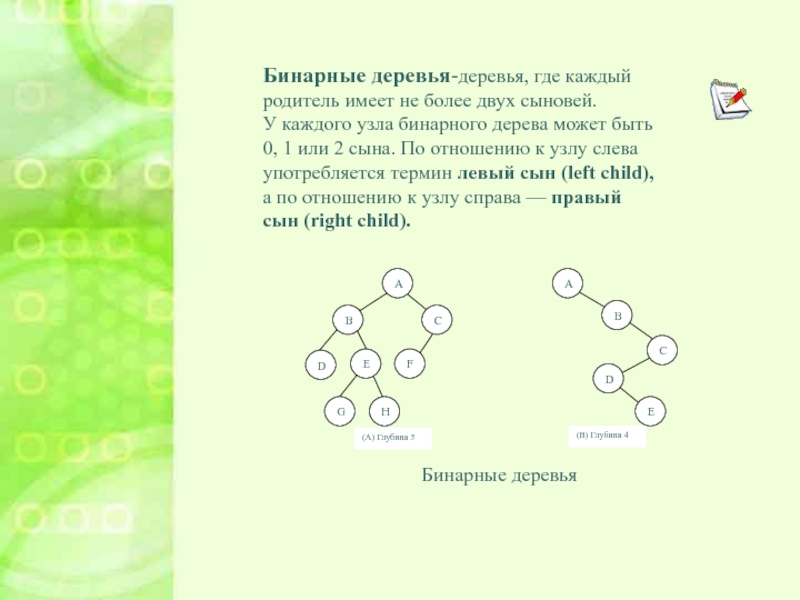
Бинарные деревья-деревья, где каждый родитель имеет не более двух сыновей.
У
каждого узла бинарного дерева может быть 0, 1 или 2
сына. По отношению к узлу слева употребляется термин левый сын (left child), а по отношению к узлу справа — правый сын (right child).Бинарные деревья
Слайд 5
Вырожденные деревья являются крайней мерой плотности. Другая крайность — законченные
бинарные деревья (complete binary tree) глубины N, где каждый уровень
0...N-1 имеет полный набор узлов и все листья уровня N расположены слева. Законченное бинарное дерево, содержащее 2N узлов на уровне N является полным (full). На рисунке показаны законченное и полное бинарные деревья.Слайд 6
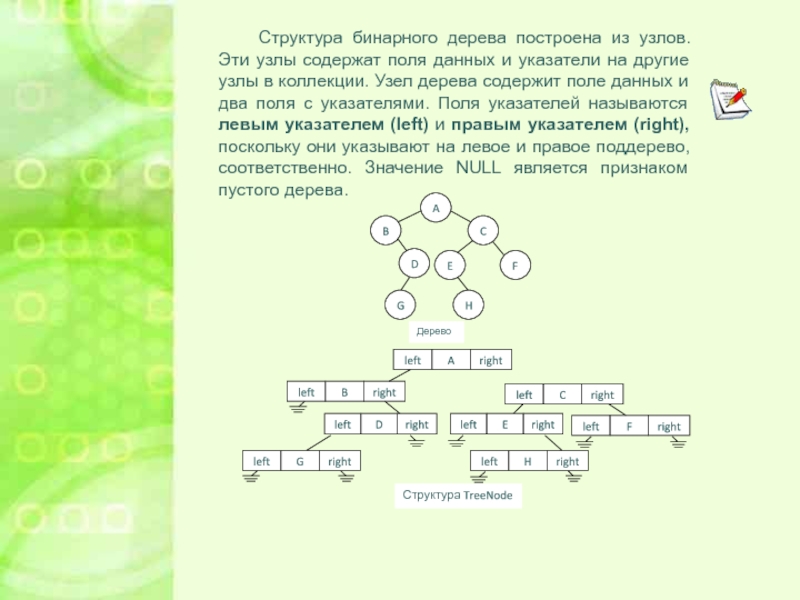
Структура бинарного дерева построена из узлов. Эти узлы содержат поля
данных и указатели на другие узлы в коллекции. Узел дерева
содержит поле данных и два поля с указателями. Поля указателей называются левым указателем (left) и правым указателем (right), поскольку они указывают на левое и правое поддерево, соответственно. Значение NULL является признаком пустого дерева.Слайд 7
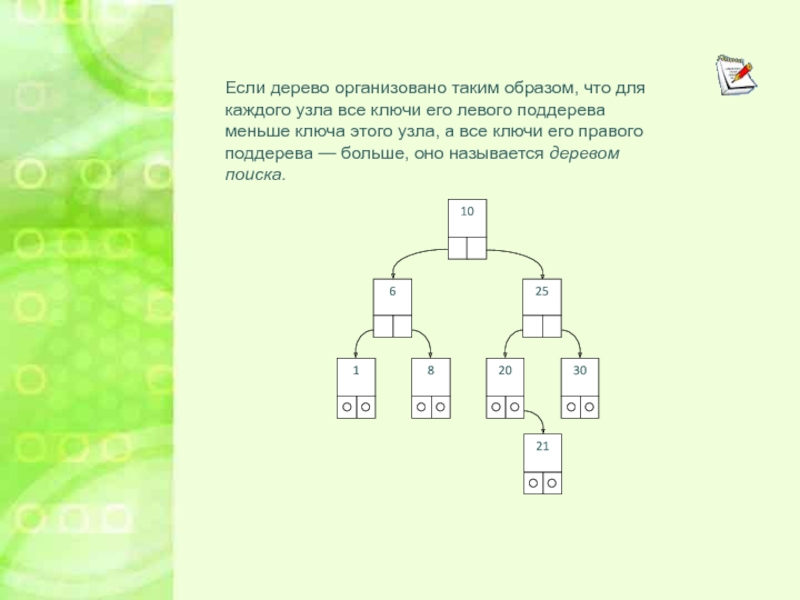
Если дерево организовано таким образом, что для каждого узла все
ключи его левого поддерева меньше ключа этого узла, а все
ключи его правого поддерева — больше, оно называется деревом поиска.Слайд 8
АВЛ-деревья
Так исторически сложилось, что у этих деревьев есть два альтернативных
названия: АВЛ-деревья и сбалансированные деревья. АВЛ произошло от фамилий изобретателей(Г.М.Адельсоном-Вельским
и Е.М.Ландисом). Идеально сбалансированным называется дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более, чем на 1.Г.М.Адельсон-Вельский
Е.М.Ландис
Слайд 9
При операциях добавления и удаления может произойти нарушение сбалансированности дерева.
В этом случае потребуются некоторые преобразования, не нарушающие упорядоченности дерева
и способствующие лучшей сбалансированности.В сбалансированном дереве показатели сбалансированности всех вершин лежат в пределах от -1 до 1. При операциях добавления/удаления могут появляться вершины с показателями сбалансированности -2 и 2.
Вращения
Слайд 10
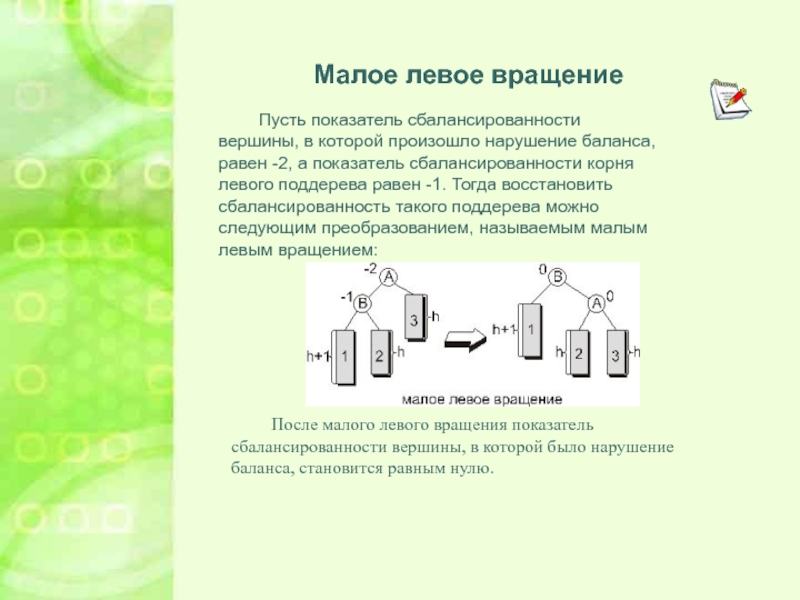
Малое левое вращение
Пусть показатель сбалансированности вершины, в которой произошло нарушение
баланса, равен -2, а показатель сбалансированности корня левого поддерева равен
-1. Тогда восстановить сбалансированность такого поддерева можно следующим преобразованием, называемым малым левым вращением:После малого левого вращения показатель сбалансированности вершины, в которой было нарушение баланса, становится равным нулю.
Слайд 12
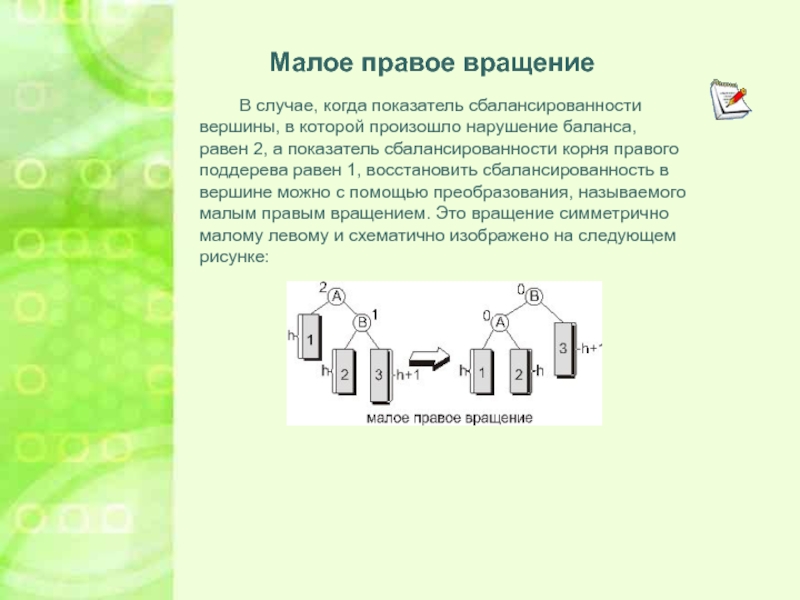
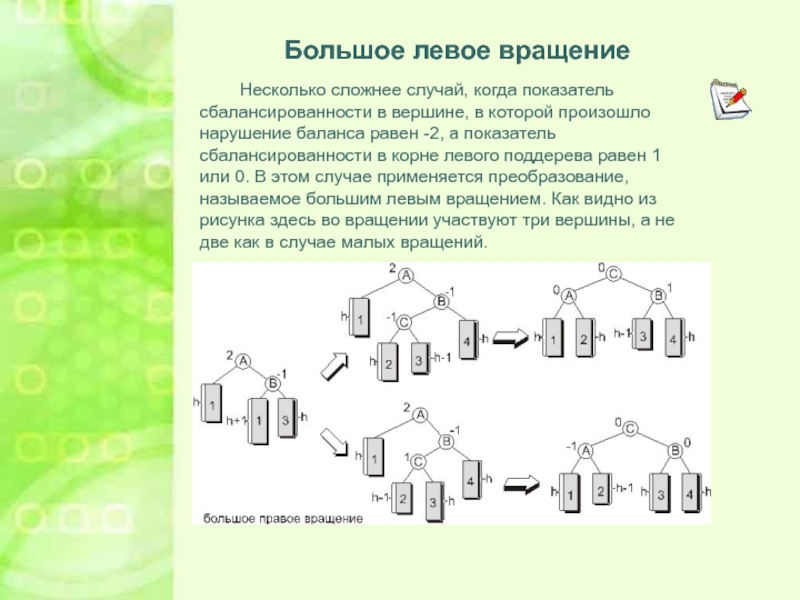
Большое левое вращение
Несколько сложнее случай, когда показатель сбалансированности в вершине,
в которой произошло нарушение баланса равен -2, а показатель сбалансированности
в корне левого поддерева равен 1 или 0. В этом случае применяется преобразование, называемое большим левым вращением. Как видно из рисунка здесь во вращении участвуют три вершины, а не две как в случае малых вращений.Слайд 13
Восстановление сбалансированности
Пусть имеется дерево, сбалансированное всюду, кроме корня, а в
корне показатель сбалансированности по модулю равен 2-м. Такое дерево можно
сбалансировать с помощью одного из четырех вращений. При этом высота дерева может уменьшиться на 1. Для восстановления баланса после удаления/добавления вершины надо пройти путь от места удаления/добавления до корня дерева, проводя при необходимости перебалансировку и изменение показателя сбалансированности вершин вдоль пути к корню.Слайд 14Задание (номер варианта задания соответствует вашему номеру в журнале)
Задание (номер
варианта задания соответствует вашему номеру в журнале)
1. Написать рекурсивную числовую
функцию, подсчитывающую сумму элементов дерева. 2. Написать функцию, которая находит наибольший элемент дерева.
3. Написать функцию, которая находит наименьший элемент дерева.
4. Напишите процедуру, которая удаляет из дерева все четные элементы.
5. Написать рекурсивную процедуру, которая определяет число вхождений заданного элемента в дерево.
6. Написать рекурсивную процедуру, которая печатает элементы из всех листьев дерева.
Слайд 157. Написать процедуру, которая выводит на экран дерево, показывая глубину
узлов отступом от левого края экрана. Например, дерево
7. Написать процедуру,
которая выводит на экран дерево, показывая глубину узлов отступом от левого края экрана. Например, дерево1 группа
1 курс
2 группа
ФМИ
3 группа
2 курс
4 группа
8. Написать рекурсивную функцию, которая определяет глубину заданного элемента на дереве и возвращает –1, если такого элемента нет.
9. Написать процедуру, которая печатает (по одному разу) все вершины дерева.
10. Написать процедуру, которая по заданному n считает число всех вершин глубины n в заданном дереве.
11. Написать процедуру, которая считает глубину дерева.
Слайд 1612. Отсортировать массив А путем включения его элементов в дерево
и скопировать отсортированные данные обратно в А.
13. Задана последовательность
слов. Определить частоту вхождения каждого из слов в последовательность. Указание. Для решения задачи любое слово ищется в дереве, которое на начальном этапе пусто. Если слово найдено, то счетчик его вхождений увеличивается на единицу, если нет, то слово включается в дерево с единичным значением счетчика.
14. Написать программу представления бинарного дерева с помощью динамических структур (запрограммировать стандартные операции: добавление, удаление элемента, просмотр дерева). Запрограммировать специальную функцию, которая определяет значение листа двоичного дерева, имеющего минимальную глубину
15. Организовать хранение сбалансированного дерева в памяти ЭВМ, а также реализовать основные операции над сбалансированным деревом: поиск/добавление/удаление.
12. Отсортировать массив А путем включения его элементов в дерево и скопировать отсортированные данные обратно в А.
13. Задана последовательность слов. Определить частоту вхождения каждого из слов в последовательность.
Указание. Для решения задачи любое слово ищется в дереве, которое на начальном этапе пусто. Если слово найдено, то счетчик его вхождений увеличивается на единицу, если нет, то слово включается в дерево с единичным значением счетчика.
14. Написать программу представления бинарного дерева с помощью динамических структур (запрограммировать стандартные операции: добавление, удаление элемента, просмотр дерева). Запрограммировать специальную функцию, которая определяет значение листа двоичного дерева, имеющего минимальную глубину
15. Организовать хранение сбалансированного дерева в памяти ЭВМ, а также реализовать основные операции над сбалансированным деревом: поиск/добавление/удаление.
Слайд 1716. Напишите программу, содержащую процедуру или функцию, которая подсчитывает число
вершин на каждом уровне непустого дерева (корень считать вершиной 0-го
уровня). В программе используйте подпрограммы.17. Напишите программу, содержащую процедуру или функцию, которая определяет максимальную глубину непустого дерева Т, т.е. число ветвей в самом длинном из путей от корня дерева до листьев.
18. Постройте два дерева. Проверьте, является ли одно из них поддеревом другого. Если "нет", то включите это поддерево. В программе используйте подпрограммы.
19. Написать программу формирования дерева. Удалите из дерева все повторяющиеся элементы. В программе используйте подпрограммы.
20. Объедините два дерева в одно идеально сбалансированное. В программе используйте подпрограммы.
16. Напишите программу, содержащую процедуру или функцию, которая подсчитывает число вершин на каждом уровне непустого дерева (корень считать вершиной 0-го уровня). В программе используйте подпрограммы.
17. Напишите программу, содержащую процедуру или функцию, которая определяет максимальную глубину непустого дерева Т, т.е. число ветвей в самом длинном из путей от корня дерева до листьев.
18. Постройте два дерева. Проверьте, является ли одно из них поддеревом другого. Если "нет", то включите это поддерево. В программе используйте подпрограммы.
19. Написать программу формирования дерева. Удалите из дерева все повторяющиеся элементы. В программе используйте подпрограммы.
20. Объедините два дерева в одно идеально сбалансированное. В программе используйте подпрограммы.
Слайд 18Порядок выполнения работы
Порядок выполнения работы
Перед выполнением индивидуального задания ознакомиться с
тем, что такое дерево, упорядоченное дерево, идеально сбалансированное дерево и
дерево, сбалансированное по АВЛ, изучить управление таким деревом, анализ алгоритмов управления.При выполнении индивидуального задания придерживаться следующей последовательности действий:
- изучить словесную постановку задачи;
- разработать программу, решающую поставленную задачу;
- оттестировать и отладить программу;
- написать и представить к защите отчет по работе.
Слайд 19Требования к отчету
Требования к отчету
Отчет должен содержать:
1. Цель работы
2. Задание
3.
Программа
4. Результат выполнения работы программы
5. Ответы на контрольные вопросы
6. Вывод
Слайд 20Контрольные вопросы
Контрольные вопросы
1. Что такое дерево, двоичное дерево, поддерево?
2. Приведите
два способа хранения деревьев в памяти ЭВМ, укажите их недостатки
и достоинства.3. Приведите определение идеально сбалансированного дерева и дерева сбалансированного по АВЛ.
4. Что такое вращения и для чего они применяются?