Призма

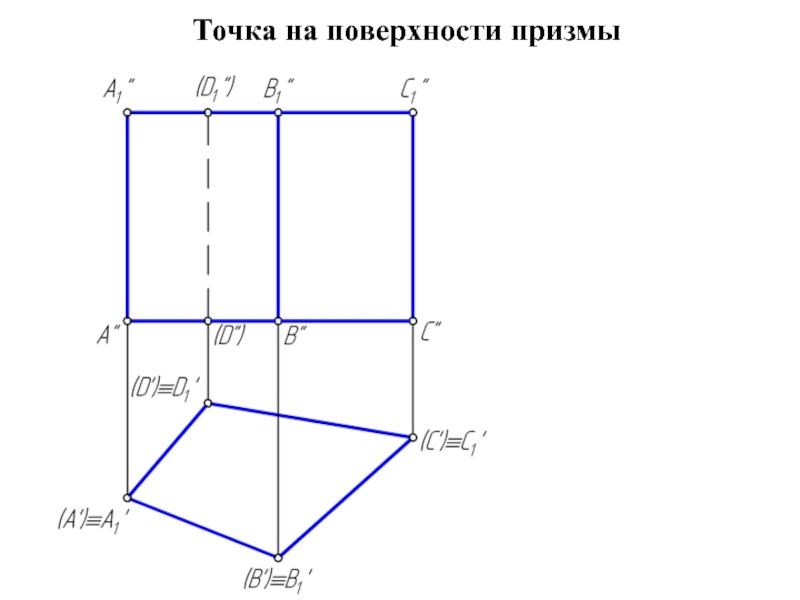
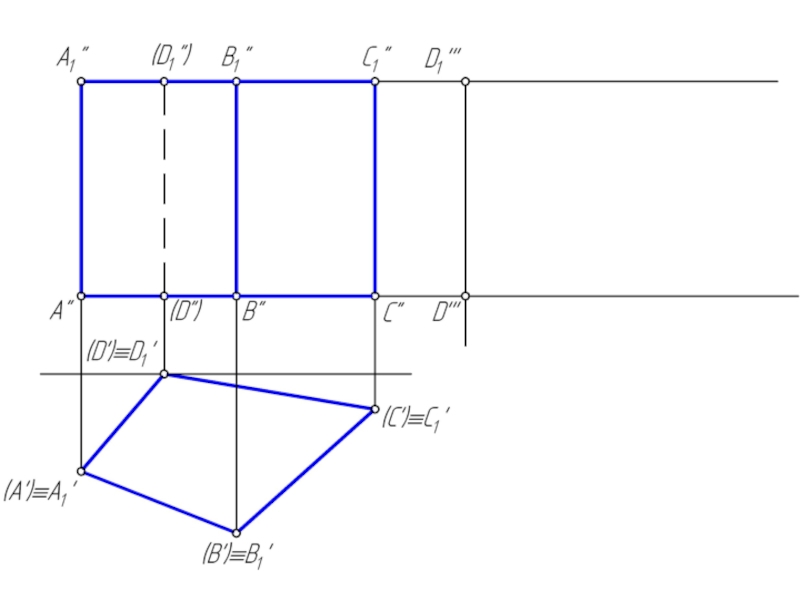
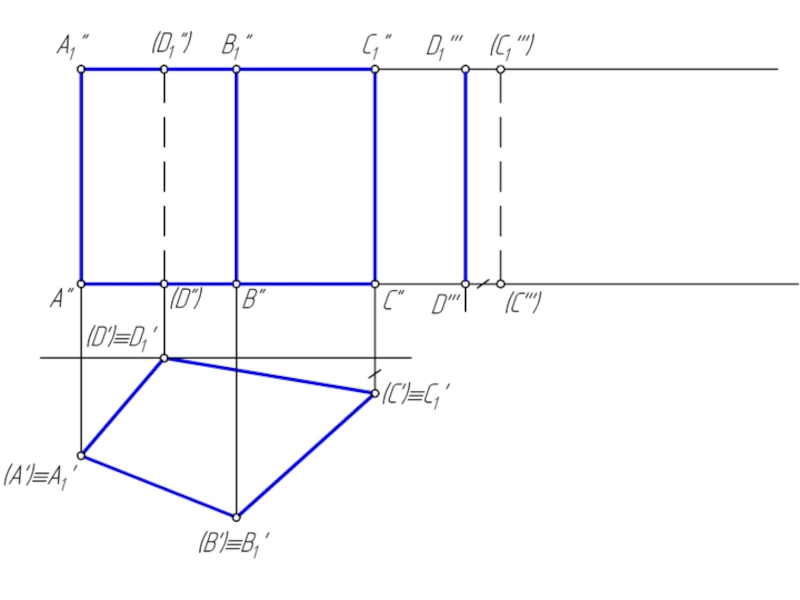
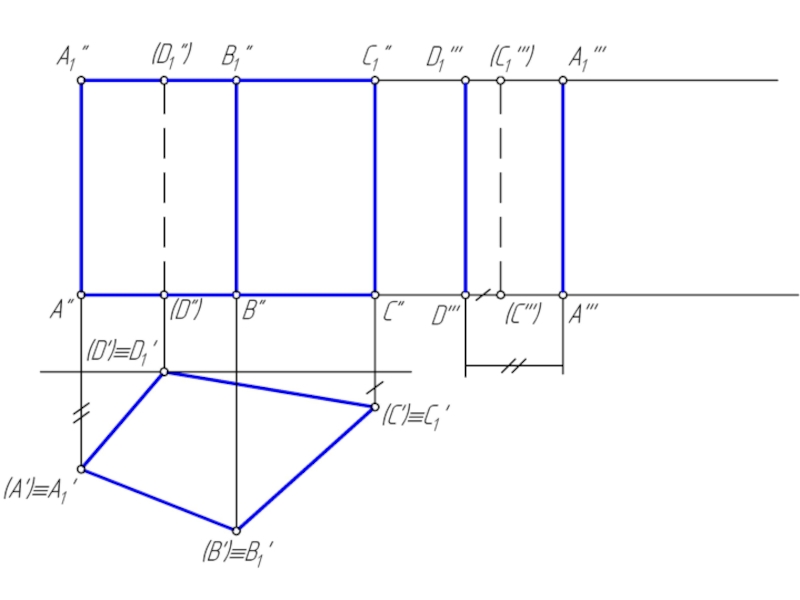
пространственную фигуру, ограниченную со всех сторон плоскими многоугольниками.
Вершины многоугольников

являются вершинами многогранника.
Стороны многоугольников образуют ребра.
Плоскости многоугольников – грани многогранника.
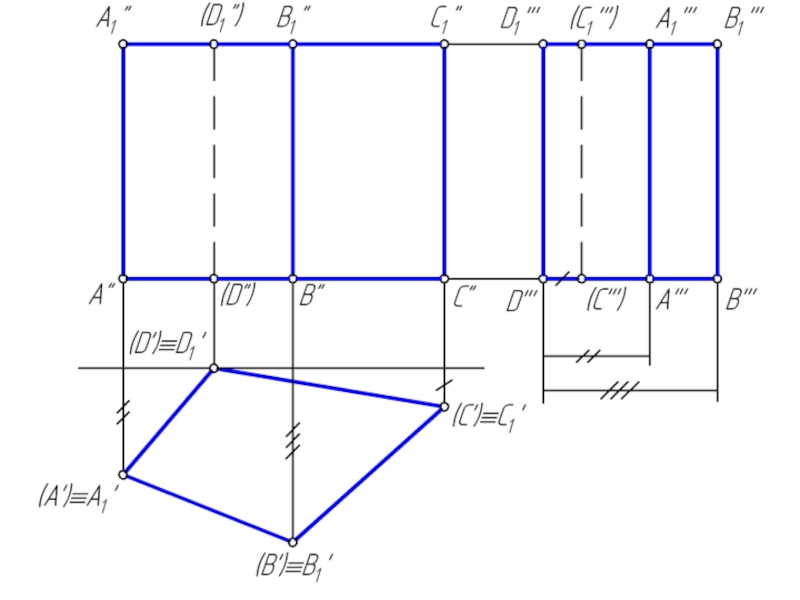
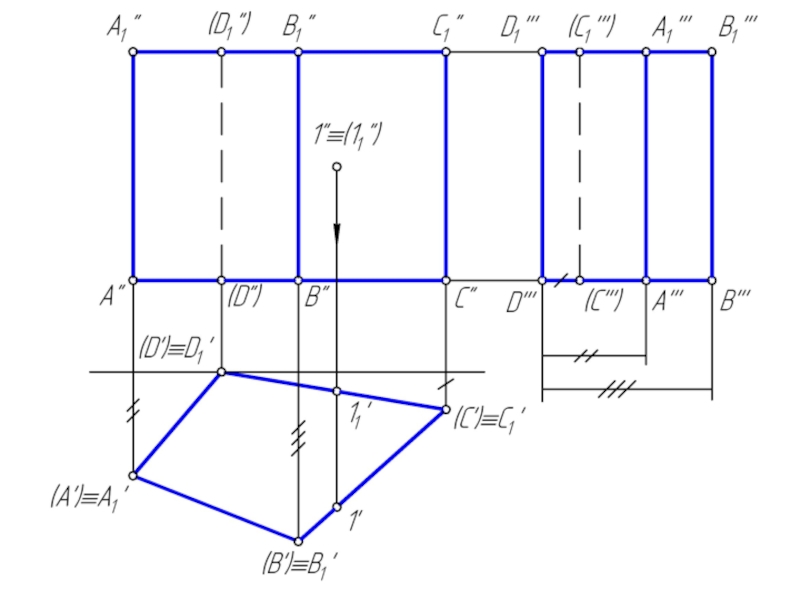
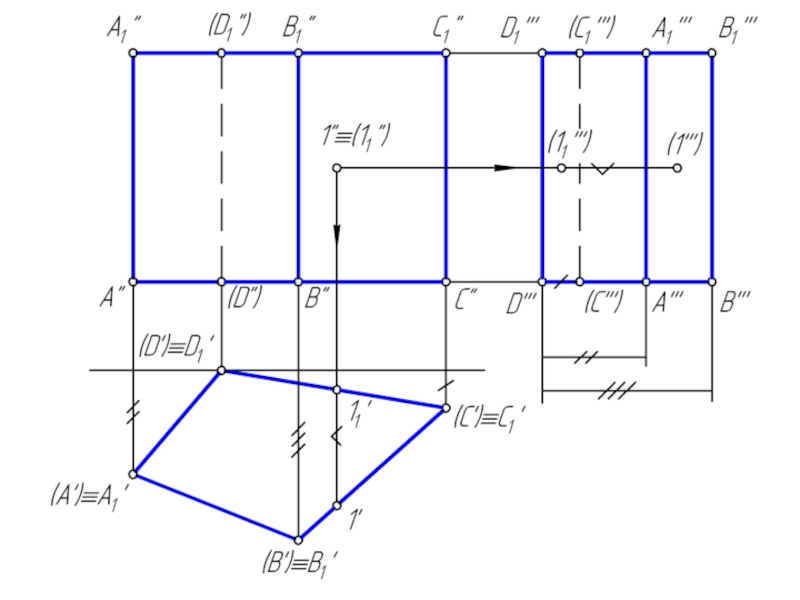
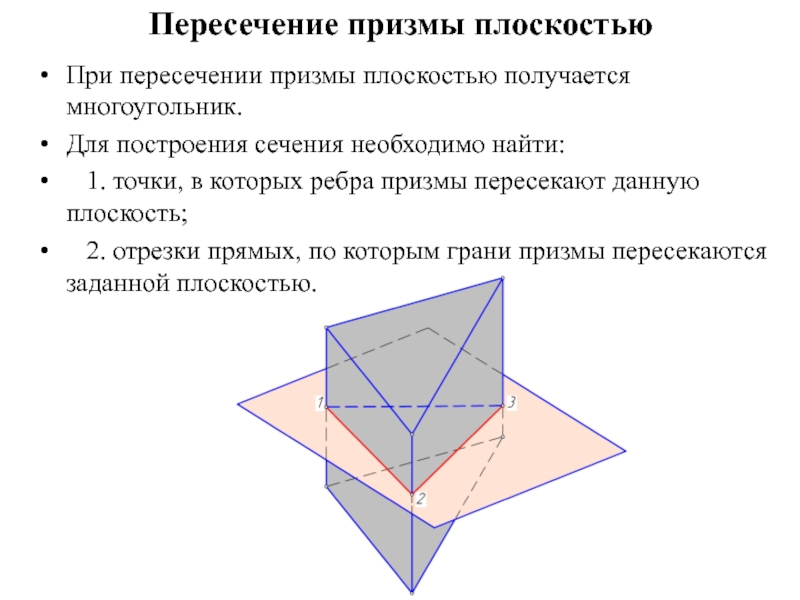
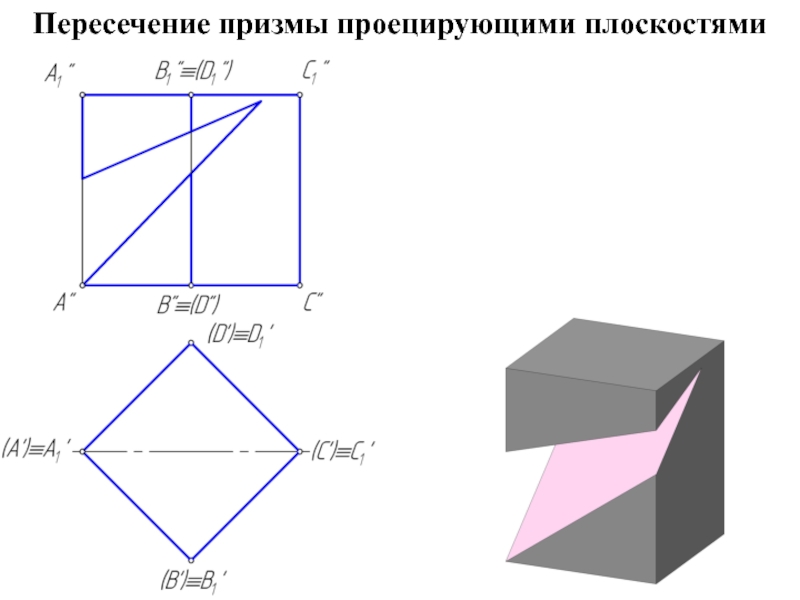
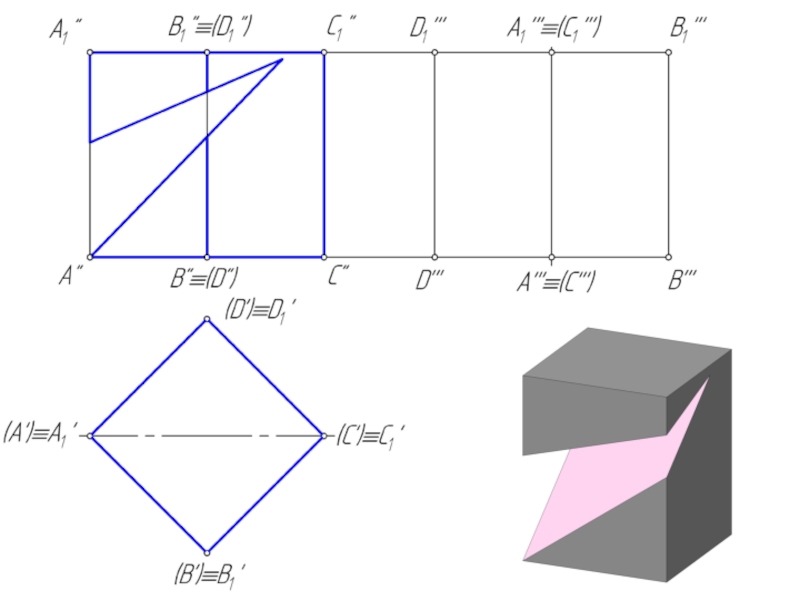
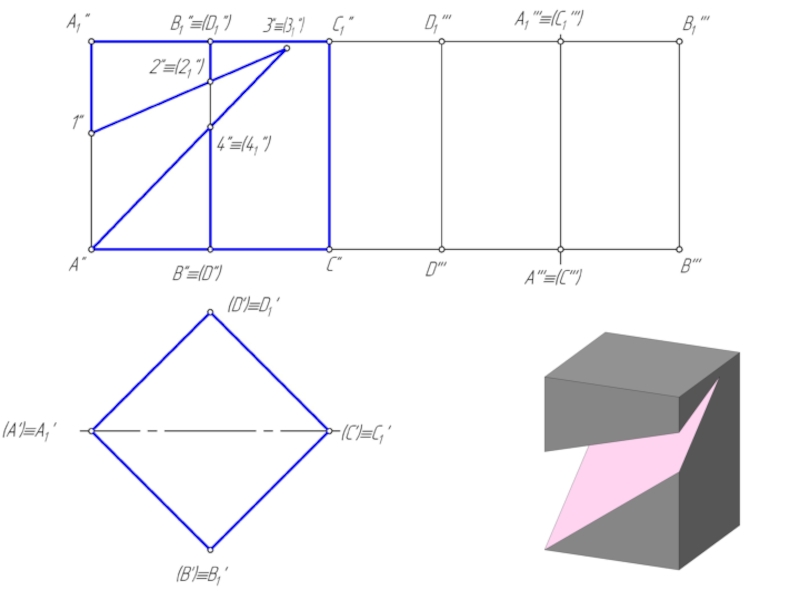
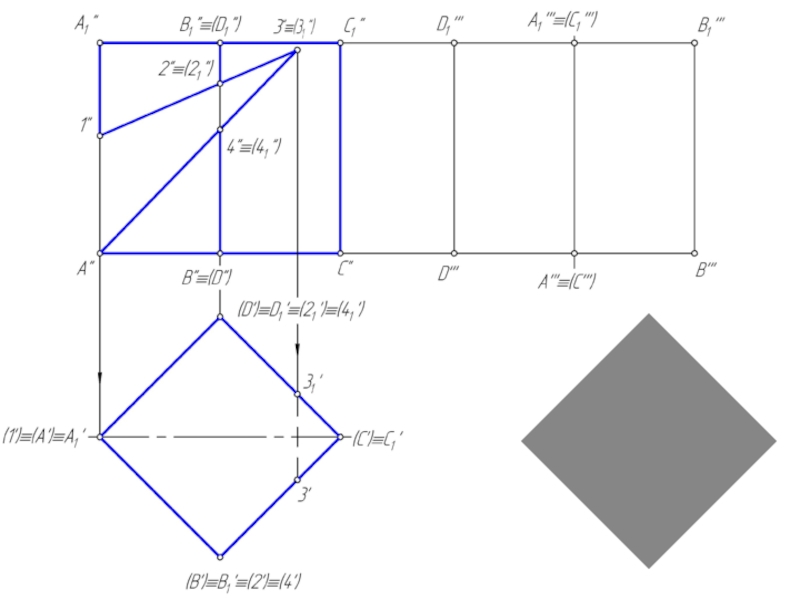
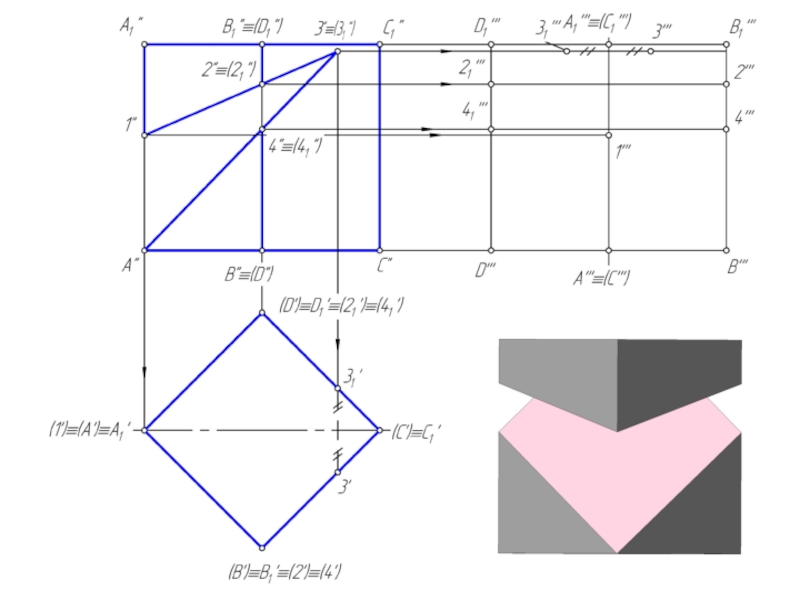
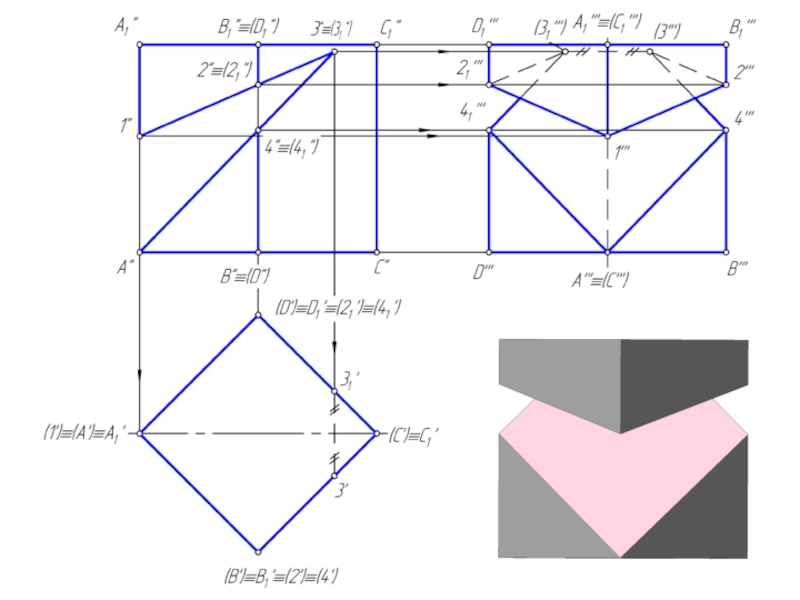
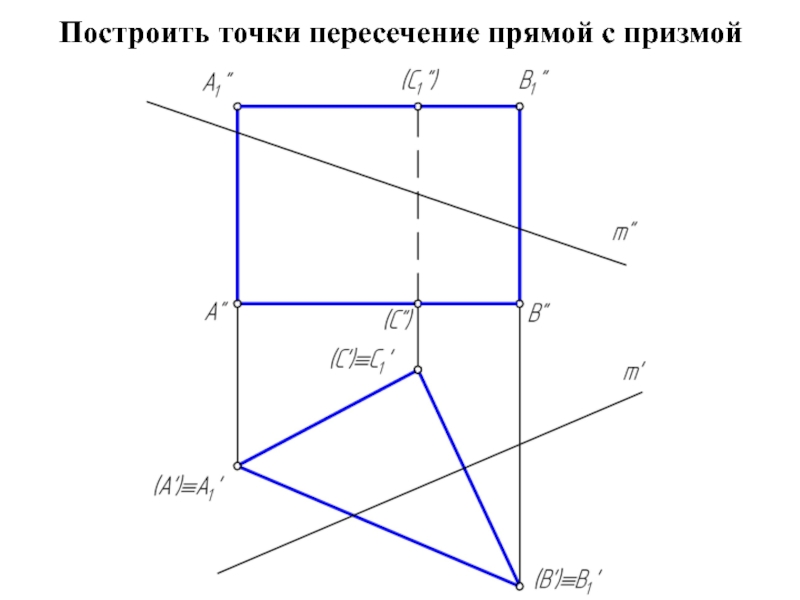
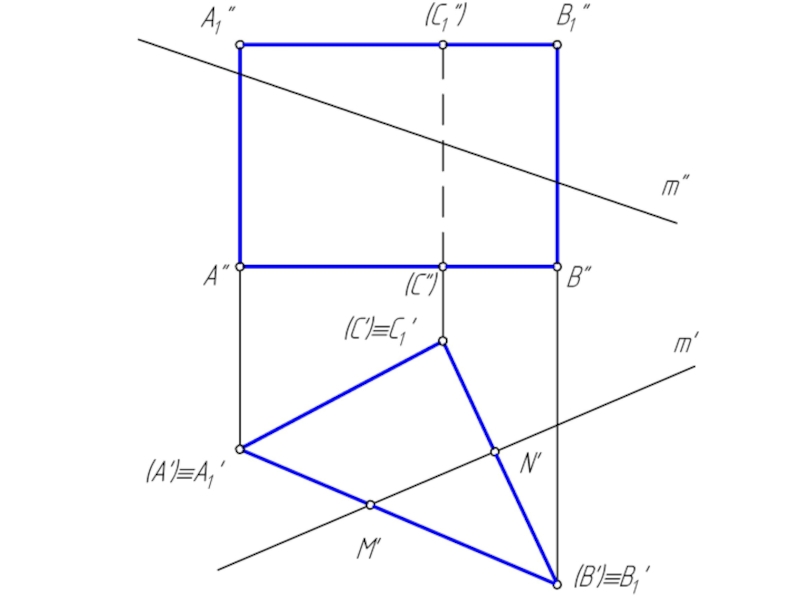
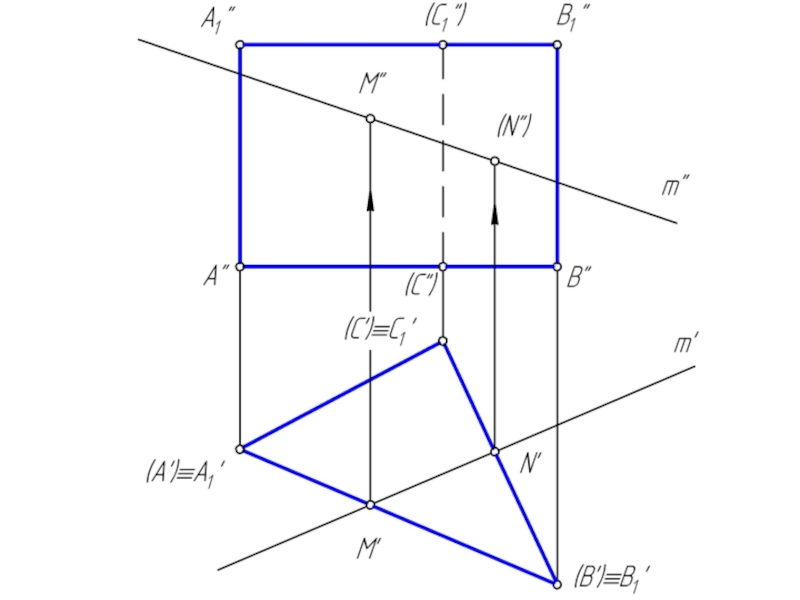
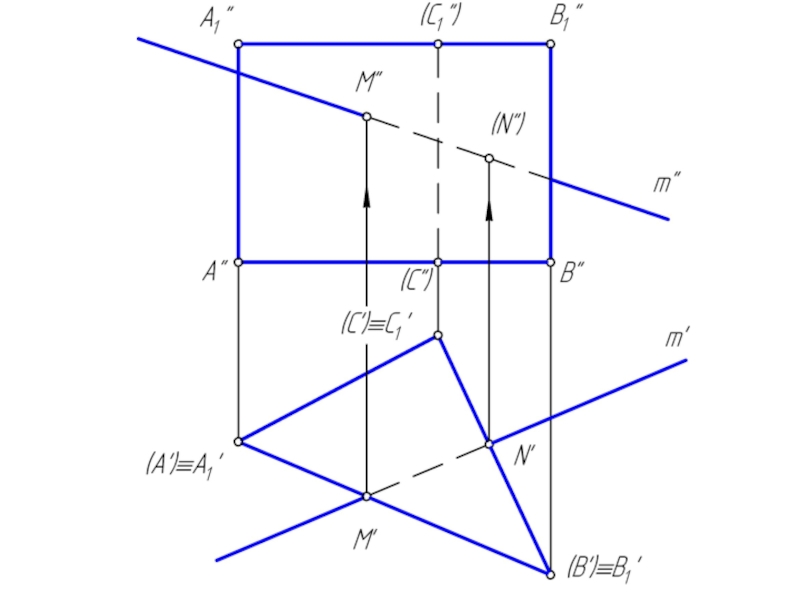
Сечением многогранника плоскостью является плоский многоугольник, вершины которого принадлежат ребрам, а стороны – граням многогранника.

лежащими в параллельных плоскостях, а остальные грани – параллелограммами (прямоугольниками),

имеющими общие стороны с этими многоугольниками.
Прямая призма – боковые ребра перпендикулярны основанию.
Наклонная призма – боковые ребра расположены под произвольным углом к основанию.
Правильная призма – в основании призмы лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.

необходимо найти:
1. точки, в которых ребра призмы пересекают

данную плоскость;
2. отрезки прямых, по которым грани призмы пересекаются заданной плоскостью.

значительно упрощается, если призма прямая и основание призмы параллельно плоскости

проекции.

В этом случае боковые грани призмы занимают проецирующее положение в пространстве.

Исходя из свойства проецирующих плоскостей, проекции точек пересечения прямой с поверхностью призмы принадлежат проецирующему следу плоскости (боковой грани призмы).