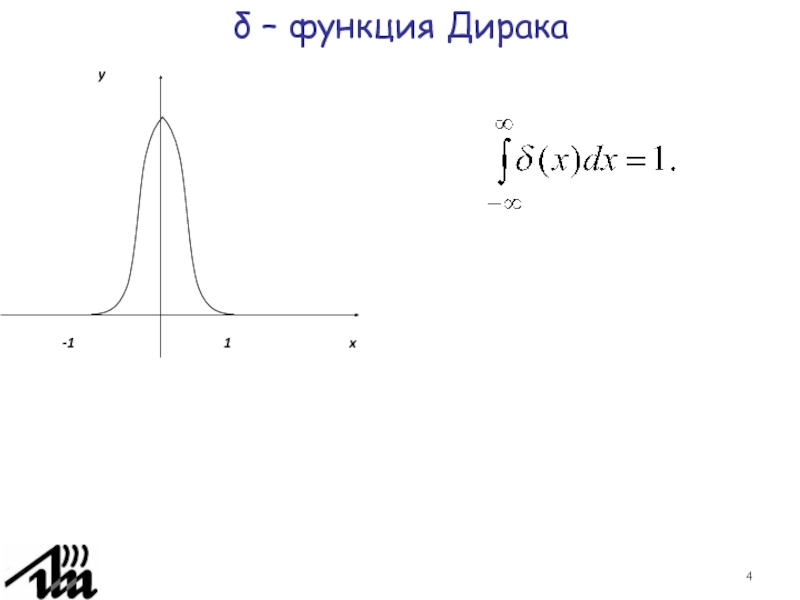
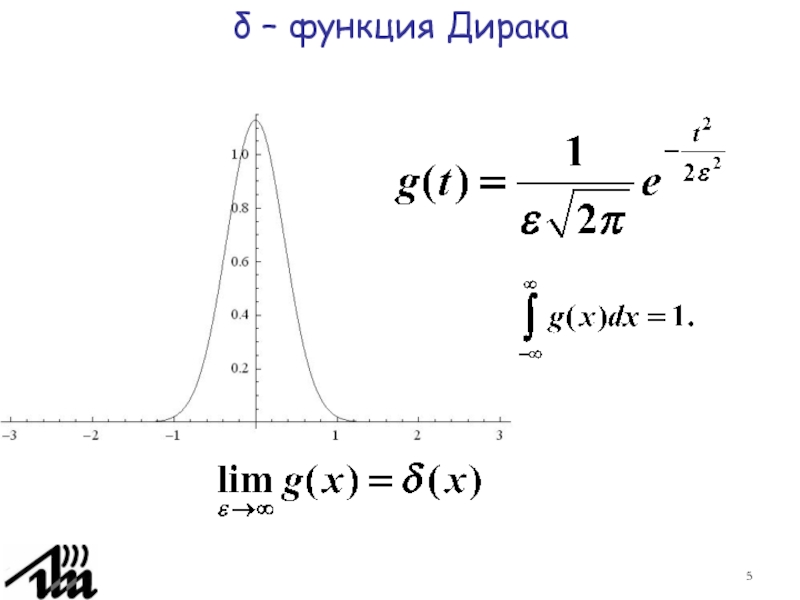
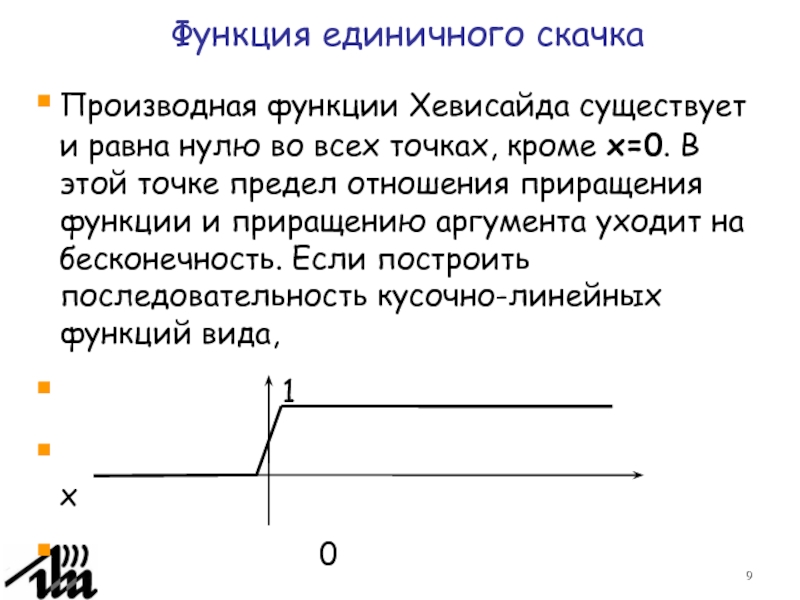
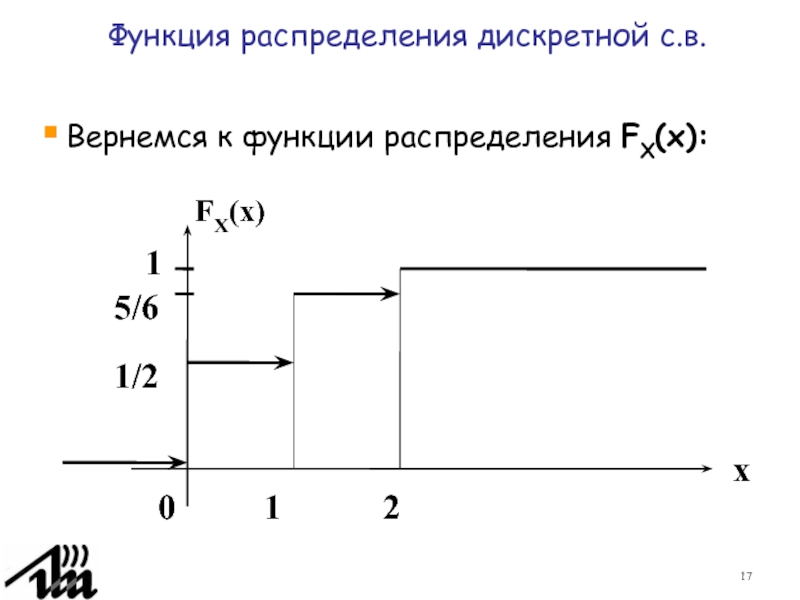
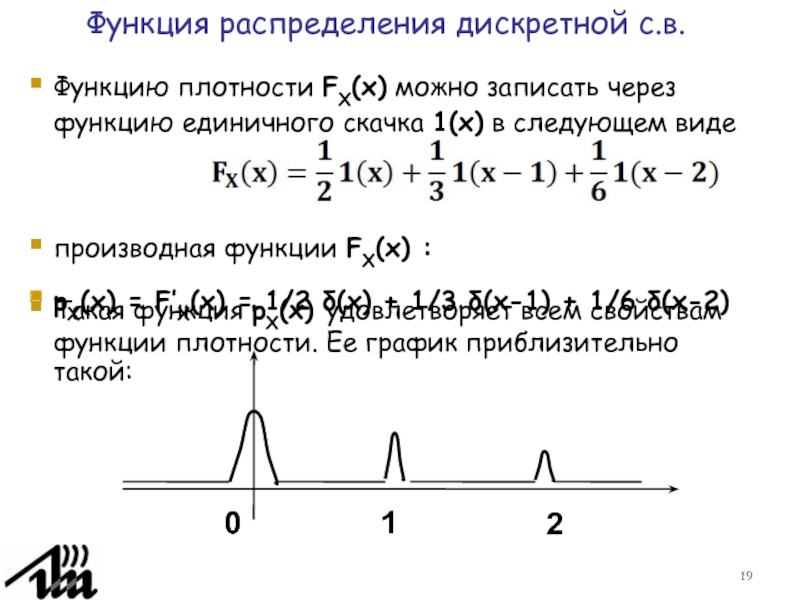
Функция распределения дискретной случайной величины.
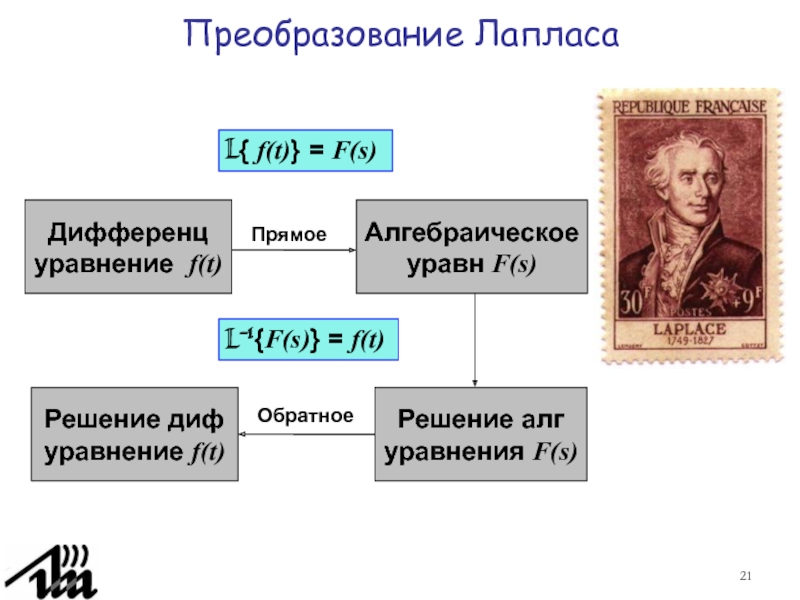
3.4. Преобразование Лапласа.
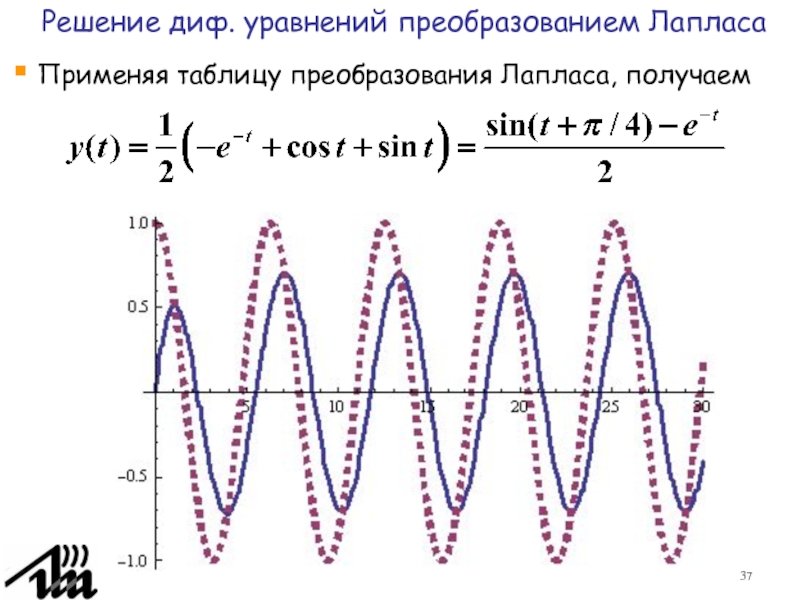
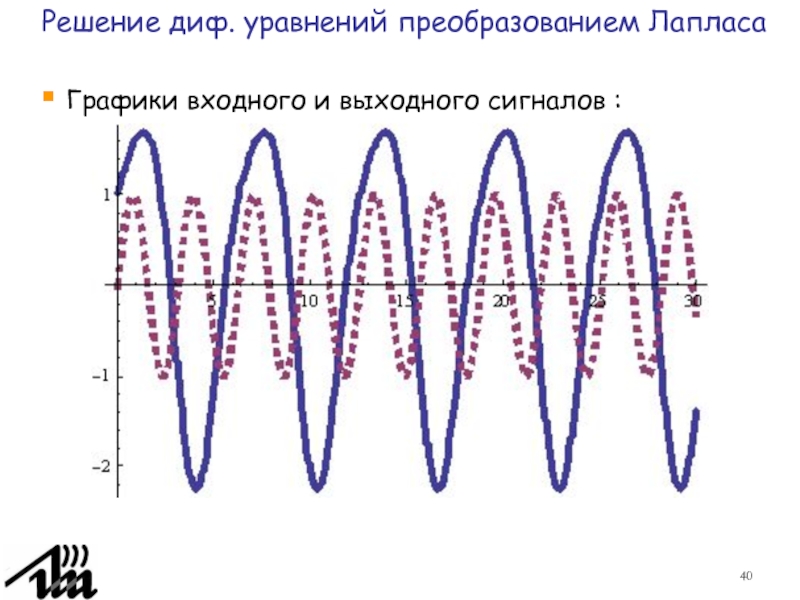
3.5. Решение диф. уравнений
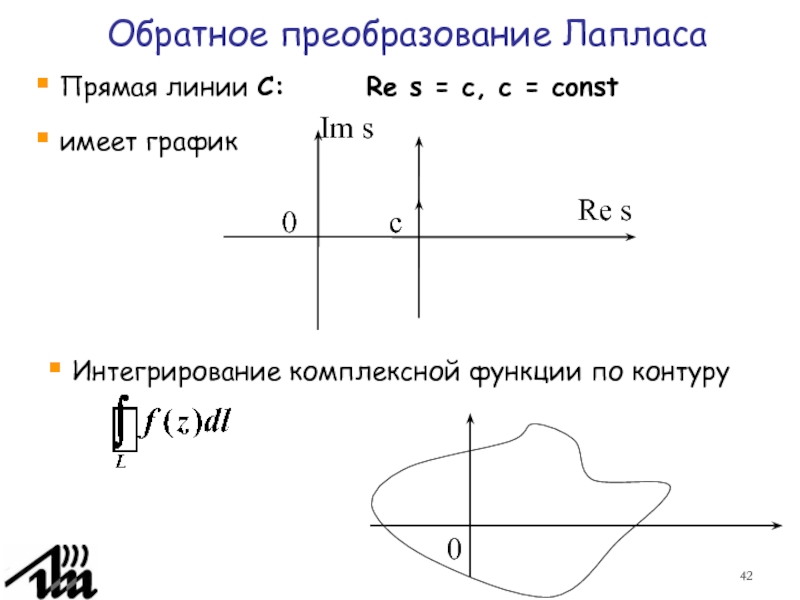
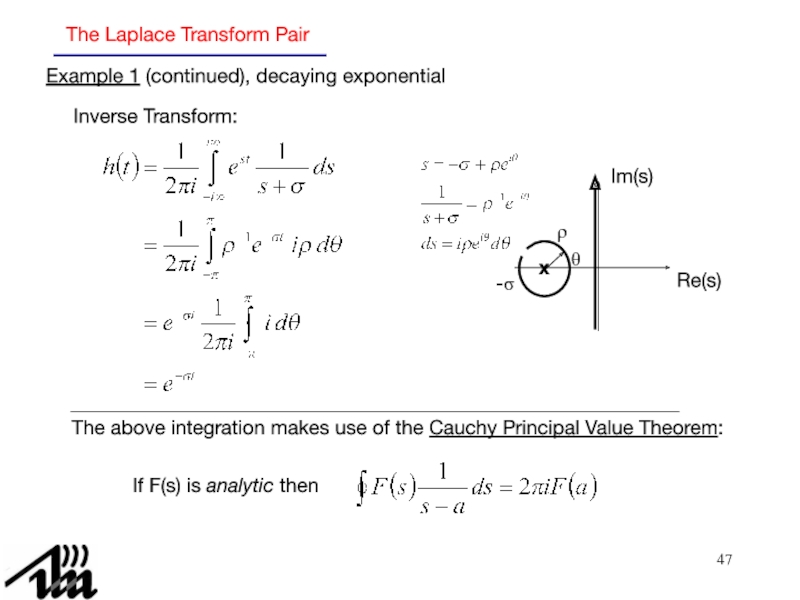
преобразованием Лапласа.3.6. Обратное преобразование Лапласа.
3.7. z-преобразование.