Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кинематика
Содержание
- 1. Кинематика
- 2. Программа по физике1 семестр1. Механика.2. Электричество и
- 3. Контрольное задание №1 1 семестр Участкин В.И., Никитин Б.И. ФИЗИКА: теория, контрольные задания и примеры решения задач, методические указания
- 4. ЛитератураСавельев И.В. Курс общей физики, т.1. Механика
- 5. Лекция 1 КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО
- 6. Материя. Пространство. Время.Материя - это окружающие нас
- 7. Механическое движениеОсновное свойство материи - материя всегда
- 8. Основные свойства пространства Пространство непрерывно.Пространство Эвклидово
- 9. Основные свойства времени Время непрерывно.
- 10. Физические модели в механикеМатериальная точка (МТ) -
- 11. Степени свободыЧислом степенями свободы механической системы называется
- 12. Поступательное движениеПоступательное движение – это движение, при
- 13. Системы отсчета.Система координат, служащая для указания положения
- 14. Декартова система координатyxzАi, j, k единичные вектора
- 15. Уравнение движения Одному векторному уравнению
- 16. Средняя скорость Путь s -длина траектории, пройденная
- 17. Линейная скорость Понятие мгновенной скорости относится к данной
- 18. Линейная скоростьРазложение скорости по ортам имеет видвеличина скорости v = ⎢v ⎢=
- 19. Линейное ускорение Вектор ускорения w определяет скорость
- 20. Определение путиПуть, пройденный материальной точкой за промежуток
- 21. Криволинейное движение Тангенциальное ускорение характеризует изменение скорости по
- 22. Полное ускорение Ускорение материальной точки, движущейся по произвольной
- 23. Поступательное движение АТТПри поступательном движении АТТ все
- 24. Вращательное движение В случае простого вращательного движения все
- 25. Вращательное движение При вращательном движении АТТ вводятся
- 26. Параметры вращательного движения Период обращения Т- время,
- 27. Кинематические параметры вращательного движения Вектор углового перемещения численно
- 28. Правило перемножения векторов Два типа перемножения :1)
- 29. Векторное произведение векторовАBα C =AB=[A B]=AB*sinα В
- 30. Угловая скорость. Связь линейной и угловой
- 31. Кинематика вращательного движения. модуль полного ускорения:Если ось
- 32. Сложное движениеПри сложном движении выделяют поступательное движение
- 33. Контрольные вопросы1. Назовите траекторию при которой радиус
- 34. Контрольные вопросы3. Камень брошен вблизи поверхности земли
- 35. Контрольные вопросы4. Диск радиусом 20 см вращается
- 36. Скачать презентанцию
Программа по физике1 семестр1. Механика.2. Электричество и магнетизм.3. Колебания 2 семестр4. Волны, оптика;5. Квантовая физика (включая физику атома и элементы физики твердого тела);6. Ядерная физика;7. Термодинамика и молекулярная физика (в том
Слайды и текст этой презентации
Слайд 1Лекции по физике
Ипполитова Галина Константиновна
доцент кафедры физики, к.ф.-м.н.
Кафедра физики ауд.
260,
Слайд 2Программа по физике
1 семестр
1. Механика.
2. Электричество и магнетизм.
3. Колебания
2
семестр
4. Волны, оптика;
5. Квантовая физика (включая физику атома и элементы
физики твердого тела);6. Ядерная физика;
7. Термодинамика и молекулярная физика
(в том числе элементы статистической физики).
8. Физическая картина мира.
Слайд 3Контрольное задание №1
1 семестр
Участкин В.И., Никитин Б.И.
ФИЗИКА:
теория, контрольные задания
и примеры решения задач,
методические указания
Слайд 4Литература
Савельев И.В. Курс общей физики, т.1. Механика - Спб.: Лань,
2011.
Савельев И.В. Курс общей физики, т.2. Электричество и магнетизм -
Спб.: Лань, 2011Трофимова Т. И. Курс физики: учеб. пособие для вузов. М. Издательский центр «Академия», 2010г.
Трофимова Т. И., А.В.Фирсов Курс физики. Задачи и решения, М. Издательский центр «Академия», 2010г.
Слайд 5
Лекция 1
КИНЕМАТИКА
ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ
Введение. Материя, пространство, время.
Модели в
механике. Системы отсчета.
Уравнения движения.
Кинематика поступательного движения.
Траектория, путь, скорость, ускорение.
Кинематика
вращательного движения.Угловые скорость и ускорение.
Слайд 6Материя. Пространство. Время.
Материя - это окружающие нас тела вместе с
создаваемыми ими полями.
Материя с точки зрения классической физики, существует в
двух видах:1) В виде вещества, состоящего из мельчайших частиц.
2) В виде поля (гравитационного,
электромагнитного).
Поле-это особый вид материи, передающий взаимодействие между телами.
Пространство и время – основные свойства существования материи.
Слайд 7Механическое движение
Основное свойство материи - материя всегда находится в непрерывном
движении.
В физике под движением понимают любое изменение состояния.
Простейшая форма
движения материи - механическое движение. Механическое движение- процесс изменения положения тела в пространстве с течение времени.
Слайд 8Основные свойства пространства
Пространство непрерывно.
Пространство Эвклидово или плоское.
Пространство трёхмерно.
Пространство однородно.
Пространственные соотношения инвариантны (неизменны) относительно параллельного переноса системы координат, нет
выделенных точек.5. Пространство изотропно. Пространственные соотношения инвариантны относительно вращения системы координат.
6. Для измерения пространственных объектов эталоном служит «линейка».
Слайд 9
Основные свойства времени
Время непрерывно.
Время одномерно, в отличие
от пространства.
Время однонаправлено.
Время однородно т.е. любые физические законы не
зависят от выбора начала отсчёта времени.Эталон для определения временных соотношений называется «часами».
Слайд 10Физические модели в механике
Материальная точка (МТ) - тело, размеры которого
в данной задаче можно пренебречь и считать, что все вещество
сосредоточено в точке.Абсолютно твердое тело (АТТ) - размеры тела неизменны, деформаций нет.
Сплошная среда - объект, в котором возможны деформации и перемещения; вещество тела распределено непрерывно
( жидкость, плазма)
Слайд 11Степени свободы
Числом степенями свободы механической системы называется число независимых величин
или число уравнений, полностью определяющих положение системы.
МТ имеет 3 степени
свободы Система из N материальных точек имеет
(3 N – К) степеней свободы, где К- число жестких связей.
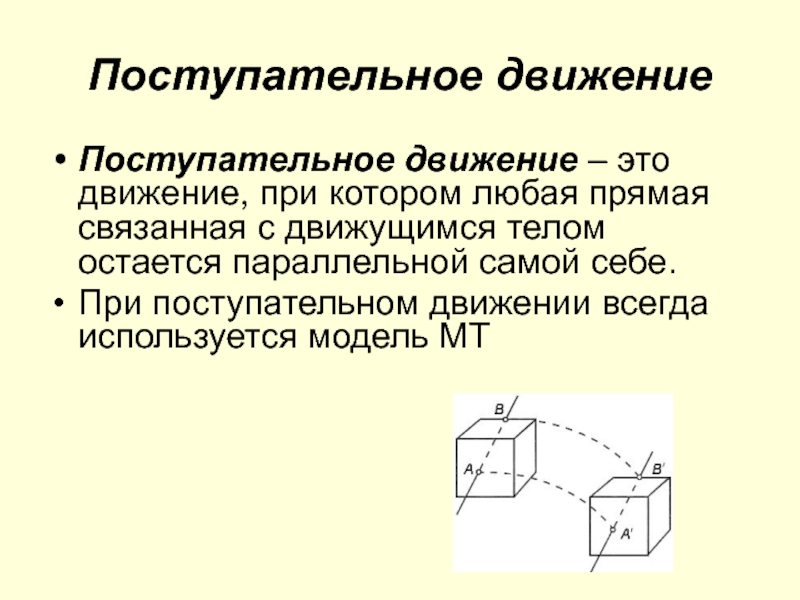
Слайд 12Поступательное движение
Поступательное движение – это движение, при котором любая прямая
связанная с движущимся телом остается параллельной самой себе.
При поступательном
движении всегда используется модель МТ
Слайд 13Системы отсчета.
Система координат, служащая для указания положения тела в пространстве,
вместе с часами для указания времени называется системой отсчета.
Система в
которой выполняется принцип инерции Галилея называется инерциальной системой отсчетаДекартова прямоугольная система координат - 3 взаимно перпендикулярных оси.
Положение МТ задается при помощи радиус-вектора R(t), проведенного из начала координат в данную точку.
МТ при своем движении описывает некую линию, которая называется траекторией.
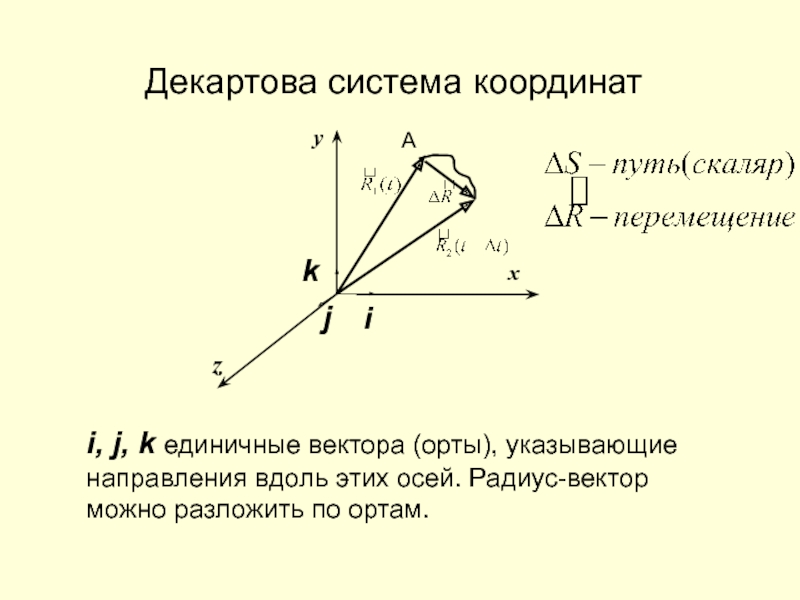
Слайд 14Декартова система координат
y
x
z
А
i, j, k единичные вектора (орты), указывающие направления
вдоль этих осей. Радиус-вектор можно разложить по ортам.
i
j
k
Слайд 15Уравнение движения
Одному векторному уравнению соответствуют три скалярных:
x = x(t); y = y(t); z
= z(t).x, y, z - проекции радиус-вектора на оси X,Y,Z соответственно.
Уравнение движения в координатной форме
Слайд 16Средняя скорость
Путь s -длина траектории, пройденная МТ
Средняя скорость -
отношение всего пройденного пути к соответствующему промежутку времени:
= s / t . При траекторном способе описания движения вводится бесконечно малый элемент траектории ds.
v =
V-скалярная величина, характеризующая быстроту изменения траектории по времени .
Слайд 17Линейная скорость
Понятие мгновенной скорости относится к данной точке и данному
моменту. Направлена мгновенная скорость по касательной в данной точке в
сторону движения.Если v = const, то есть скорость постоянна по величине и по направлению, то такое движение называется равномерным.
Слайд 19Линейное ускорение
Вектор ускорения w определяет скорость изменения вектора скорости
материальной точки со временем, равен производной от вектора скорости по
времени:
В зависимости от направления скорости и ускорения различают равноускоренное и равнозамедленное движения.
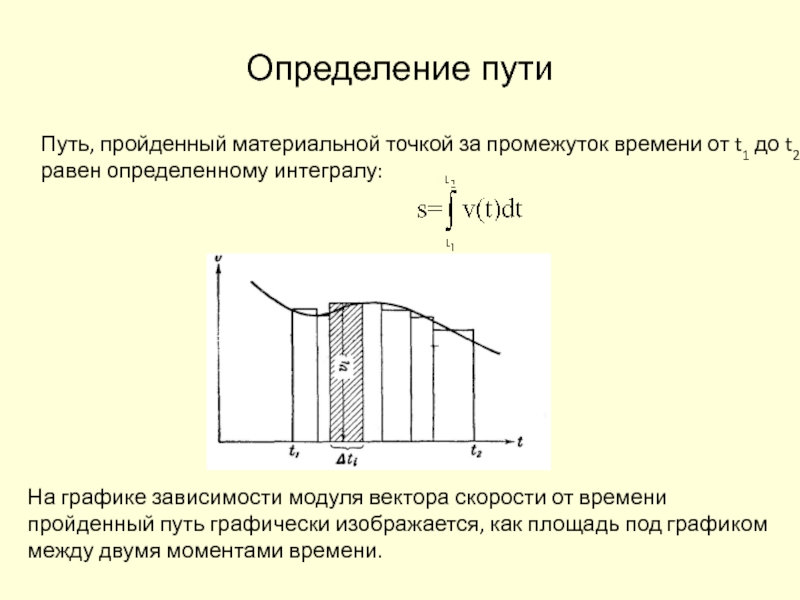
Слайд 20Определение пути
Путь, пройденный материальной точкой за промежуток времени от t1
до t2 равен определенному интегралу:
На графике зависимости модуля вектора скорости
от времени пройденный путь графически изображается, как площадь под графиком между двумя моментами времени.
Слайд 21Криволинейное движение
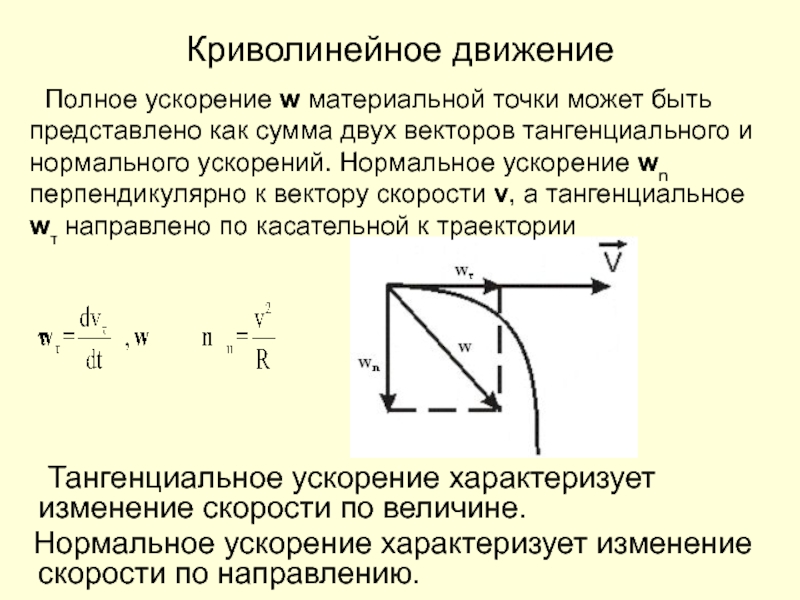
Тангенциальное ускорение характеризует изменение скорости по величине.
Нормальное ускорение характеризует изменение скорости по направлению.
Полное ускорение
w материальной точки может быть представлено как сумма двух векторов тангенциального и нормального ускорений. Нормальное ускорение wn перпендикулярно к вектору скорости v, а тангенциальное wτ направлено по касательной к траектории 
Слайд 22Полное ускорение
Ускорение материальной точки, движущейся по произвольной кривой зависит от
кривизны траектории, которая в разных точках может быть различна.
Модуль полного
ускорения
Слайд 23Поступательное движение АТТ
При поступательном движении АТТ все его точки перемещаются
по одинаковым траекториям и имеют одинаковые скорость и ускорение. Поэтому
при поступательном движении АТТ используются модель МТ и кинематические параметры для МТ.В этом случае выбирается одна точка, связанная с телом и описывается ее движение. Все остальные точки в движении отличаются только по координатам.
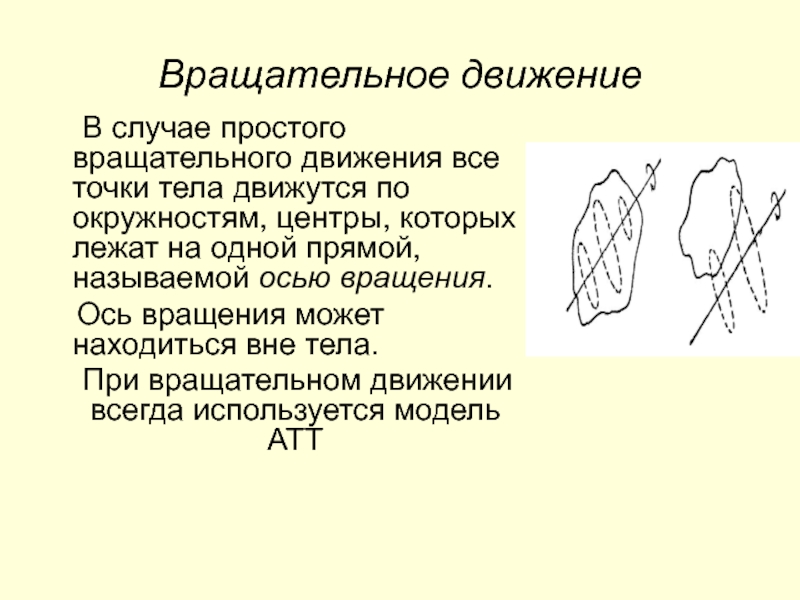
Слайд 24Вращательное движение
В случае простого вращательного движения все точки тела движутся
по окружностям, центры, которых лежат на одной прямой, называемой осью
вращения.Ось вращения может находиться вне тела.
При вращательном движении всегда используется модель АТТ
Слайд 25Вращательное движение
При вращательном движении АТТ вводятся угловые параметры, которые
являются одинаковыми для всех точек тела, поэтому они описывают движение
твердого тела как целого.Все вектора описывающие вращательное движение твердого тела являются аксиальными, т.е. направлены по оси вращения.
Слайд 26Параметры вращательного движения
Период обращения Т- время, за которое тело
делает один оборот, т.е. поворачивается на угол 2π
Частота- это
число оборотов в единицу времениЦиклическая частота:
измеряется в рад/с
Слайд 27Кинематические параметры вращательного движения
Вектор углового перемещения численно равен углу поворота
выраженного в радианах, а направление определяется по правилу правого винта.
ϕ=ϕ(t)
угловая
скорость ω = dϕ/dt угловое ускорение ε = dω/dt
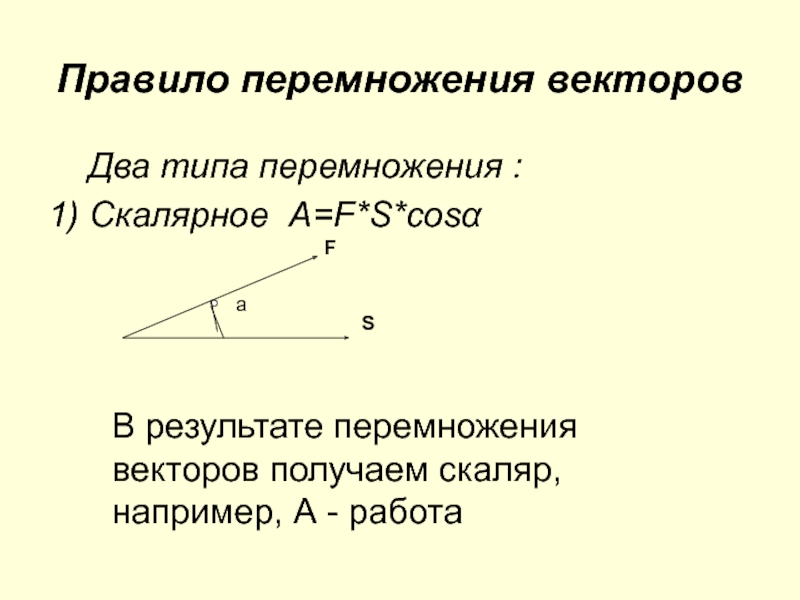
Слайд 28Правило перемножения векторов
Два типа перемножения :
1) Скалярное A=F*S*соsα
S
a
F
В результате
перемножения векторов получаем скаляр, например, А - работа
Слайд 29Векторное произведение векторов
А
B
α
C =AB=[A B]=AB*sinα
В результате векторного произведения
мы получаем вектор, модуль которого равен AB*sin α ,
а направление определяется по правилу правого винта. Результирующий вектор перпендикулярен плоскости в которой лежат перемножаемые вектора.
![Векторное произведение векторовАBα C =AB=[A B]=AB*sinα В результате векторного произведения мы получаем вектор, модуль которого равен](/img/tmb/2/143993/8bec5b51b9f7e6c3c41c10df6599ba7b-800x.jpg "Кинематика Векторное произведение векторовАBα C =AB=[A B]=AB*sinα В результате векторного произведения мы")
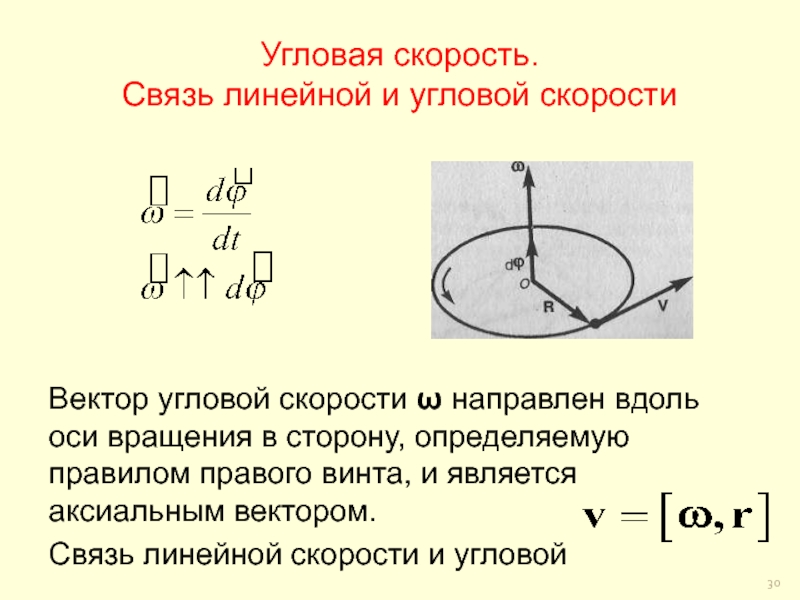
Слайд 30Угловая скорость.
Связь линейной и угловой скорости
Вектор угловой скорости ω
направлен вдоль оси вращения в сторону, определяемую правилом правого винта,
и является аксиальным вектором.Связь линейной скорости и угловой
Слайд 31Кинематика вращательного движения.
модуль полного ускорения:
Если ось вращения неподвижна,
то можно записать связь кинематических параметров поступательного и вращательного движения
в виде
:
Слайд 32Сложное движение
При сложном движении выделяют поступательное движение центра масс, а
дальше рассматривают вращение в системе центра масс.
В этом случае скорость
любой точки можно представить в виде Vi=Vc+[ω Ri′] (где R′ - радиус вектора в системе центра масс).
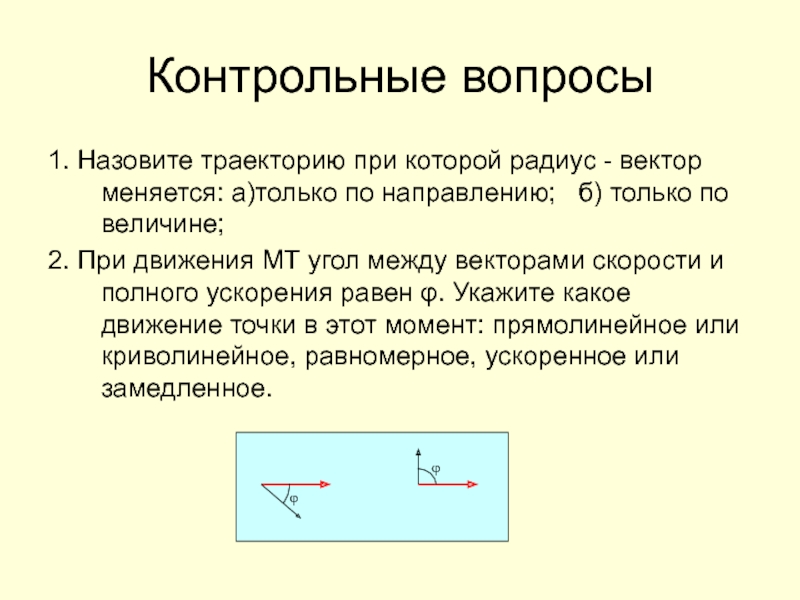
Слайд 33Контрольные вопросы
1. Назовите траекторию при которой радиус - вектор меняется:
а)только по направлению; б) только по величине;
2. При движения
МТ угол между векторами скорости и полного ускорения равен φ. Укажите какое движение точки в этот момент: прямолинейное или криволинейное, равномерное, ускоренное или замедленное.
Слайд 34Контрольные вопросы
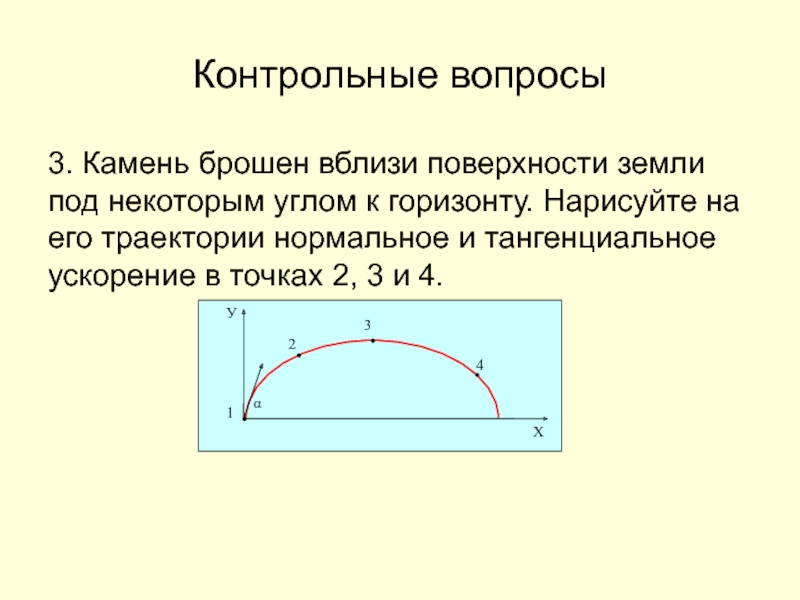
3. Камень брошен вблизи поверхности земли под некоторым углом
к горизонту. Нарисуйте на его траектории нормальное и тангенциальное ускорение
в точках 2, 3 и 4.
Слайд 35Контрольные вопросы
4. Диск радиусом 20 см вращается согласно уравнению
φ =
3 – t + 0,1t3 рад. Определить тангенциальное, нормальное и полное ускорения точек на окружности диска при t = 10 с.
