Логические функции

аргументы которой Х1, Х2 ..., Хn (независимые переменные) и сама

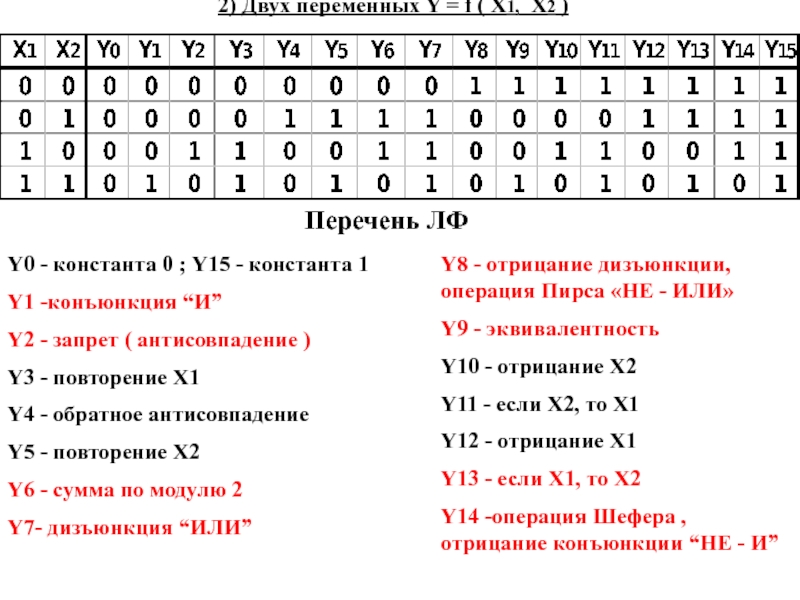
функция (зависимая переменная) принимают значения 0 или 1.
Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул.
Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности. Таблица истинности логической функции п аргументов содержит 2n строк, п столбцов значений аргументов и 1 столбец значений функции.
Одной переменной Y= f (X)

- константа 0 ; Y15 - константа 1
Y1 -конъюнкция “И”
Y2

- запрет ( антисовпадение )
Y3 - повторение X1
Y4 - обратное антисовпадение
Y5 - повторение X2
Y6 - сумма по модулю 2
Y7- дизъюнкция “ИЛИ”

Перечень ЛФ

Y8 - отрицание дизъюнкции, операция Пирса «НЕ - ИЛИ»
Y9 - эквивалентность
Y10 - отрицание X2
Y11 - если X2, то X1
Y12 - отрицание X1
Y13 - если X1, то X2
Y14 -операция Шефера , отрицание конъюнкции “НЕ - И”

то такая форма представления называется НОРМАЛЬНОЙ.
Элементарная конъюнкция — конъюнкция конечного

множества логических переменных и их инверсий.
Элементарная дизъюнкция — дизъюнкция конечного множества логических переменных и их инверсий.
Число аргументов, образующих элементарную дизъюнкцию или конъюнкцию, называется ее рангом.
Пример 1. Х1 *X2*X3 , Х1* X2* X3 — элементарные конъюнкции третьего ранга. X1+ X2, Х1+X2— элементарные дизъюнкции второго ранга.
Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции.
Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции, связанные между собой операцией конъюнкции.
Одну и ту же логическую функцию можно представить разными ДНФ и КНФ.
Для исключения неоднозначности записи логические функции могут быть представлены в совершенных дизъюнктивной и конъюнктивной нормальных формах.

двух одинаковых элементарных конъюнкций;
2) ни одна элементарная конъюнкция не

содержит двух одинаковых переменных;
3) ни одна элементарная конъюнкция не содержит переменную вместе с ее инверсией;
4) все конъюнкции имеют один и тот же ранг.
Аналогичным требованиям подчиняется и совершенная конъюнктивная нормальная форма (СКНФ).
Пример 2. Если логическая функция содержит конъюнкции разных рангов, то для получения СДНФ следует повысить ранг младших конъюнкций, используя закон исключения третьего(A+A=1).

F(X,Y,Z)= (X* Y) +(X*Y*Z) = (X*Y)* (Z+Z) +(X*Y*Z) =

=(X* Y* Z)+(X* Y*Z) + (X* Y* Z).

все наборы переменных, на которых функция принимает единичные значения.
2. Для

каждого выбранного набора записать элементарные конъюнкции, содержащие без инверсии переменные, принимающие в соответствующем наборе значение 1 и с инверсией — переменные, принимающие значение 0.
3. Соединить элементарные конъюнкции знаком дизъюнкции.

Алгоритм образования СКНФ по таблице истинности.
1. Выделить в таблице истинности все наборы переменных, на которых функция принимает нулевые значения.
2. Для каждого выбранного набора записать элементарные дизъюнкции. содержащие без инверсии переменные, принимающие в соответствующем наборе значение 0 и с инверсией — переменные, принимающие значение 1.
3. Соединить элементарные дизъюнкции знаком конъюнкции.

из трех) имеет три входные переменные (а, b, с), и

его выходная функция («функция большинства»)
F = 1, если, по крайней мере, две из входных переменных равны 1 (большинство, по-английски «majority»).
Мажоритарный элемент на 3 (и более) входов можно использовать как модель работы судейской коллегии (решение принимается по большинству голосов), если все судьи имеют равные права. Если же один из судей – старший, то необходимо закрепить его дополнительные права специальным соглашением.
Составьте электрические схемы мажоритарных элементов для различных случаев и в различных элементных базисах.