Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод Монте-Карло для решеточного газа Модель решеточного газа. Алгоритм Монте-Карло. Моделирование решеточного газа на двумерно
Содержание
- 1. Метод Монте-Карло для решеточного газа Модель решеточного газа. Алгоритм Монте-Карло. Моделирование решеточного газа на двумерно
- 2. Модель решеточного газаКаждому узлу простой кубической или
- 3. Модель решеточного газа на квадратной решеткеТочки соответствуют узлам решетки, занятым частицами
- 4. Модель решеточного газаМодельный гамильтониан, описывающий систему:Химический потенциал
- 5. Алгоритм Монте-КарлоГамильтониан диагонален в базисе чисел заполнения:Необходимо
- 6. Алгоритм Монте-КарлоПроцедуры рождения и уничтожения частиц: разные
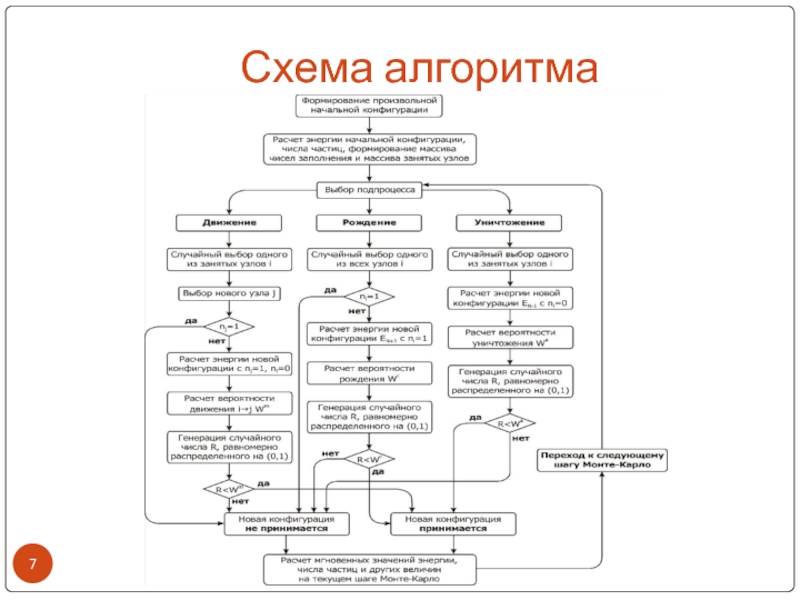
- 7. Схема алгоритма
- 8. Алгоритм Монте-КарлоЧисло шагов в алгоритме МК определяется
- 9. Моделирование решеточного газа на двумерной решеткеМоделирование решеточного
- 10. Моделирование решеточного газа на двумерной решеткеПри повышении
- 11. Скачать презентанцию
Модель решеточного газаКаждому узлу простой кубической или квадратной решетки ставится в соответствие число заполнения 0 или 1, моделирующее нахождение или отсутствие частицы в данном узле Полное число состояний в системе совпадает
Слайды и текст этой презентации
Слайд 1Модель решеточного газа. Алгоритм Монте-Карло. Моделирование решеточного газа на двумерной
решетке
Слайд 2Модель решеточного газа
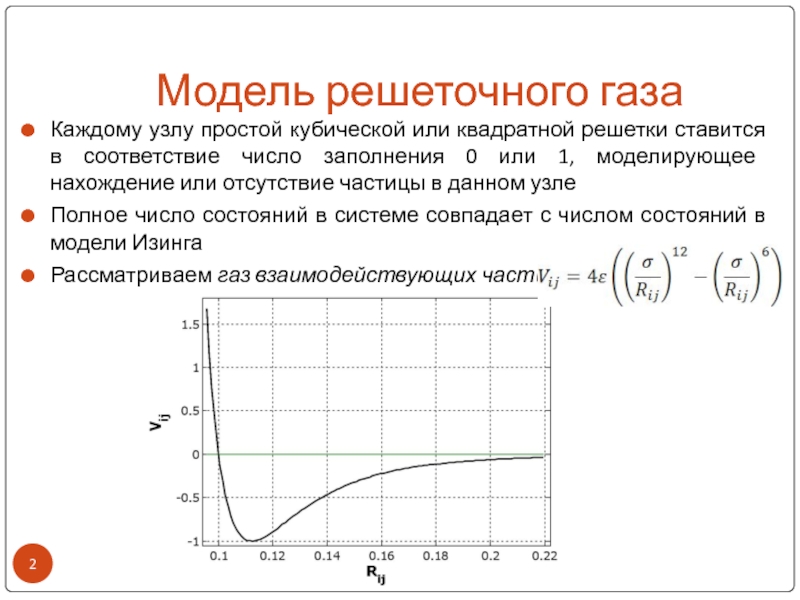
Каждому узлу простой кубической или квадратной решетки ставится
в соответствие число заполнения 0 или 1, моделирующее нахождение или
отсутствие частицы в данном узлеПолное число состояний в системе совпадает с числом состояний в модели Изинга
Рассматриваем газ взаимодействующих частиц
Слайд 3Модель решеточного газа
на квадратной решетке
Точки соответствуют узлам решетки, занятым частицами
Слайд 4Модель решеточного газа
Модельный гамильтониан, описывающий систему:
Химический потенциал отвечает переменному числу
частиц в системе и является функцией внешнего давления
Уравнение состояния:
Трикритическая точка:
Решеточная
модель описываетфазовый переход первого рода
"жидкость – газ"
Слайд 5Алгоритм Монте-Карло
Гамильтониан диагонален в базисе чисел заполнения:
Необходимо реализовать принцип детального
равновесия в условиях большого канонического ансамбля
Для эффективного перебора состояний системы
достаточно ввести два типа подпроцессов: движение частиц и рождение/уничтожение частицСоотношение детального баланса должно быть выполнено для каждой пары прямой и обратной процедур внутри одного типа подпроцессов, независимо от других типов подпроцессов
Уравнение детального баланса для подпроцессов движения со схемой Метрополиса:
Слайд 6Алгоритм Монте-Карло
Процедуры рождения и уничтожения частиц: разные вероятности обращения
Уравнение детального
баланса:
Возможный выбор вероятностей перехода:
Множитель τ является произвольным и дает дополнительную
степень свободы, его выбор позволяет оптимизировать обновление конфигураций
Слайд 8Алгоритм Монте-Карло
Число шагов в алгоритме МК определяется достижением необходимой сходимости
рассчитываемых величин
Для модели решеточного газа процедура МК позволяет при любом
виде межчастичного взаимодействия рассчитать фазовую диаграмму "жидкость – газ", и, в частности, построить изотермыПри заданной температуре и химическом потенциале рассчитывается среднее число частиц в системе, и, соответственно, плотность
Давление можно представить как функцию химического потенциала:
Слайд 9Моделирование решеточного газа
на двумерной решетке
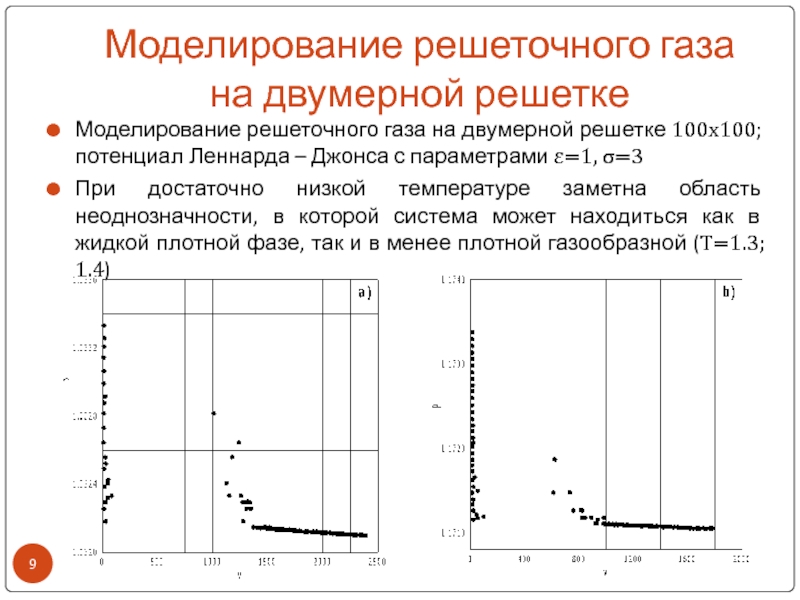
Моделирование решеточного газа на двумерной решетке
100х100; потенциал Леннарда – Джонса с параметрами ε=1, σ=3
При достаточно
низкой температуре заметна область неоднозначности, в которой система может находиться как в жидкой плотной фазе, так и в менее плотной газообразной (T=1.3; 1.4)
Слайд 10Моделирование решеточного газа
на двумерной решетке
При повышении температуры область неоднозначности заметно
сжимается и затем при более высоких температурах исчезает, так что
система все время остается в газообразной фазе (T=1.45; 1.55)Значение температуры в трикритической точке можно оценить как