Динамика систем с конечным числом степеней свободы масс

условно недеформированное ) состояние





В произвольный
момент движения
( t )


J1 (t)
Jk

(t)

F (t)

M (t)

q (t)

Δc (t)

y1 (t)

y2 (t)

yi (t)

yk (t)

yn (t)

yn-1 (t)

J2 (t)

Ji (t)

Jn (t)

Jn-1 (t)

По принципу
Д’Аламбера

Компоненты
динамических
механических
воздействий

Pp(t) = Pp * ψp (t)

0

t

Pp(t)

Pp

FD,n (t)

FD,i (t)

FD,1 (t)

FD,2 (t)

от силовых
воздействий

от кинематических
воздействий

δik – перемещение по
направлению Ji от Jk = 1

Δip – перемещение по
направлению Ji от Pp

δik – перемещение по
направлению Ji от Jk = 1

ψp(t)

1

Pp * ψp (t)

0
t

Δip – перемещение по
направлению Ji от

Pp

δik – перемещение по
направлению Ji от Jk = 1

В произвольный
момент движения
( t )

J1 (t)

Jk (t)

F (t)

M (t)

q (t)

Δc (t)

J2 (t)

Ji (t)

Jn (t)

Jn-1 (t)

По принципу
Д’Аламбера

ψp(t)

1

По закону инерции:

По модели Фойгта:

Дифференциальные уравнения вынужденного движения
системы с конечным числом степеней свободы масс

y1 (t)

y2 (t)

yi (t)

yk (t)

yn (t)

yn-1 (t)

FD,n (t)

FD,i (t)

FD,1 (t)

FD,2 (t)

момент движения
( t )
J1 (t)
Jk (t)
F (t)
M (t)
q (t)
Δc (t)


J2

(t)

Ji (t)

Jn (t)

Jn-1 (t)

По принципу
Д’Аламбера

Компоненты
динамических
механических
воздействий

0

t

Δip – перемещение по
направлению Ji от Pp

δik – перемещение по
направлению Ji от Jk = 1

Pp(t) = Pp * ψp (t)

ψp(t)

1

Дифференциальные уравнения вынужденного движения
системы с конечным числом степеней свободы масс

Случай вибрационных
( гармонических ) воздействий,
синфазных, моногармонических

0

t

= sin ωF t

Рабочие
гипотезы:

2. Сопротивление движению считается
пренебрежимо малым; разность фаз
воздействий и перемещений
масс принимается равной 0.

1. Рассматриваются
установившиеся
вынужденные
колебания с частотой ωF .

y1 (t)

y2 (t)

yi (t)

yk (t)

yn (t)

yn-1 (t)

FD,n (t)

FD,i (t)

FD,1 (t)

FD,2 (t)

момент движения
( t )
J1 (t)
Jk (t)
F (t)
M (t)
q (t)
Δc (t)
y1

(t)

y2 (t)

yi (t)

yk (t)

yn (t)

yn-1 (t)

J2 (t)

Ji (t)

Jn (t)

Jn-1 (t)

Компоненты
динамических
механических
воздействий

FD,n (t)

FD,i (t)

FD,1 (t)

FD,2 (t)

Δip – перемещение по
направлению Ji от Pp

δik – перемещение по
направлению Ji от Jk = 1

Pp(t) = Pp * ψp (t)

ψp(t)

Дифференциальные уравнения вынужденного движения
системы с конечным числом степеней свободы масс

Случай вибрационных
( гармонических ) воздействий,
синфазных, моногармонических

0

t

= sin ωF t

Рабочие
гипотезы:

2. Сопротивление движению считается
пренебрежимо малым; разность фаз
воздействий и перемещений
масс принимается равной 0.

yk(t) = yk sin ωF t , k = 1,…,n

yi(t) = yi sin ωF t

Уравнения установившихся вынужденных колебаний
системы с конечным числом степеней свободы масс

1. Рассматриваются
установившиеся
вынужденные
колебания с частотой ωF .

момент движения
( t )
J1 (t)
Jk (t)
F (t)
M (t)
q (t)
Δc (t)
y1

(t)

y2 (t)

yi (t)

yk (t)

yn (t)

yn-1 (t)

J2 (t)

Ji (t)

Jn (t)

Jn-1 (t)

Компоненты
динамических
механических
воздействий

Δip – перемещение по
направлению Ji от Pp

δik – перемещение по
направлению Ji от Jk = 1

Pp(t) = Pp* ψp (t)

ψp(t)

Случай вибрационных
( гармонических ) воздействий,
синфазных, моногармонических

0

t

= sin ωF t

Рабочие
гипотезы:

2. Сопротивление движению считается
пренебрежимо малым; разность фаз
воздействий и перемещений
масс принимается равной 0.

yk(t) = yk sin ωF t , k = 1,…,n

Уравнения установившихся вынужденных колебаний
системы с конечным числом степеней свободы масс

( в амплитудах перемещений масс )

J1

Jk

J2

y1

y2

yk

В амплитудном
состоянии

M

F

q

Ji

yi

yn

yn-1

Jn

Jn-1

Δc

1. Рассматриваются
установившиеся
вынужденные
колебания с частотой ωF .

перемещение по
направлению Ji от Pp
δik – перемещение

по
направлению Ji от Jk = 1

Pp(t) = Pp * ψp (t)

ψp(t)

Случай вибрационных
( гармонических ) воздействий,
синфазных, моногармонических

0

t

= sin ωF t

Рабочие
гипотезы:

2. Сопротивление движению считается
пренебрежимо малым; разность фаз
воздействий и перемещений
масс принимается равной 0.

yk(t) = yk sin ωF t , k = 1,…,n

Уравнения установившихся вынужденных колебаний
системы с конечным числом степеней свободы масс

ΔiΣ – перемещение по на-правлению Ji от амплитуд
Pp заданных воздействий

( в амплитудах перемещений масс )

( в амплитудах инерционных cиловых факторов )

В амплитудном
состоянии

J1

Jk

J2

y1

y2

yk

M

F

q

Ji

yi

yn

yn-1

Jn

Jn-1

Δc

1. Рассматриваются
установившиеся
вынужденные
колебания с частотой ωF .

перемещение по на-правлению Ji от амплитуд
Pp заданных воздействий
δik

– перемещение по
направлению Ji от Jk = 1

Pp(t) = Pp * ψp (t)

ψp(t)

Случай вибрационных
( гармонических ) воздействий,
синфазных, моногармонических

0

t

= sin ωF t

Рабочие
гипотезы:

1. Рассматриваются
установившиеся
вынужденные
колебания с частотой ωF .

2. Сопротивление движению считается
пренебрежимо малым; разность фаз
воздействий и перемещений
масс принимается равной 0.

yk(t) = yk sin ωF t , k = 1,…,n

Уравнения установившихся вынужденных колебаний
системы с конечным числом степеней свободы масс

( в амплитудах инерционных cиловых факторов )

В амплитудном
состоянии

J1

Jk

J2

y1

y2

yk

M

F

Ji

yi

q

yn

yn-1

Jn

Jn-1

Δc

колебаний (УВК)
Системы с конечным числом n при вибрационных воздействиях,

в

амплитудах инерционных силовых факторов ( сил инерции ):

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

В матричной форме:

колебаний (УВК)
Системы с конечным числом n при вибрационных воздействиях,

вектор
амплитуд
инерционных

сил

– матрица динамической
податливости системы
по направлениям
инерционных сил

δ – матрица
упругой податливости системы по направлениям
инерционных сил

матрица динамических ( инерционных ) поправок к податливости системы

матрица обобщённых (при-ведённых) характеристик масс, порождающих инерци-онные силовые факторы
J1 , J2 ,…, Jn

Решение системы
уравнений УВК:

условие существования
единственного решения

В матричной форме:

в амплитудах инерционных силовых факторов ( сил инерции ):

вектор перемеще-
ний от амплитуд
воздействий

установившихся вынужденных колебаниях системы с конечным числом n при вибрационных

воздействиях

Sdyn(t) = Sdyn sin ωF t

0

t

Sdyn

от амплитуд
сил инерции

от амплитуд
заданных
воздействий

от
Jk = 1

F1

F2

J1

J2

Mdyn

– Mdyn

Mdyn, max

MF – для сравнения

Проверка результатов
динамического расчета
на вибрационные воздействия

1. Статическая проверка – проверка равнове-
сия системы и её частей при действии задан-
ных нагрузок и добавленных сил инерции масс.

2. Кинематическая проверка ( главная ) – проверка
амплитуд динамических перемещений масс:

установившихся вынужденных колебаниях системы с конечным числом n при вибрационных

воздействиях

Sdyn(t) = Sdyn sin ωF t

0

t

Sdyn

от амплитуд
сил инерции

от амплитуд
заданных
воздействий

от
Jk = 1

F1

F2

J1

J2

Mdyn

– Mdyn

Mdyn, max

MF – для сравнения

Динамические коэффициенты

Динамический коэффициент –
отношение наибольшего значения величины Р
( некоторого параметра НДС ) от динамического воздействия к её значению при условном статическом приложении амплитуд
заданных воздействий.

Динамические коэффициенты

μΔ = | Δdyn |/| ΔΣ |

μS = | Sdyn |/| SΣ |

по перемещениям

по усилиям

установившихся вынужденных колебаниях системы с конечным числом n при вибрационных

воздействиях

J1(1)

J2

MF

П р и м е р

m

2m

3m

F(t)

2

2

6 м

3

2EI

EI

EI

m

2m

3m

J1(2)

J1(3)

F(t) = F sin ωF t , ωF = 0,8 ωmin

n = 2

J1 = J1(1) + J1(2) + J1(3)

J1 = 1

k = 1

МС

J2 = 1

k = 2

МС

F

МС

F

2

2

2

2

3

2,206

0,794

M1

M2

( x F )

1,176

1,412

0,824

установившихся вынужденных колебаниях системы с конечным числом n при вибрационных

воздействиях

J1(1)

J2

MF

П р и м е р

m

2m

3m

F(t)

2

2

6 м

3

2EI

EI

EI

m

2m

3m

J1(2)

J1(3)

F(t) = F sin ωF t , ωF = 0,8 ωmin

J1 = 1

k = 1

МС

J2 = 1

k = 2

МС

F

МС

F

2

2

2

2

3

2,206

0,794

M1

M2

( x F )

1,176

1,412

0,824

– из уравнения частот СК:

J1 = 1,092 F ; J2 = 0,146 F

установившихся вынужденных колебаниях системы с конечным числом n при вибрационных

воздействиях

J1(1)

J2

MF

П р и м е р

m

2m

3m

F(t)

2

2

6 м

3

2EI

EI

EI

m

2m

3m

J1(2)

J1(3)

F(t) = F sin ωF t , ωF = 0,8 ωmin

J1 = 1

k = 1

МС

J2 = 1

k = 2

МС

F

МС

F

2

2

2

2

3

2,206

0,794

M1

M2

( x F )

1,176

1,412

0,824

J1 = 1,092 F ; J2 = 0,146 F

Mdyn = M1J1 + M2J2 + MF

0,436

3,682

3,123

3,123

2,562

Mdyn

( x F )

3,245

установившихся вынужденных колебаниях системы с конечным числом n при вибрационных

воздействиях

J1(1)

J2

MF

П р и м е р

m

2m

3m

F(t)

2

2

6 м

3

2EI

EI

EI

m

2m

3m

J1(2)

J1(3)

F(t) = F sin ωF t , ωF = 0,8 ωmin

J1 = 1

k = 1

МС

J2 = 1

k = 2

МС

F

МС

F

2

2

2

2

3

2,206

0,794

M1

M2

( x F )

1,176

1,412

0,824

Mdyn = M1J1 + M2J2 + MF

0,436

3,682

3,123

3,123

2,562

Mdyn

( x F )

3,245

Динамические коэффициенты:

по перемещениям

по моментам

с конечным числом степеней свободы масс

0
ωF
Расчётные усилия при динамических воздействиях
При

совпадении частоты воздействий ωF
с любой собственной частотой ( ωF = ωj ):

yi

ΔiΣ

ω1

ωj

ωn

ω2

….

….

Условие недопущения резонанса:

kω > 1 – коэффициент надёжности по частоте

0

t

|Sdyn|

Smax

Sconst

|Sdyn|

|Sdyn|

ΣStemp, min< 0

ΣStemp, max > 0

Smin

S(t)

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

1

2

3

4

5

1

2

3

4

5

Расчётные
узлы

ОСМП

F

q

Δc

1

2

3

4

5

ОСМП

F

q

Δc

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

Основные
неизвестные:

компоненты
перемещений
масс (степени
свободы)

дополнительные
перемещения
расчётных узлов

nZ = nθ + nΔ = n + nd

yk = Zk

Z1 = y1

J1

Ji

Jk

yi = Zi

1

2

3

4

5

ОСМП

F

q

Δc

q,F, Δc – амплитуды
заданных воздействий

Ri

Rk

R1

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

Основные
неизвестные:

компоненты
перемещений
масс (степени
свободы)

дополнительные
перемещения
расчётных узлов

nZ = nθ + nΔ = n + nd

yk = Zk

Z1 = y1

J1

Ji

Jk

yi = Zi

1

2

3

4

5

ОСМП

F

q

Δc

q,F, Δc – амплитуды
заданных воздействий

Ri

Rk

R1

Полная реакция
i-ой связи:
Ri = 0,
Ri = RiZ + RiJ + RiΣ

От перемещений узлов Z:

От cил инерции J: RiJ = – Ji

К У М П

i = 1, 2,…, nZ

К У М П

i = 1, 2,…, n

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

Основные
неизвестные:

компоненты
перемещений
масс (степени
свободы)

дополнительные
перемещения
расчётных узлов

nZ = nθ + nΔ = n + nd

1

2

3

4

5

ОСМП

F

q

Δc

q,F, Δc – амплитуды
заданных воздействий

К У М П

i = 1, 2,…, n

i = n + 1, …, n + nd

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

1

2

3

4

5

ОСМП

F

q

Δc

q,F, Δc – амплитуды
заданных воздействий

К У М П

i = 1, 2,…, n

i = 1, 2,…, n

матрица динамической
жёсткости ОСМП

nd

Zm = y

i = n + 1, …, n + nd

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

1

2

3

4

5

ОСМП

F

q

Δc

q,F, Δc – амплитуды
заданных воздействий

К У М П

i = 1, 2,…, n

матрица динамической
жёсткости ОСМП

nd

Zm = y

Исключение дополнительных перемещений Zd :

Уравнения МП для основной системы
со связями только по направлениям
перемещений масс:

Основные неизвестные:

i = n + 1, …, n + nd

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

1

2

3

4

5

ОСМП

F

q

Δc

q,F, Δc – амплитуды
заданных воздействий

К У М П

i = 1, 2,…, n

матрица динамической
жёсткости ОСМП

Zm = y

Исключение дополнительных перемещений Zd :

Уравнения МП для основной системы
со связями только по направлениям
перемещений масс:

Основные неизвестные:

Амплитуды
динамических усилий:

Случай
собственных колебаний

i = n + 1, …, n + nd

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

1

2

3

4

5

ОСМП

К У М П

i = 1, 2,…, n

матрица динамической
жёсткости ОСМП

Zm = y

Исключение дополнительных перемещений Zd :

Уравнения МП для основной системы
со связями только по направлениям
перемещений масс:

Основные неизвестные:

Амплитуды
динамических усилий:

Случай
собственных колебаний

i = n + 1, …, n + nd

метода перемещений
в динамических расчётах при гармонических колебаниях
Специальное требование

к формированию основной системы МП:
расчётные узлы назначаются в местах расположения масс,
а также по правилам, принятым в статических расчётах по МП.

1

2

3

4

5

ОСМП

i = 1, 2,…, n

матрица динамической
жёсткости ОСМП

Zm = y

Исключение дополнительных перемещений Zd :

Основные неизвестные:

Случай
собственных колебаний

i = 1, 2,…, n

i = n + 1, …, n + nd

К У М П

Уравнение частот собственных колебаний:

nd

Уравнения МП для основной системы
со связями только по направлениям
перемещений масс:

i = n + 1, …, n + nd

учёт симметрии в динамических расчётах
Переход от исходных неизвестных J
к новым

( групповым ) неизвестным :

– матрица линейного
преобразования
неизвестных

Новые ( групповые ) неизвестные

. . . . . . . . . . . . . . .

J1

J2

Jk

Jn

y1

y2

yk

yn

Исходные неизвестные
( инерционные силовые факторы )

Обобщённые перемещения , соответствующие групповым неизвестным :

Из условия

учёт симметрии в динамических расчётах
Переход от исходных неизвестных J
к новым

( групповым ) неизвестным :

– матрица линейного
преобразования
неизвестных

Новые ( групповые ) неизвестные

. . . . . . . . . . . . . . .

J1

J2

Jk

Jn

Исходные неизвестные
( инерционные силовые факторы )

Обобщённые перемещения , соответствующие групповым неизвестным :

Из условия

Приведённые массы , соответству-
ющие групповым неизвестным :

Из условия

y1

y2

yk

yn

учёт симметрии в динамических расчётах
Переход от исходных неизвестных J
к новым

( групповым ) неизвестным :

– матрица линейного
преобразования
неизвестных

Новые ( групповые ) неизвестные

. . . . . . . . . . . . . . .

Исходные неизвестные
для симметричной системы

Обобщённые перемещения , соответствующие групповым неизвестным :

Приведённые массы , соответству-
ющие групповым неизвестным :

Ji

Jk

yi

yk

С

a

a

учёт симметрии в динамических расчётах
Переход от исходных неизвестных J
к новым

( групповым ) неизвестным :

– матрица линейного
преобразования
неизвестных

Новые ( групповые ) неизвестные

Ji

yi

yk

Исходные неизвестные
для симметричной системы

Обобщённые перемещения , соответствующие групповым неизвестным :

Приведённые массы , соответству-
ющие групповым неизвестным :

С

a

a

С

a

a

yi

yk

– симметрич.

– обратносим.

Jk

учёт симметрии в динамических расчётах
Переход от исходных неизвестных J
к новым

( групповым ) неизвестным :

– матрица линейного
преобразования
неизвестных

Новые ( групповые ) неизвестные

Ji

yi

yk

Исходные неизвестные
для симметричной системы

Обобщённые перемещения , соответствующие групповым неизвестным :

Приведённые массы , соответству-
ющие групповым неизвестным :

С

a

a

С

a

a

yi

yk

– симметрич.

– обратносим.

Jk

С

С

учёт симметрии в динамических расчётах
Собственные колебания
Упрощения динамических расчётов симметричных систем

при использовании групповых инерционных сил

Гармонические вынужденные колебания

Уравнение частот собственных колебаний:

Спектр частот
симметричных
колебаний

Спектр частот
обратносимметричных
колебаний

Полный спектр частот

Амплитуды динамических усилий:

При симметричных воздействиях
( нагрузках )

При обратносимметричных воздействиях ( нагрузках )

учёт симметрии в динамических расчётах
Собственные колебания
Упрощения динамических расчётов симметричных систем

при использовании групповых инерционных сил

Гармонические вынужденные колебания

Уравнение частот собственных колебаний:

Спектр частот
симметричных
колебаний

Спектр частот
обратносимметричных
колебаний

Полный спектр частот

Амплитуды динамических усилий:

При симметричных воздействиях
( нагрузках )

При обратносимметричных воздействиях ( нагрузках )

asim

sim

sim

учёт симметрии в динамических расчётах
Собственные колебания
Упрощения динамических расчётов симметричных систем

при использовании групповых инерционных сил

Уравнение частот собственных колебаний:

Спектр частот
симметричных
колебаний

Спектр частот
обратносимметричных
колебаний

Полный спектр частот

asim

sim

sim

J2

J1

J3

3m

m

m

учёт симметрии в динамических расчётах
Прием разделения симметричной системы по линии

симметрии

С

F

q

С

F/2

q/2

С

F/2

q/2

F/2

F/2

q/2

q/2

F/2

q/2

F/2

q/2

m/2
Im/2

m/2
Im/2

J2

J1

J3

J2(1)

J1

J3

J2(2)

J4

J5

nsim = 3

nasim = 5

n = 8

Симметричная
составляющая
амплитудной
нагрузки

Антисимметричная
составляющая
амплитудной
нагрузки

u = 0
θ = 0

u = 0

v = 0

v = 0

учёт симметрии в динамических расчётах
Связь между исходными неизвестными y

и обобщёнными координатами :

матрица линейного преобразования
неизвестных

Групповые перемещения масс. Обобщённые координаты

2. Инерционные силовые факторы, соответствующие обобщённым координатам

Из условия

Основные неизвестные
( обобщённые координаты ):

Исходные ( групповые )
неизвестные:

1. Приведённые (обобщённые) массы, соответствующие обобщённым координатам

учёт симметрии в динамических расчётах
Связь между
исходными неизвестными y
и

обобщёнными
координатами :

матрица ηy
линейного
преобразования
неизвестных

Группировка перемещений масс. Обобщённые координаты

2. Инерционные силовые
факторы, соответствующие
обобщённым координатам

Исходные
( групповые )
неизвестные

1. Приведённые (обобщённые) массы, соответствующие обобщённым координатам

П р и м е р 1

m

m

2m

3m

y1

y2

y3

y5

y2 = y3 = y4

y6

y4

EI = ∞

Массы, соответствующие исходным ( групповым )
неизвестным:

Основные
неизвестные
(обобщённые
координаты)

h/2

h/2

=diag [ 6,25 mh2 2m 3m ]

= [ h (J1/2+J2+J3+J4) J5 J6 ]т

J1

J2

J3

J4

J5

J6

Силы инерции
масс:

учёт симметрии в динамических расчётах
Связь между исходными
и новыми неизвестными:
матрица

ηy
преобразования
неизвестных

Группировка перемещений масс. Обобщённые координаты

2. Инерционные силовые факторы, соответствующие новым неизвестным

Исходные
неизвестные
(по центру массы):

1. Приведённые массы,
соответствующие новым неизвестным

П р и м е р 2

m

y1

y2

Характеристики
массы, соответст-вующие исходным
неизвестным:

lm

em

y3

J1

J2

J3

em

Неточечная масса

Om

O

Новые
неизвестные
(в точке О при-
крепления массы):

Недиагональная
матрица масс !

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 36» )
1. Как формируется расчётная схема системы с конечным числом степеней свободы масс
(КЧССМ) в случае вынужденного движения? ( 2 )
2. Какие динамические воздействия учитываются в расчёте и как они задаются? ( 2 )
3. Каким образом получаются и какой вид имеют дифференциальные уравнения
вынужденного движения системы с КЧССМ? ( 3 )
4. Какие рабочие гипотезы вводятся в расчёте на установившиеся вынужденные
гармонические колебания от вибрационных воздействий? ( 4 )
5. Что принимается за основные неизвестные в случае установившихся вынужденных
гармонических колебаний? ( 7 )
6. Основные ( канонические ) уравнения вынужденных колебаний системы с КЧССМ
при вибрационных воздействиях ( обычная и матричная формы записи ). ( 9 – 10 )
Чем они отличаются от уравнений для случая собственных колебаний? ( 9 – 10 )
7. Смысл основных уравнений в целом и их компонентов. Как определяются
коэффициенты и свободные члены уравнений? ( 9 – 10 )
8. Чем отличается матрица динамической податливости системы при гармонических
вынужденных колебаниях от аналогичной матрицы в случае собственных
колебаний? ( 10 )
9. Условие существования единственного решения системы уравнений установившихся
вынужденных колебаний. ( 10 )
10. Как вычисляются амплитуды динамических силовых факторов в заданной системе
от вибрационных воздействий? ( 11 )
11. В чём состоит сущность и назначение статической и кинематической проверок
результатов динамического расчёта сооружения на вибрационные воздействия?
Как выполняются эти проверки и какая из них является главной? ( 11 )
*) Только в режиме «Показ слайдов»

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 37» )
12. Что называется динамическим коэффициентом для некоторого параметра
напряжённо-деформированного состояния конструкции? ( 12 )
13. Какие значения могут принимать динамические коэффициенты при
в расчётах без учёта демпфирования колебаний? То же при ? ( 17 )
14. Почему динамические коэффициенты для разных параметров НДС отличаются
друг от друга и почему они неодинаковые в разных точках сооружения. ( 12 ) , ( 16 )
15. Каковы особенности резонанса в системах с конечным числом степеней свободы?
Какой из резонансов – на высоких или низких частотах собственных колебаний
сооружения – более опасен и почему? ( 17 )
16. Как записывается условие ненаступления резонанса при заданных воздействиях? ( 17 )
17. Какими конструктивными мерами можно изменять (регулировать) динамические
свойства сооружения и уменьшать неблагоприятные эффекты динамических
воздействий?
18. Как определяются расчётные усилия в сооружении при наличии статических
и динамических воздействий и как они используются в прочностных расчётах
элементов конструкций? ( 17 )
19. Общий алгоритм расчёта системы с конечным числом степеней свободы
при установившихся колебаниях от вибрационных воздействий. – см. [ 3 ] из списка
рекомендуемых учебно-методических изданий
20. Как при использовании метода перемещений в динамических расчётах систем
с конечным числом степеней свободы масс назначаются расчётные узлы
и формируется основная система? ( 18 )
21. На какие две группы разделяются основные неизвестные Z ( 19 ) и соответственно
уравнения метода перемещений? ( 20 )
*) Только в режиме «Показ слайдов»

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 38» )
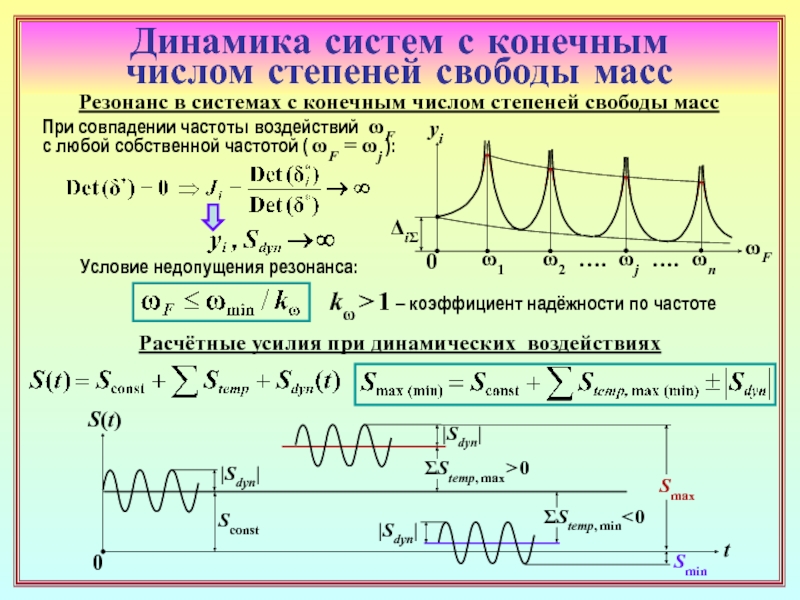
22. Чем отличаются уравнения 1-й и 2-й групп? ( 21 )
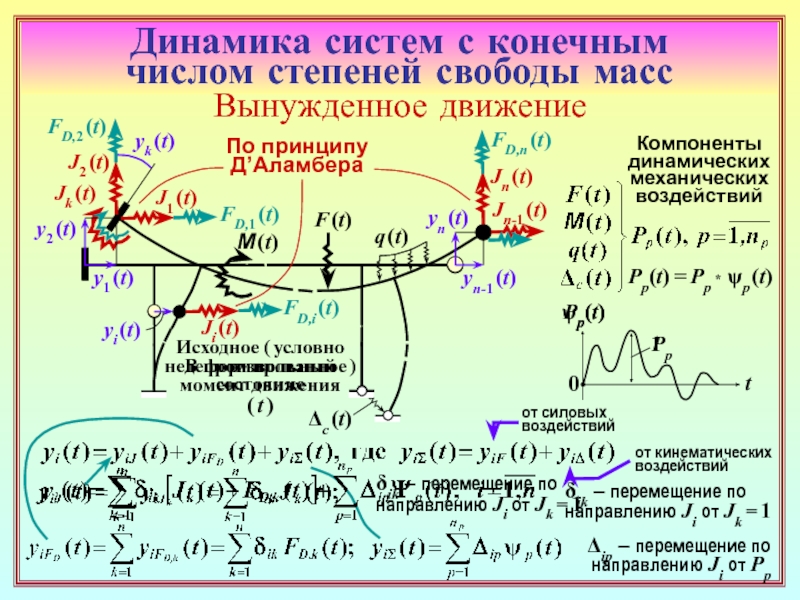
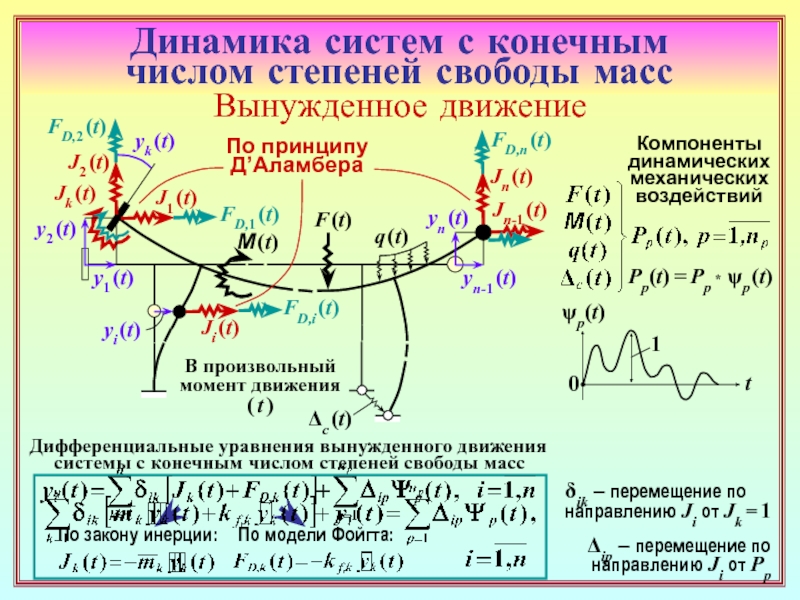
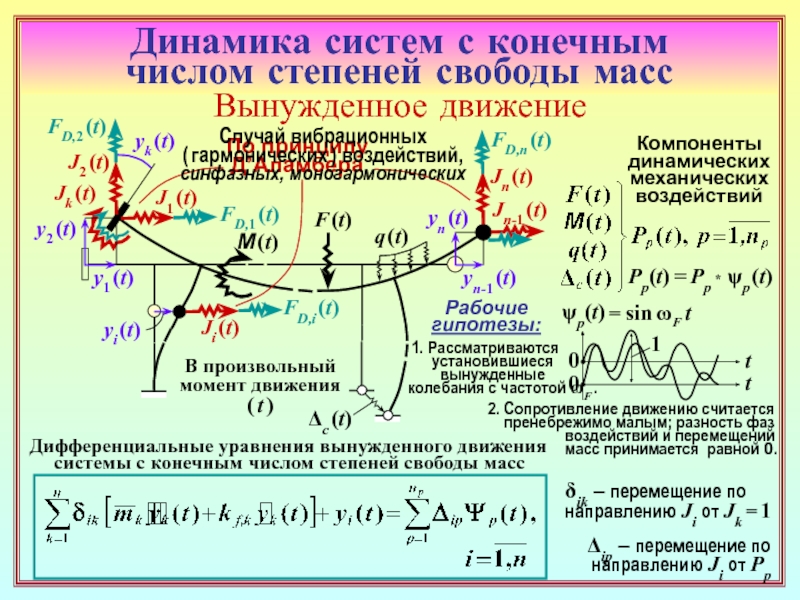
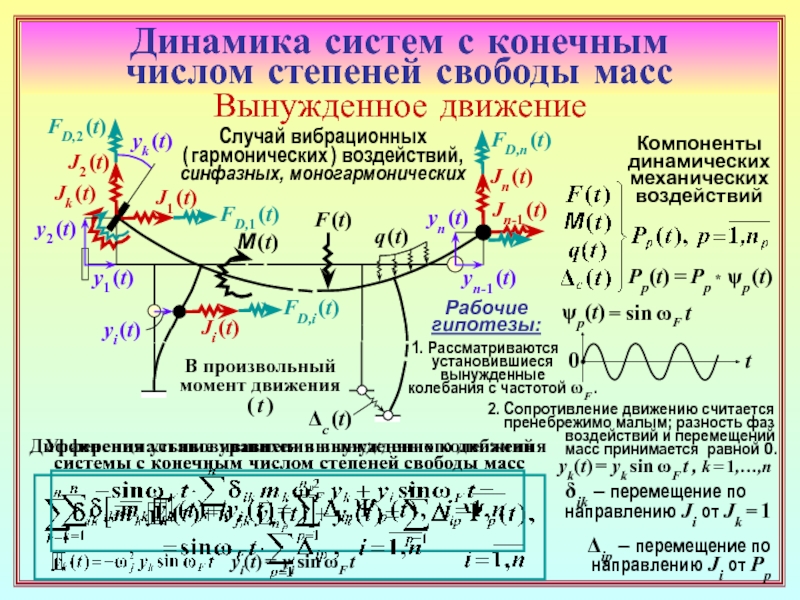
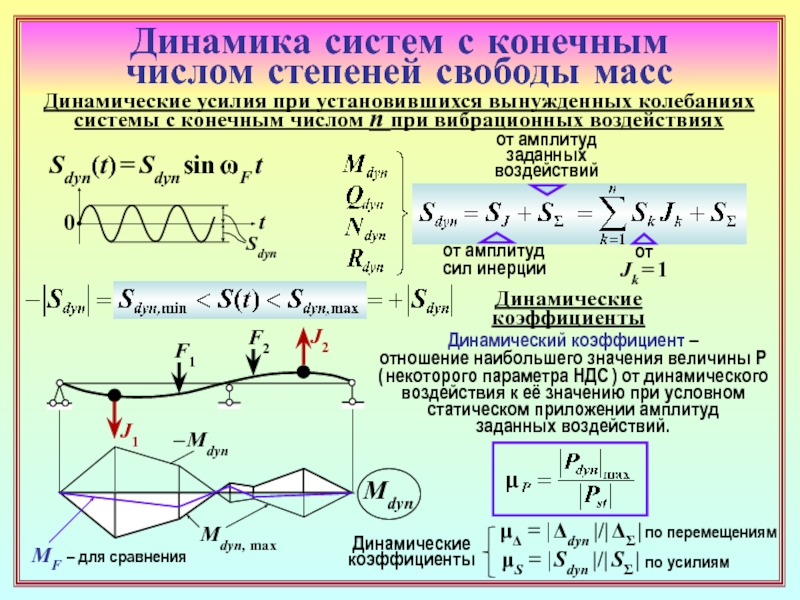
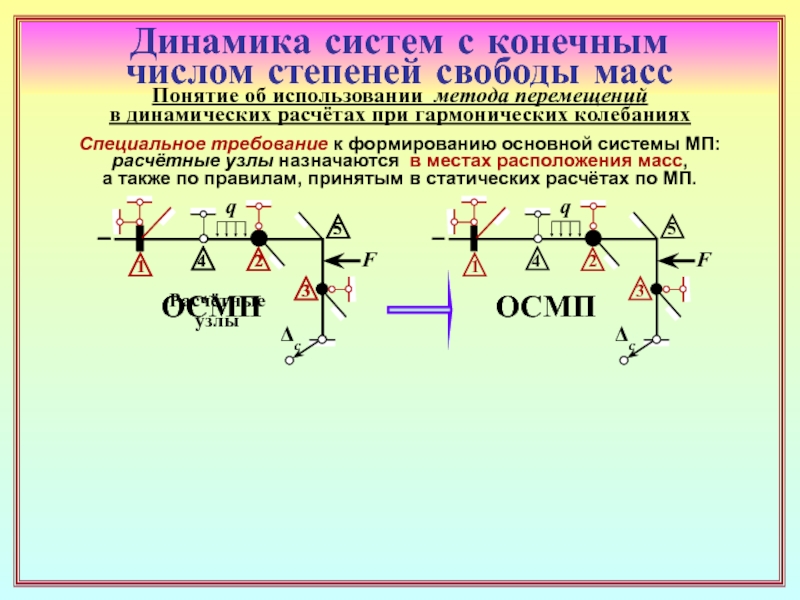
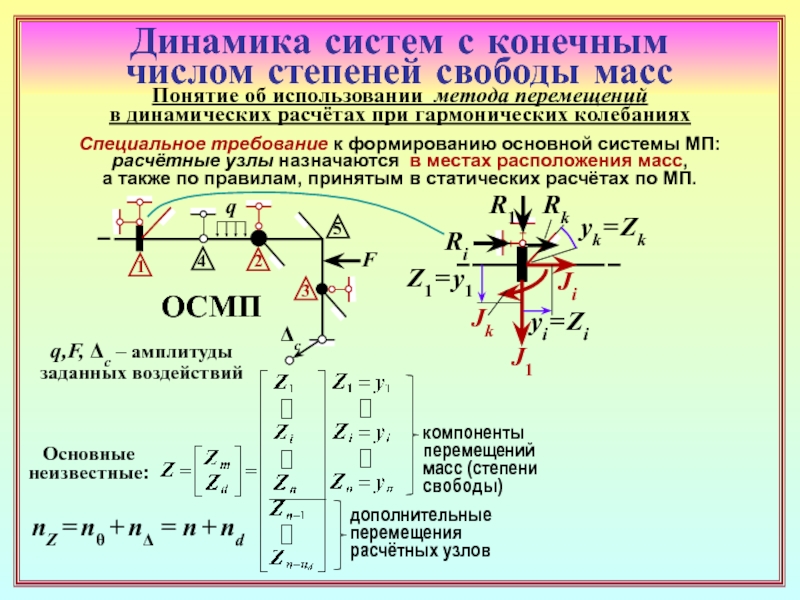
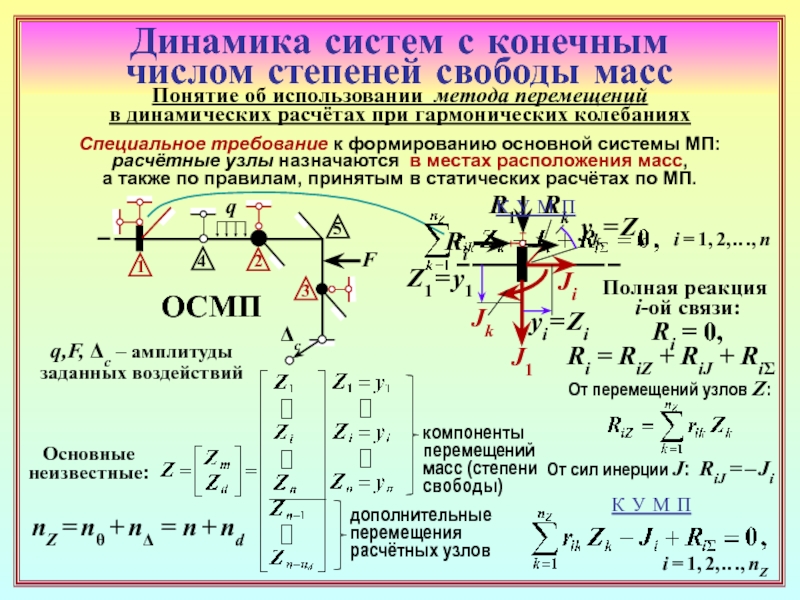
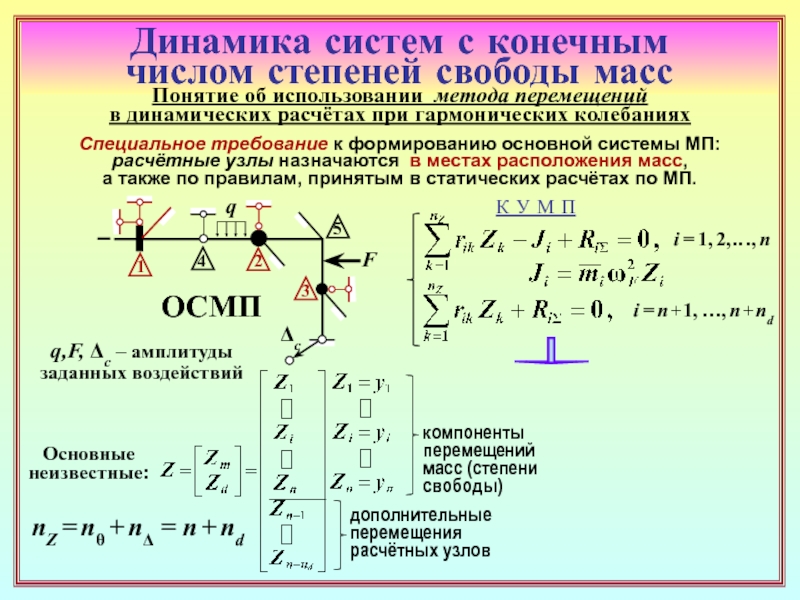
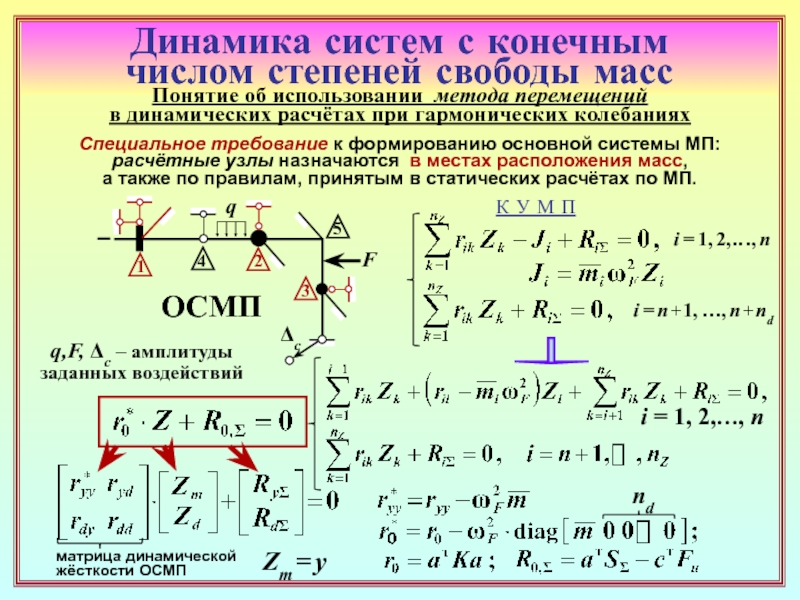
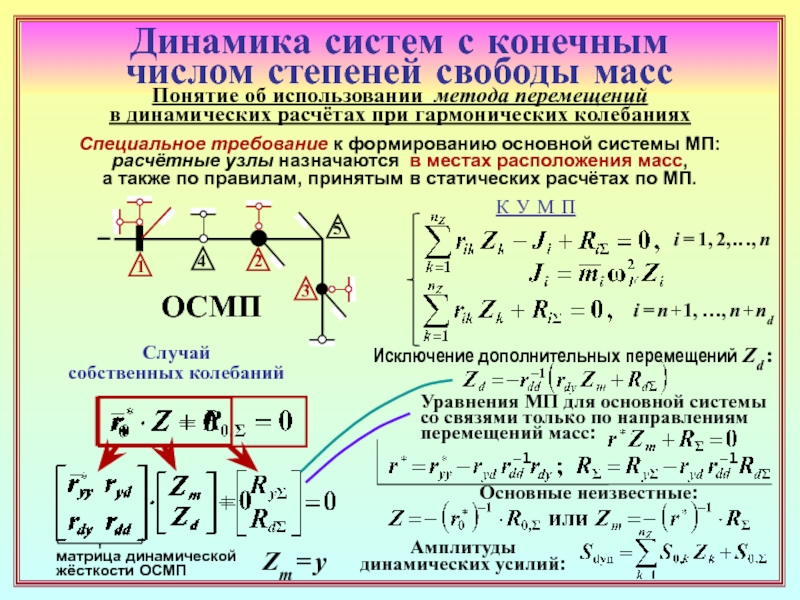
23. Как формируется матрица динамической жёсткости основной системы метода
перемещений (ОСМП) при гармонических колебаниях? В какой её части присутствуют
динамические характеристики? ( 22 )
24. Чем различаются матрицы динамической жёсткости ОСМП в расчётах на установив-
шиеся гармонические вынужденные колебания и на собственные колебания? ( 22 ) , ( 26 )
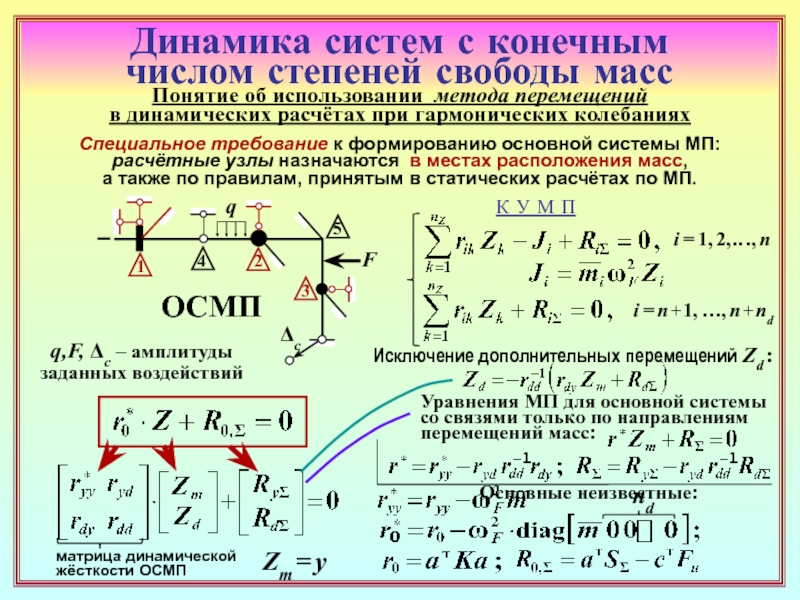
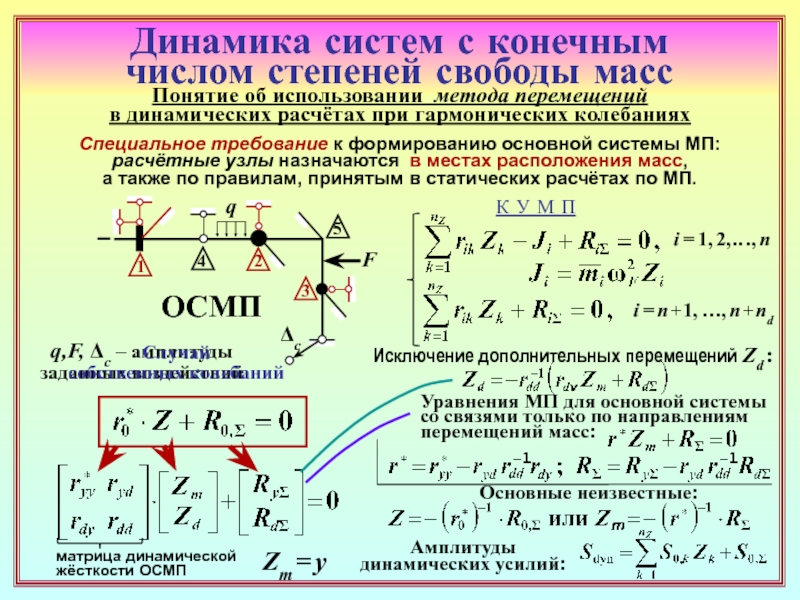
25. Каким образом можно получить систему уравнений метода перемещений только
с неизвестными перемещениями масс? ( 23 )
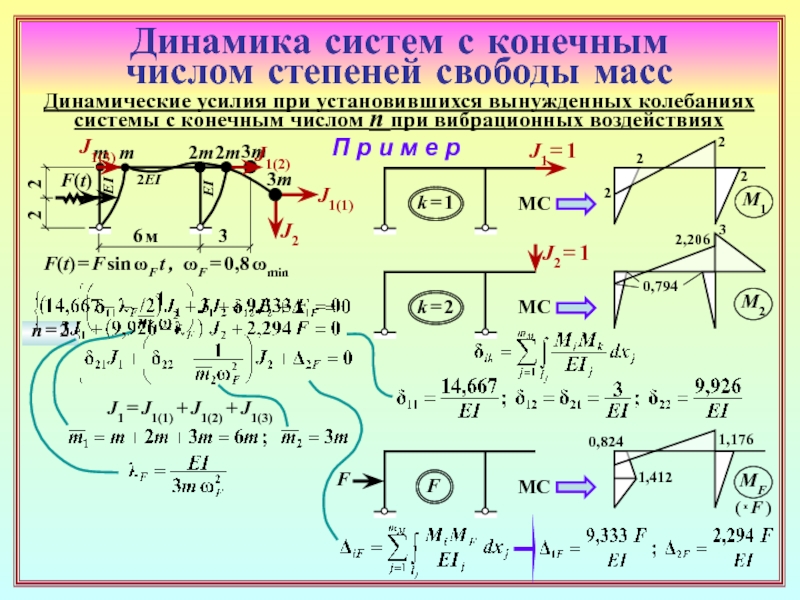
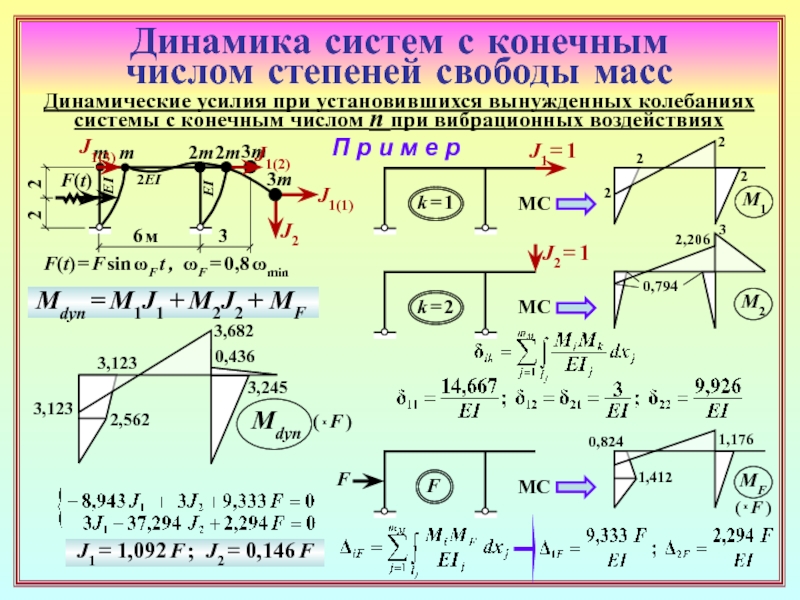
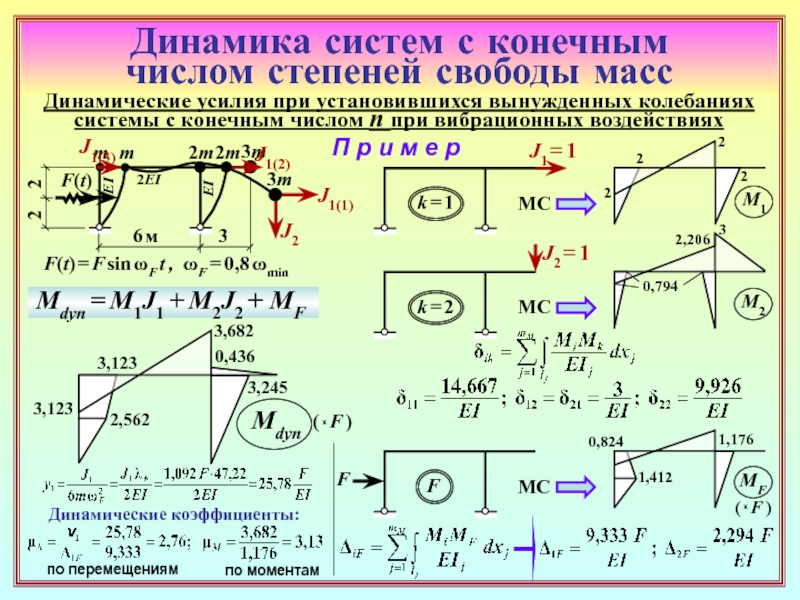
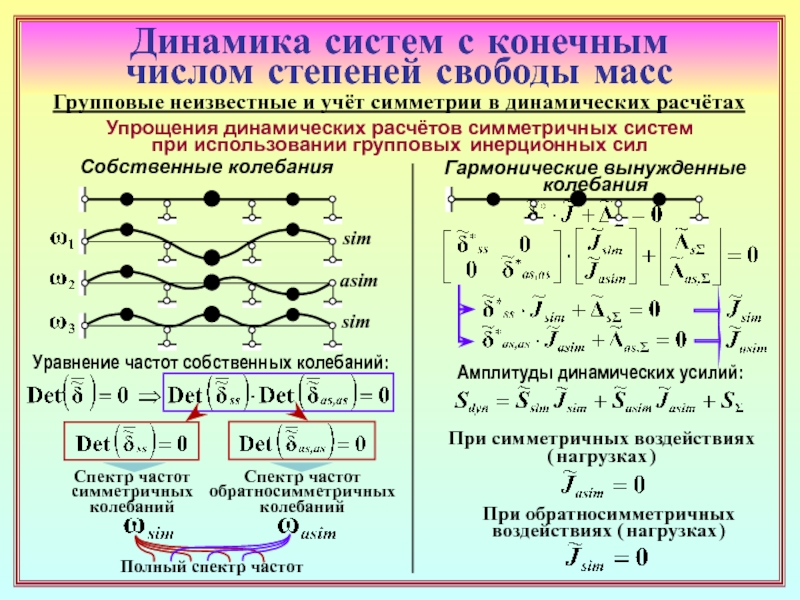
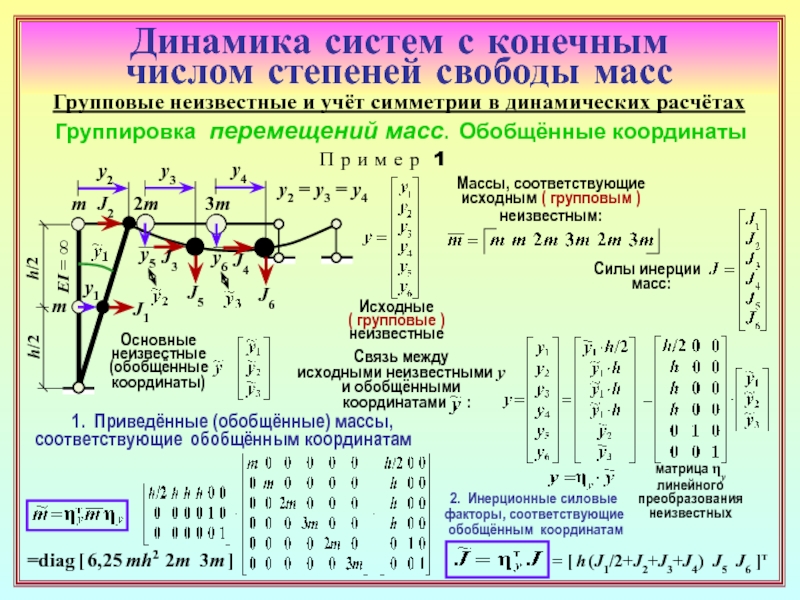
26. С какой целью в динамических расчётах сооружений применяется
группировка инерционных силовых факторов?
27. Привести примеры задач, в которых использование групповых
инерционных силовых факторов является необходимым из-за
особенностей рассчитываемого сооружения.
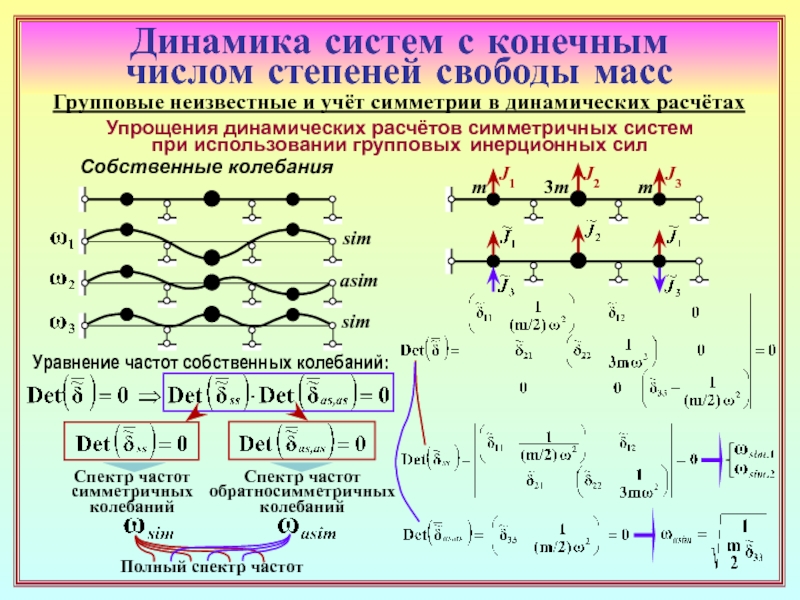
28. Какое условие используется для определения приведённой массы, соответствующей
некоторому групповому инерционному силовому фактору? ( 27 )
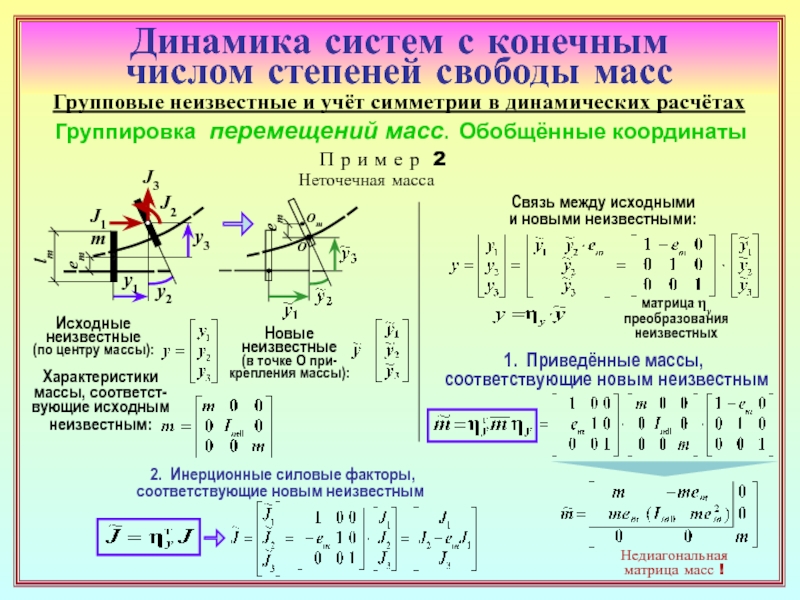
29. Как производится группировка сил инерции в симметричных системах? ( 30 )
30. Чему равна приведённая масса, соответствующая симметричной
( или обратносимметричной ) группе из двух сил инерции? ( 31 )
31. Какой выигрыш дает применение группировки сил инерции в задачах о собственных
колебаниях симметричных систем? ( 32, 33 ) В расчётах на вынужденные колебания
от произвольных вибрационных воздействий? ( 32 )
При симметричных или обратносимметричных динамических нагрузках? ( 32 )
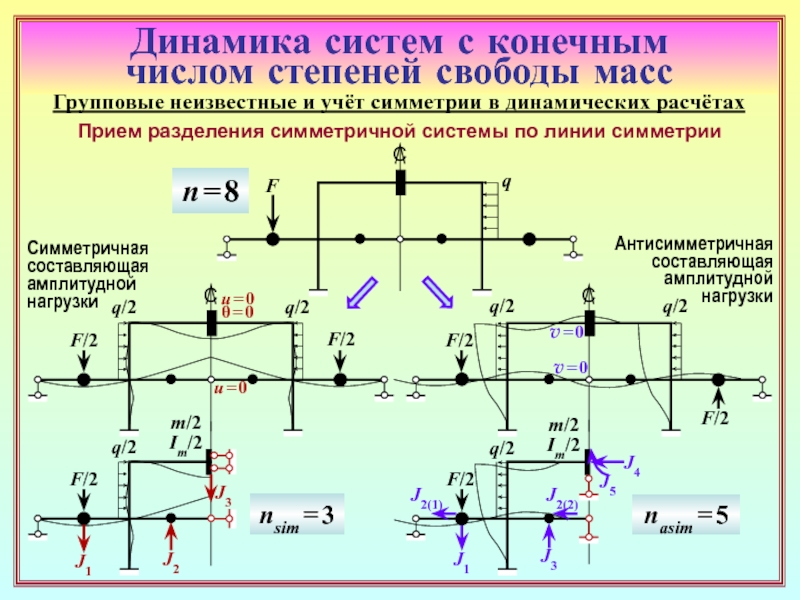
32. Какой прием расчёта симметричных сооружений является альтернативой
группировке инерционных силовых факторов? ( 35 )
*) Только в режиме «Показ слайдов»

см. [ 3 ]
из списка
рекомендуе-
мых учебно-методичес-
ких изданий