Теория вероятностей и математическая статистика

Математическая статистика
3. Планирование эксперимента.
Задачи оптимизации
4. Понятие о некорректных

задачах экспериментальной физики

4. Понятие о некорректных задачах
экспериментальной физики

и в быту
Принятие оптимальных решений
Азартные игры

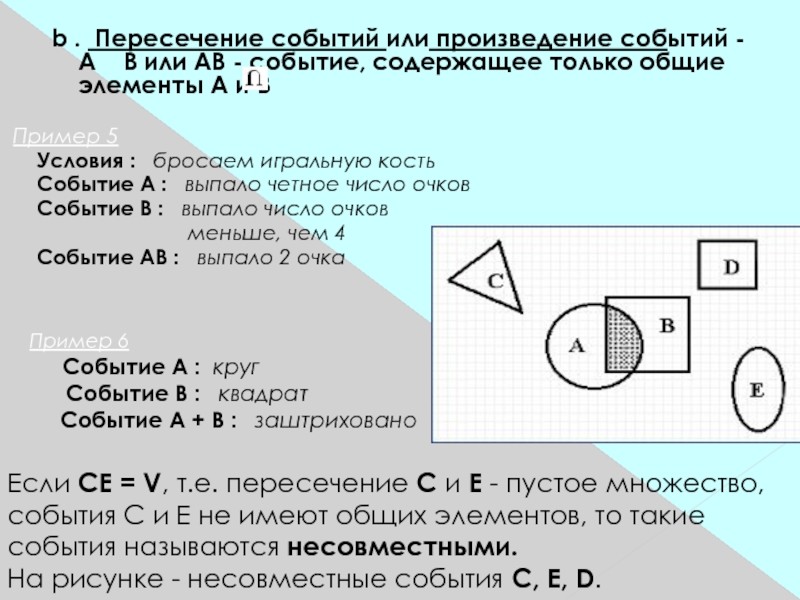
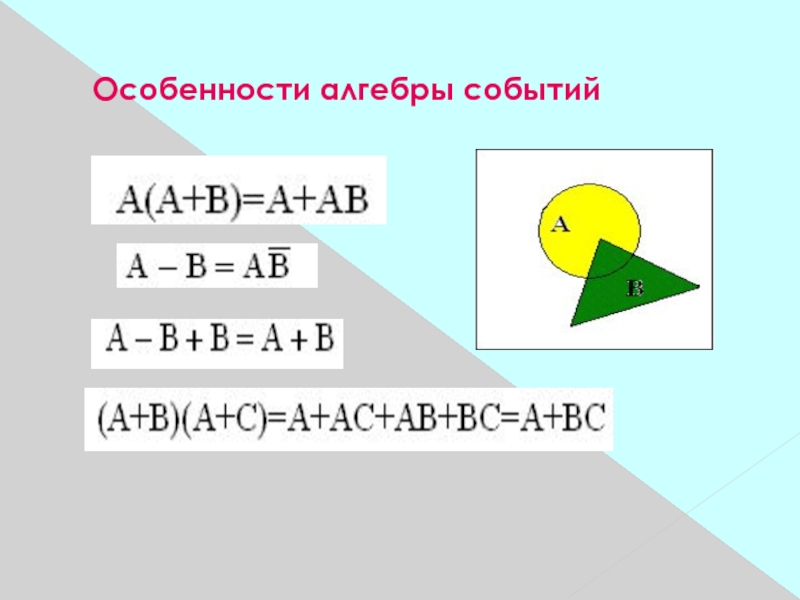
двенадцать молодых людей были застигнуты, когда они играли на деньги

в «семерку». Дело подлежало рассмотрению в суде. Защитник пытался доказать , что это не азартная игра, а наука. Над ним смеялись. Адвокат предложил :
– Назначьте двенадцать присяжных, шестерых, кто стоит за удачу, и шестерых, кто стоит за науку. Пусть возьмут две колоды карт, и идут в совещательную комнату.

На рассвете присяжные вышли в зал заседания, и их старшина,
прочитал вердикт: «Игра, известная под названием „семерка“
является безусловно не азартной, а научной игрой. В пользу
нашего решения свидетельствует то, что сторонники теории
удачи проигрались до последнего цента, и их деньги перешли
к представителям противной теории».

решения задач, связанных с выявлением возможного хода процессов, на которые

влияют случайные факторы(например: сколько бракованных изделий будет изготовлено).

статистическая физика
-Атомная и ядерная физика
-Квантовая механика
-Метрология, стандартизация и сертификация
-Основы теории

управления
-Теория принятия решений

5 по статистике)
Зачет
Использовать:
/dfe.karelia.ru
Учебная деятельность
Программы курсов
Задачи для самостоятельной работы
Методические

пособия

и П.Ферма, где они производили анализ азартных игр. Советские и

русские ученые внесли важный вклад в ее развитие : П.Л. Чебышев, А.А. Марков, А.М. Ляпунов. Но превратил ее в полноправный раздел математики в 30х годах 20 века Андрей Николаевич Колмогоров.

Колмогоров Андрей Николаевич

Блез Паскаль

Пьер де Ферма́

Чебышев 
Пафну́тий Льво́вич

Марков Андрей Андреевич

Ляпунов Александр Михайлович

не определяется.
Событие - это то, что при определенных условиях может

произойти или не произойти. В общем случае событие - это множество элементов. (Иногда - один, иногда - бесконечное множество)

Алгебра событий

в мишень
Событие А : стрела попала в "десятку”
Мн-во элементов А : бесконечное множество точек, заполняющих "десятку"

называется элементарным. В примере 1 - это выпадение определенной грани, скажем - 4.

Событие, которое в данных условиях всегда происходит называется достоверным (U) В примере 1 - это выпадение любой грани.

Событие, которое в данных условиях никогда не происходит называется невозможным (V) В примере 1 - это одновременное выпадение двух или более граней при однократном бросании одной кости.

событий или сумма событий A U B или А + В - событие, содержащее все элементы

А и В

Пример 3  
Условия :   бросаем игральную кость Событие А :   выпало четное число очков Событие B :   выпало число очков меньше, чем 4
Событие A + B :   выпало 1, 2, 3, 4 или 6 очков

Пример 4  
Событие А :  круг
Событие B :   квадрат
Событие A + B :   заштриховано

или АВ - событие, содержащее только общие элементы А и

В

Пример 5  
Условия :   бросаем игральную кость
Событие А :   выпало четное число очков
Событие B :   выпало число очков
меньше, чем 4
Событие AB :   выпало 2 очка

Пример 6  
Событие А :  круг
Событие B :   квадрат
Событие A + B :   заштриховано

Если СЕ = V, т.е. пересечение С и Е - пустое множество, события С и Е не имеют общих элементов, то такие события называются несовместными. На рисунке - несовместные события С, Е, D.

А c В), если, когда происходит A, то B обязательно происходит ,

т.е. все элементы А входят и в В, но В может содержать и элементы, не входящие в А.

Пример 7     
Условия :   бросаем игральную кость  
Событие А :   выпало два очка       
Событие B :   выпало четное число очков     Элементы А входят в В, или  A c B  

Если А c В и одновременно В c А, т.е. все элементы у А и В - общие, то такие события называются равносильными, или равными.

событий.
e .  Событие, дополняющее данное (А) до достоверного, называется противоположным данному и

обозначается чертой сверху .
Т.е.  

f .  Все несовместные » события, в сумме составляющие достоверное образуют полную группу событий.

пространстве элементарных событий, строят поле событий.
Поле

событий - это множество событий, которое включает в качестве элементов :
1 .  достоверное событие,
2 .  невозможное событие,
3 .  все элементарные события данного пространства,
4 .  все события, которые на этом пространстве можно построить путем сложения (объединения) событий, путем перемножения (пересечения) событий, а также путем взятия противоположных событий от любого уже построенного.

называемое вероятностью этого события и удовлетворяющее следующим аксиомам:

Определение понятия вероятности
по  Колмогорову :

1. Р(А) ≥ 0 ;
2. Р(U) = 1, U - достоверное событие ;
3. Р(А+В) = Р(А) + Р(В) , если А и В - несовместны.

 


A=A-AB+AB
A=A-AB+AB 1. P(A)=P(A-AB)+P(AB)
A+B=A-AB+B

2. P(A+B)=P(A-AB)+P(B)

несовместныы

несовместныы

Вычтем из второго равенства первое

4. Если А c В , то Р(В) ≥ Р(А) 

B=A+BA P(B)=P(A)+P(BA)

несовместныы

>=0

конечно и равно n, а событие А включает в себя

m элементарных событий, то Р(А) = m/n ;

Классическое определение вероятности

Для решения задач часто надо использовать
формулы комбинаторики.

Перестановки

Размещения

Сочетания

сумма очков равна 10 ?  В этих условиях n = 36, а событие

А: сумма очков равна 10 происходит в m = 3 случаях, следовательно Р(А) = 3/36 = 1/12 .

Пример 2. 10 человек рассаживаются за круглым столом по жребию (случайным образом). Какова вероятность того, что Вы окажетесь рядом с конкретным наиболее приятным Вам человеком ?   Решение:   Для Вашего друга осталось 9 мест, из них условию- быть рядом с Вами-  удовлетворяют 2, , следовательно Р=2/9.

часто используется при решении задач и его называют "классическим определением

вероятности". Однако, это ни в коем случае не является определением понятия вероятность, т.к. в качестве определения оно логически противоречиво и область его применения ограничена частным случаем конечного числа равновероятных элементарных событий. (т.е. само определение ссылается на определяемое понятие)

человек. Какова вероятность того, что хоть у кого-то совпадают дни

рождения?

человек. Какова вероятность того, что хоть у кого-то совпадают дни

рождения?
Найдем вероятность противоположного события : никто не родился в один день с товарищем.

При x<<1 exp(-x)~1-x

P(A)~0.7