TheSlide.ru

Задача №5

Содержание

1. Задача №5
2. Фирма реализует произведенную продукцию по цене p,
3. Решение.Учитывая, что прибыль представляет собой разность между
4. 1) Выполняем полное исследование функции П(q)
5. 1.1. Область определения D(П)=(0;+∞).
6. 1.2. Находим первую и вторую производную П’(q) и П’’(q)П’(q)=(10q-0,001q^3)’=10-0,003q^2П’’(q)=(10-0,003q^2)’=-0,006q
7. 1.3. Находим критические точки, решая уравнение П’(q)=010-0,003q^2=0q=57,7
8. 1.4. Наносим критическую точку на числовую ось,
9. 1.5. Найдем точку перегиба графика функции, решая
10. 1.6. Найдем, на каких интервалах график функции
11. 1.7. Сводим все полученные результаты в итоговую таблицу:Таблица 1.
12. 1.8. Строим схематический график функции.Рис.2. График зависимости прибыли от объема выпуска продукции.
13. 2) Очевидно, что оптимальным для фирмы является
14. Скачать презентанцию

Фирма реализует произведенную продукцию по цене p, а зависимость издержек C имеет вид

Слайды и текст этой презентации

Слайд 1Задача №5.
Работу подготовила:
Студентка 1 курса
1 Федорова А

Задача №5.Работу подготовила:Студентка 1 курса 1 Федорова А

Слайд 2Фирма реализует произведенную продукцию по цене p, а зависимость издержек

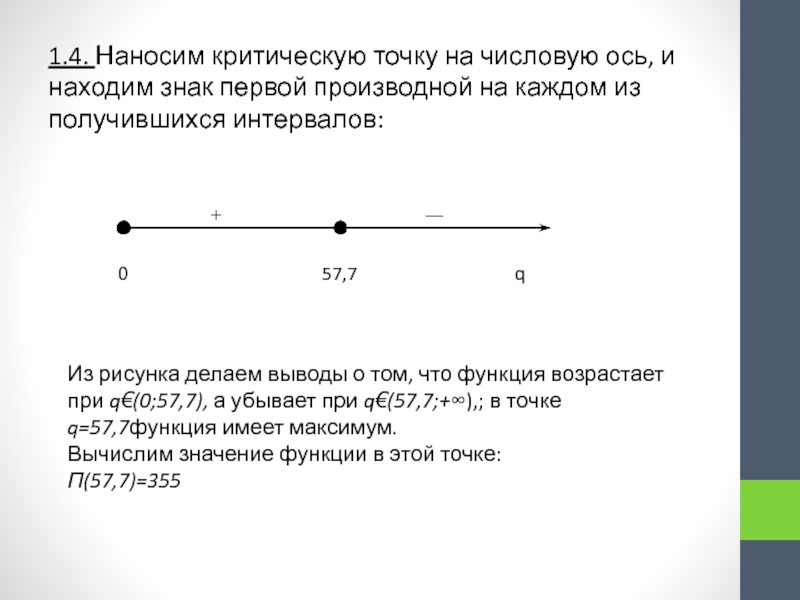
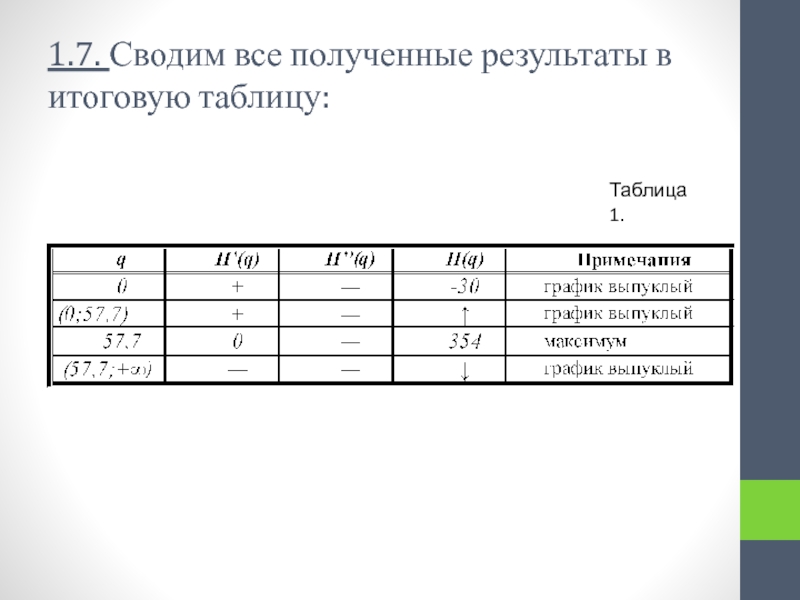
C имеет вид

, где q- объём производства.
Используя методы дифференциального исчисления:
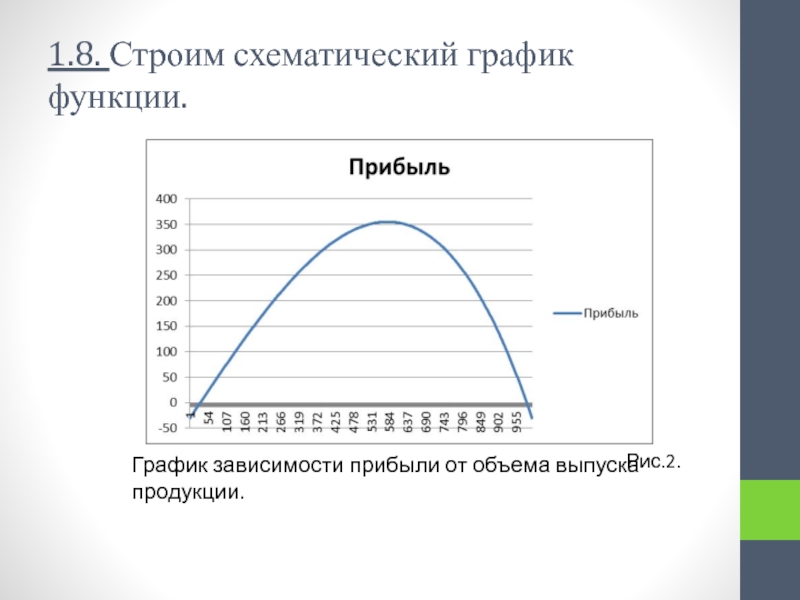
1) выполнить полное исследование функции зависимости прибыли фирмы П от объема производства q построить ее график.
2) Найти оптимальный для фирмы объем выпуска продукции и соответствующую ему прибыль.
a=50; b=0,001; c=30; p=60

Фирма реализует произведенную продукцию по цене p, а зависимость издержек C имеет вид

Слайд 3Решение.
Учитывая, что прибыль представляет собой разность между доходом и издержками,

и подставляя численные данные, получаем явный вид зависимости прибыли от

объема производства:

Решение.Учитывая, что прибыль представляет собой разность между доходом и издержками, и подставляя численные данные, получаем явный вид

Слайд 41) Выполняем полное исследование функции П(q)

1) Выполняем полное исследование функции П(q)

Слайд 51.1. Область определения D(П)=(0;+∞).

1.1. Область определения D(П)=(0;+∞).

Слайд 61.2. Находим первую и вторую производную П’(q) и П’’(q)
П’(q)=(10q-0,001q^3)’=10-0,003q^2
П’’(q)=(10-0,003q^2)’=-0,006q

1.2. Находим первую и вторую производную П’(q) и П’’(q)П’(q)=(10q-0,001q^3)’=10-0,003q^2П’’(q)=(10-0,003q^2)’=-0,006q

Слайд 71.3. Находим критические точки, решая уравнение П’(q)=0
10-0,003q^2=0
q=57,7

1.3. Находим критические точки, решая уравнение П’(q)=010-0,003q^2=0q=57,7

Слайд 81.4. Наносим критическую точку на числовую ось, и находим знак

первой производной на каждом из получившихся интервалов:
q
57,7
0
Из рисунка делаем выводы

о том, что функция возрастает при q€(0;57,7), а убывает при q€(57,7;+∞),; в точке q=57,7функция имеет максимум.
Вычислим значение функции в этой точке:
П(57,7)=355

1.4. Наносим критическую точку на числовую ось, и находим знак первой производной на каждом из получившихся интервалов:q57,70Из

Слайд 91.5. Найдем точку перегиба графика функции, решая уравнение П’’(q)=0

Так

как случай q=0 не представляет практического интереса, будем считать, что

график функции точек перегиба не имеет.

1.5. Найдем точку перегиба графика функции, решая уравнение П’’(q)=0 Так как случай q=0 не представляет практического интереса,

Слайд 101.6. Найдем, на каких интервалах график функции выпуклый, а на

каких—вогнутый.

Так как

на всей области определения, делаем вывод о том, что график функции выпуклый на всей области определения.

1.6. Найдем, на каких интервалах график функции выпуклый, а на каких—вогнутый.Так как

Слайд 111.7. Сводим все полученные результаты в итоговую таблицу:
Таблица 1.

1.7. Сводим все полученные результаты в итоговую таблицу:Таблица 1.

Слайд 121.8. Строим схематический график функции.
Рис.2.
График зависимости прибыли от объема

выпуска продукции.

1.8. Строим схематический график функции.Рис.2. График зависимости прибыли от объема выпуска продукции.

Слайд 132) Очевидно, что оптимальным для фирмы является объем выпуска, равный

57,7, при этом прибыль будет максимальна и составит 354.

Ответ в

данной задаче нет необходимости выписывать отдельно, так как он фактически содержится в таблице 1.

2) Очевидно, что оптимальным для фирмы является объем выпуска, равный 57,7, при этом прибыль будет максимальна и

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей