Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
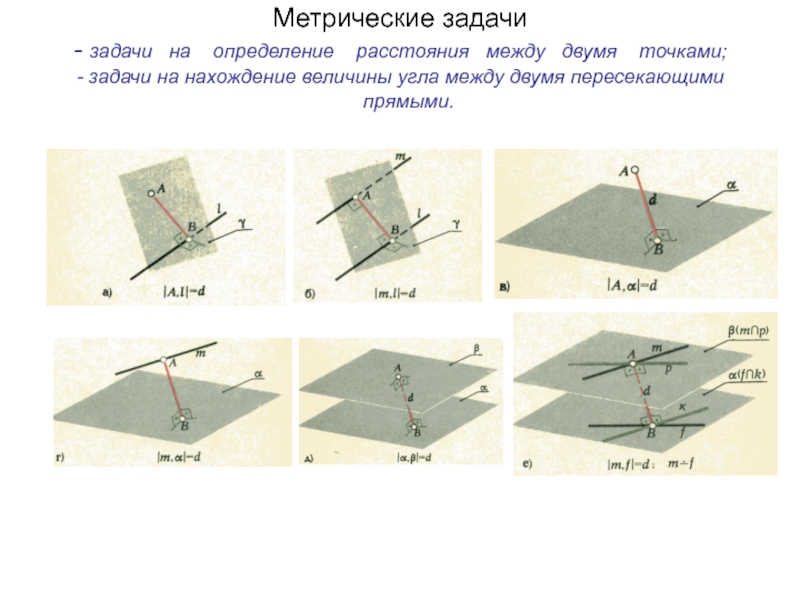
Метрические задачи
Содержание
- 1. Метрические задачи
- 2. Определение расстояния между точкой и плоскостью:расстояние от
- 3. Определение расстояния между плоскостями:расстояние между плоскостями определяется
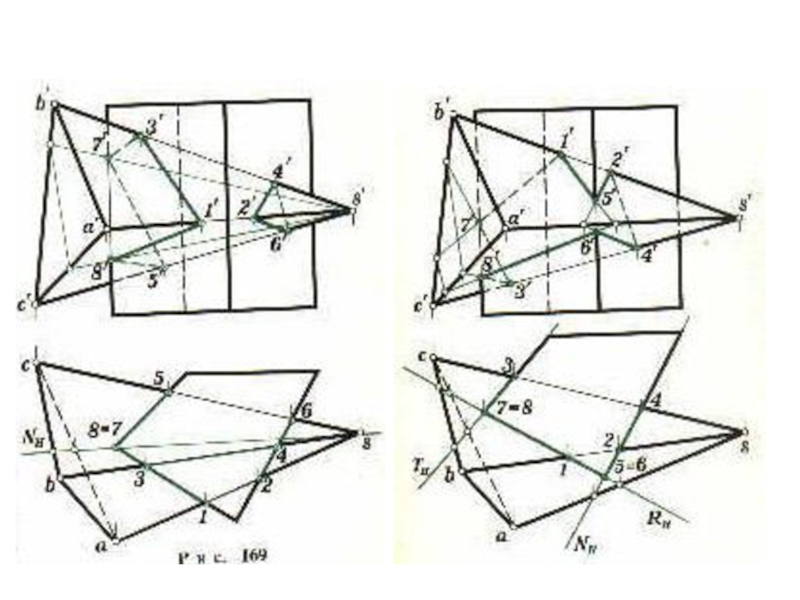
- 4. Определение расстояния между скрещивающимися прямыми:расстояние между скрещивающимися
- 5. Проекции плоских угловЕсли стороны угла не параллельны
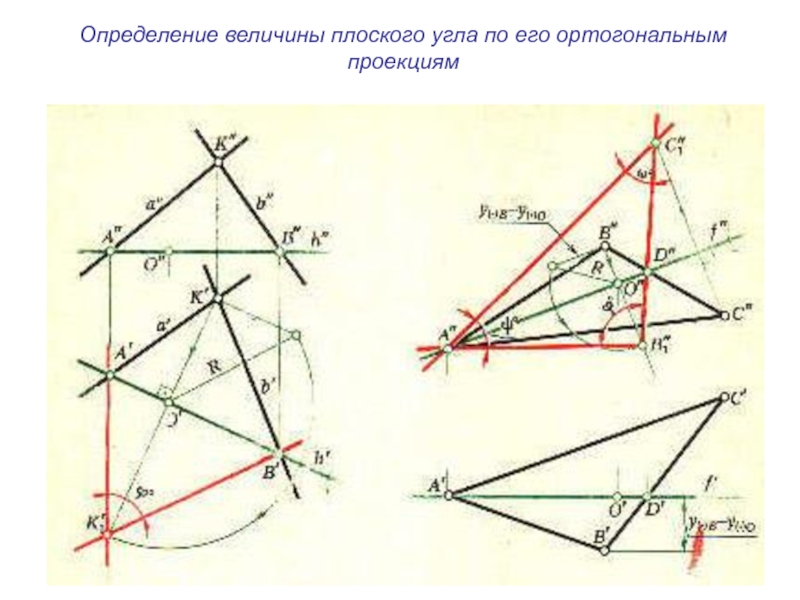
- 6. Определение величины плоского угла по его ортогональным проекциям
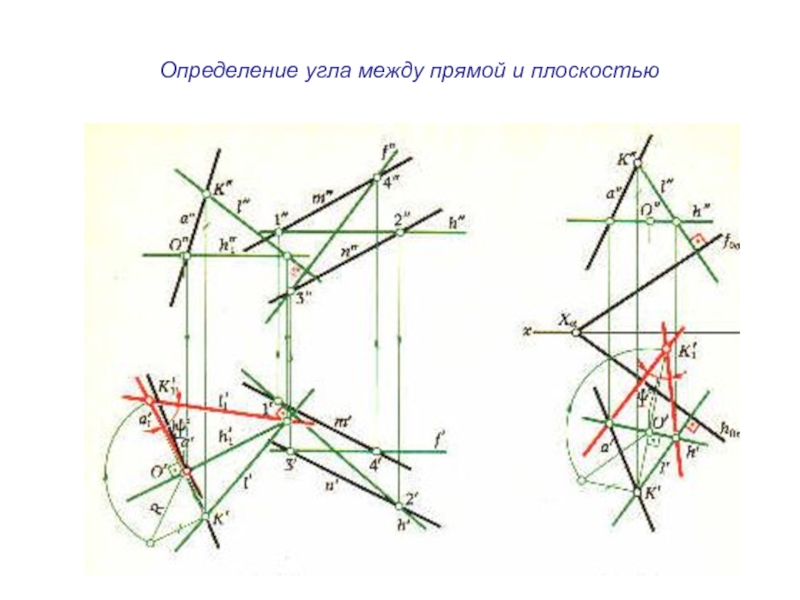
- 7. Определение угла между прямой и плоскостью
- 8. Определение угла между плоскостямимерой угла между двумя
- 9. Слайд 9
- 10. Слайд 10
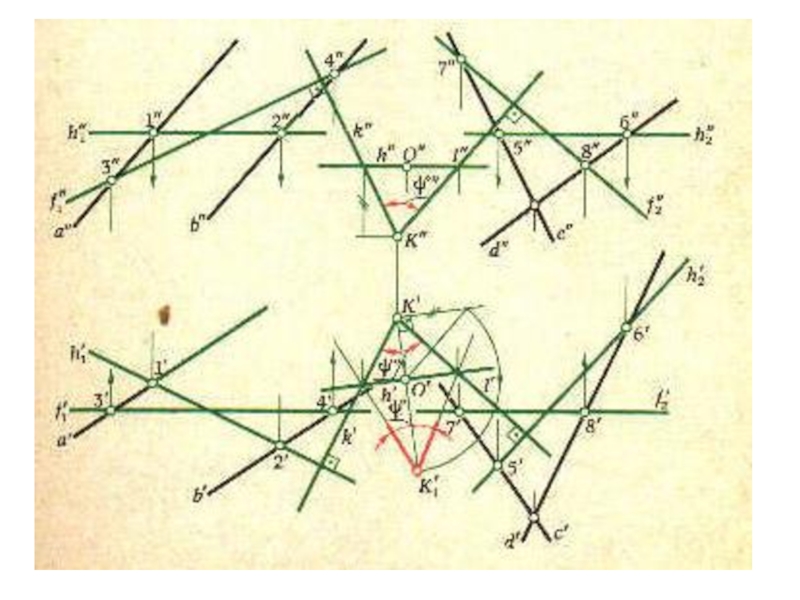
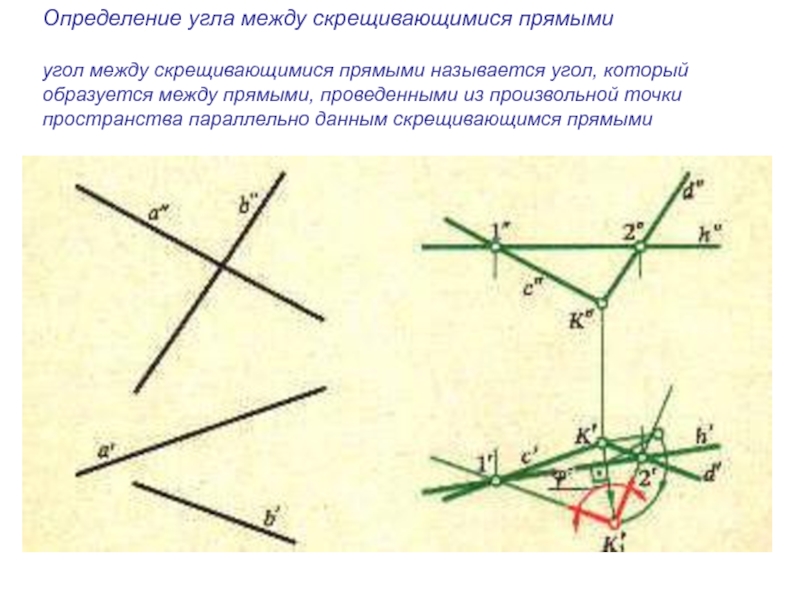
- 11. Определение угла между скрещивающимися прямымиугол между скрещивающимися
- 12. Позиционные задачизадачи на принадлежность:принадлежность точки линии,принадлежность точки
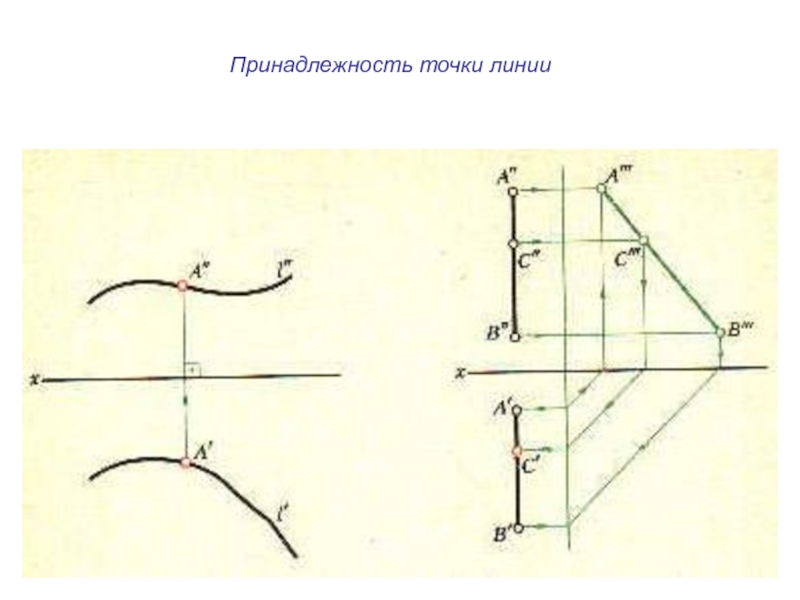
- 13. Принадлежность точки линии
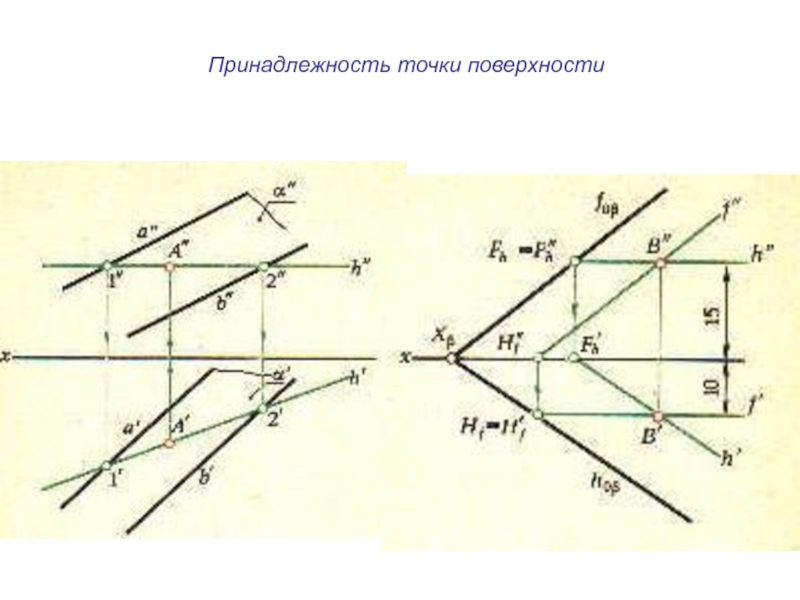
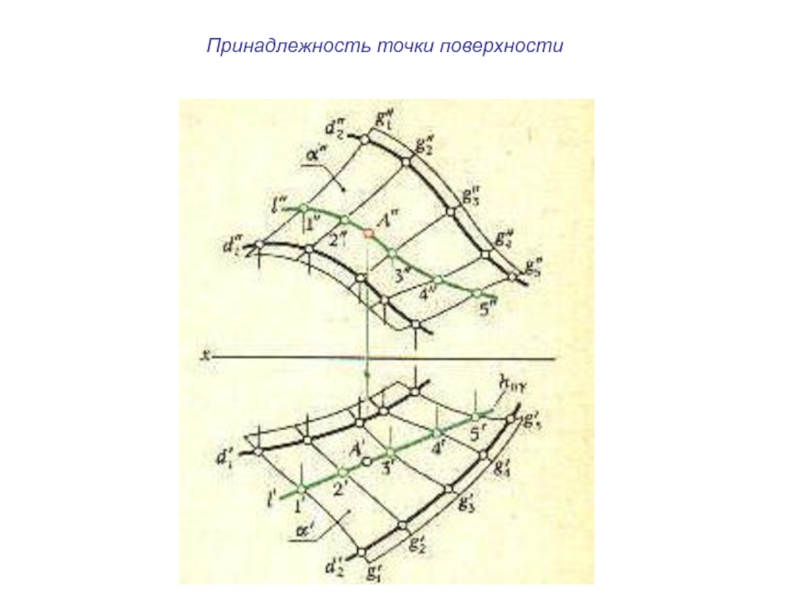
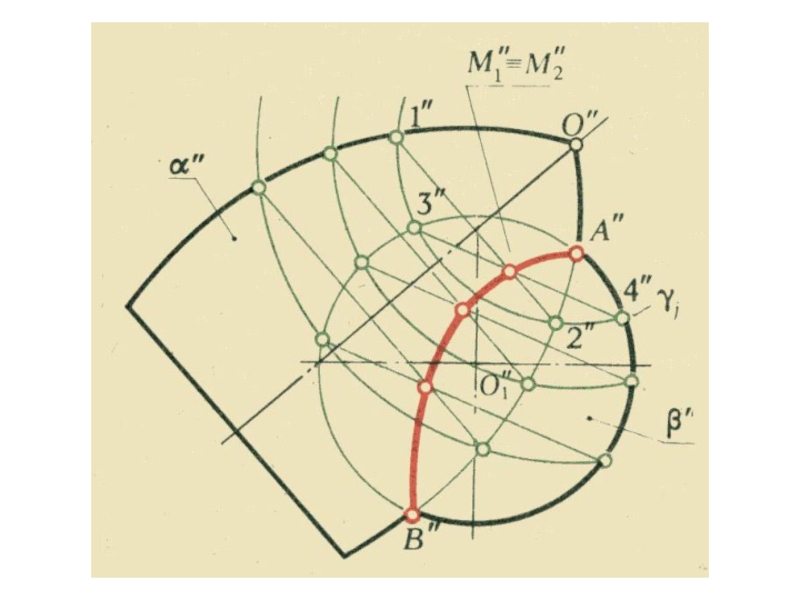
- 14. Принадлежность точки поверхности
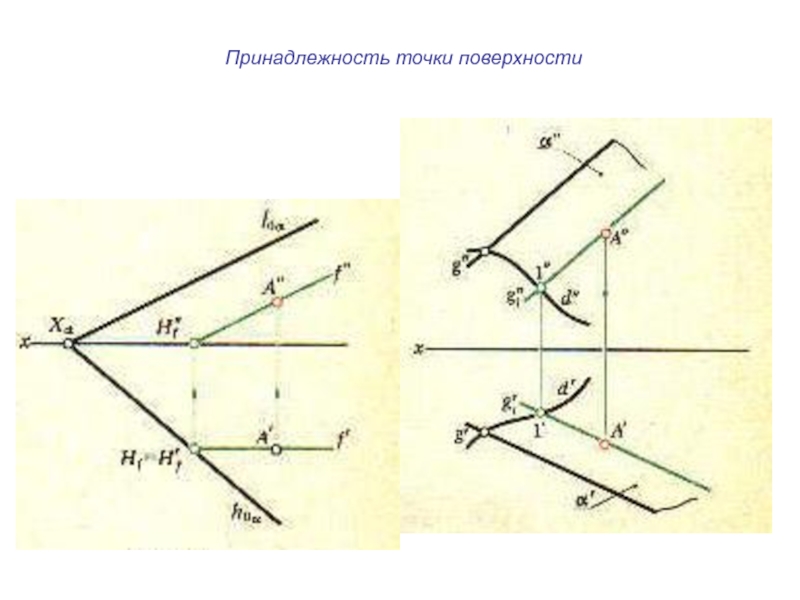
- 15. Принадлежность точки поверхности
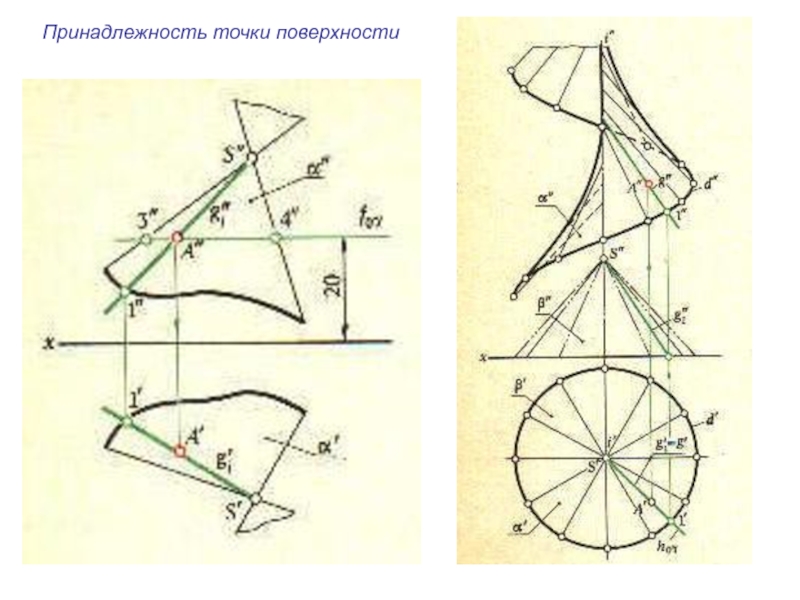
- 16. Принадлежность точки поверхности
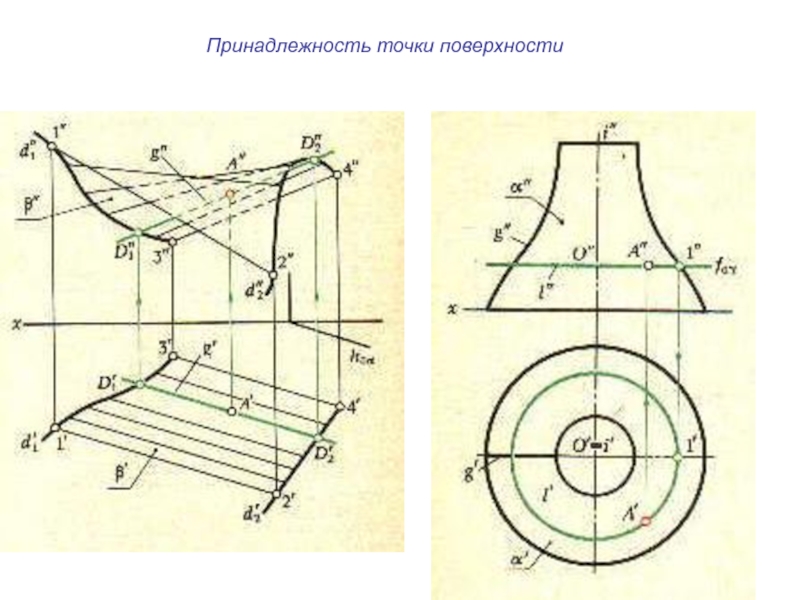
- 17. Принадлежность точки поверхности
- 18. Принадлежность точки поверхности
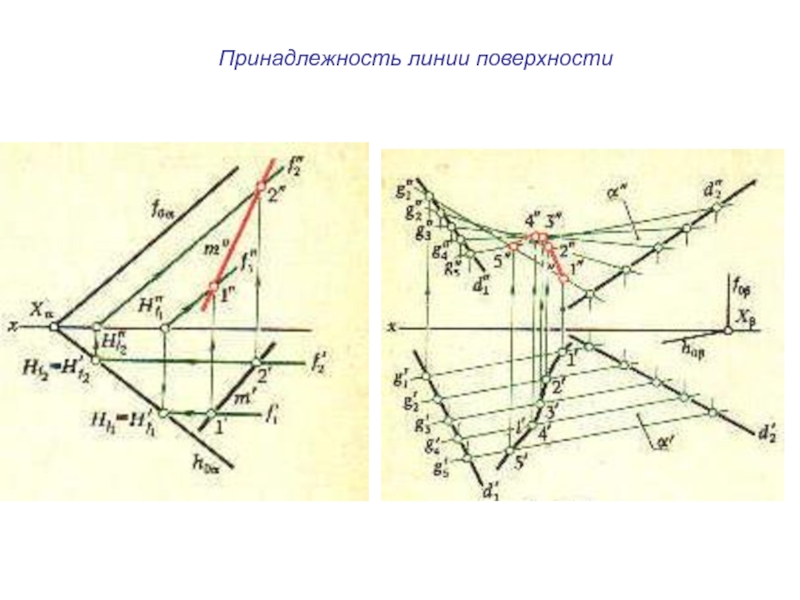
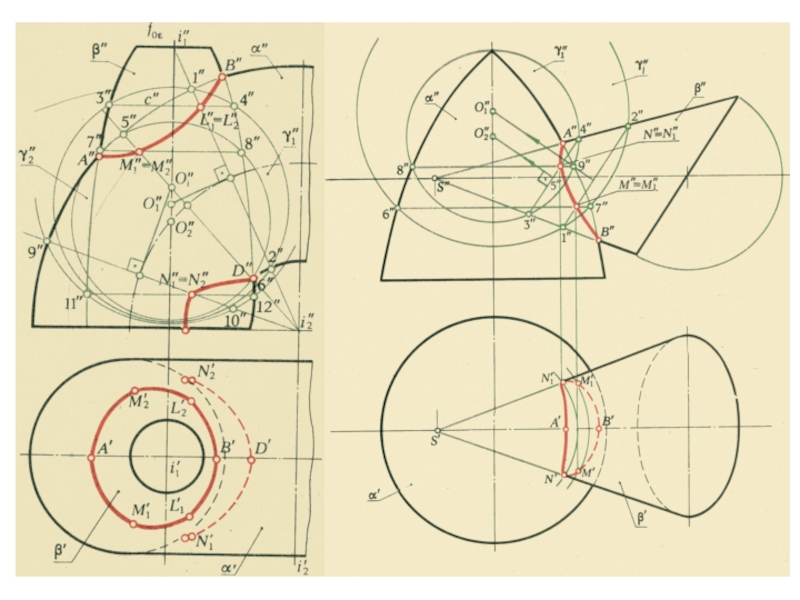
- 19. Принадлежность линии поверхности
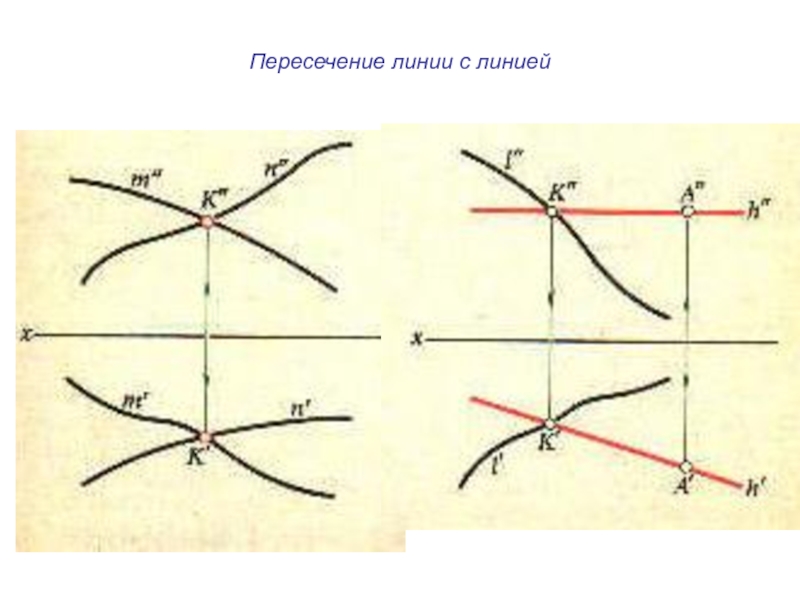
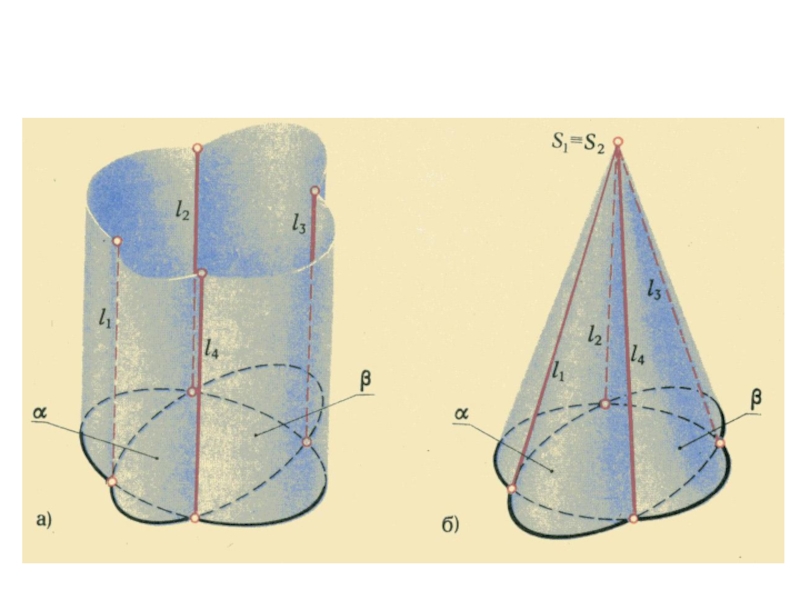
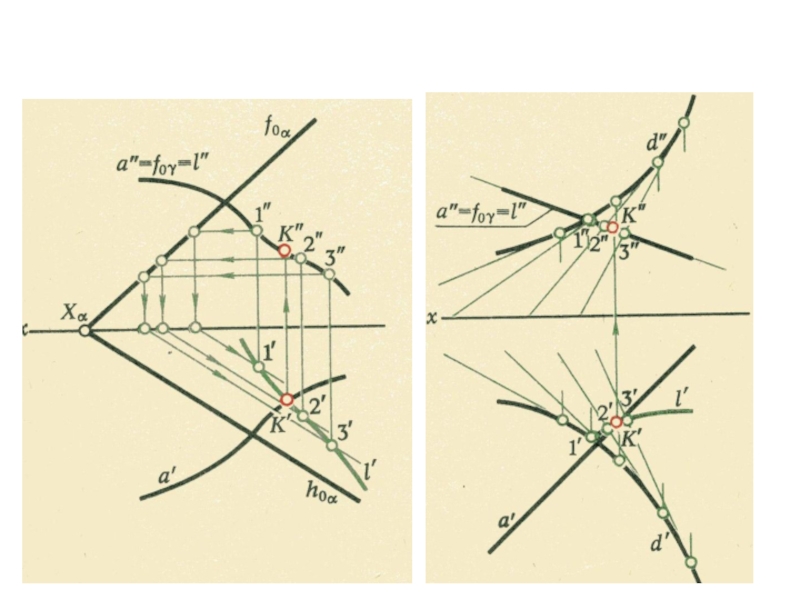
- 20. Пересечение линии с линией
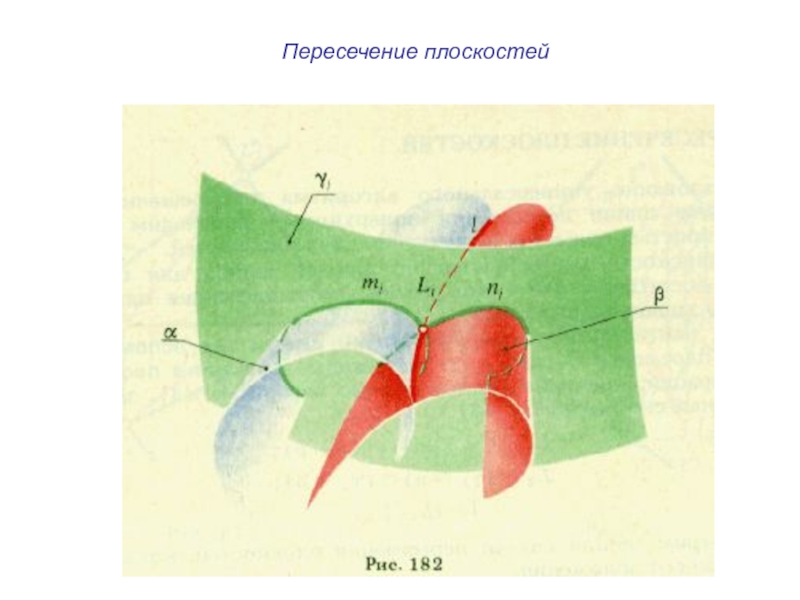
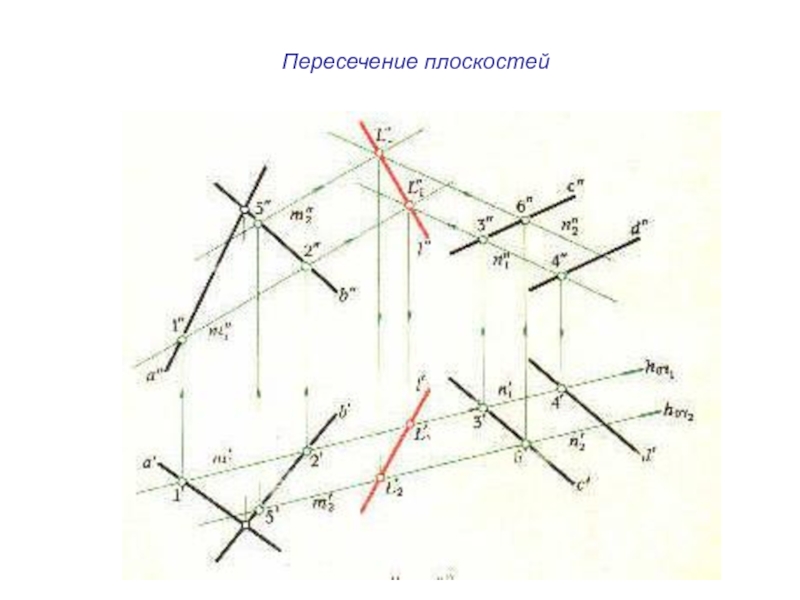
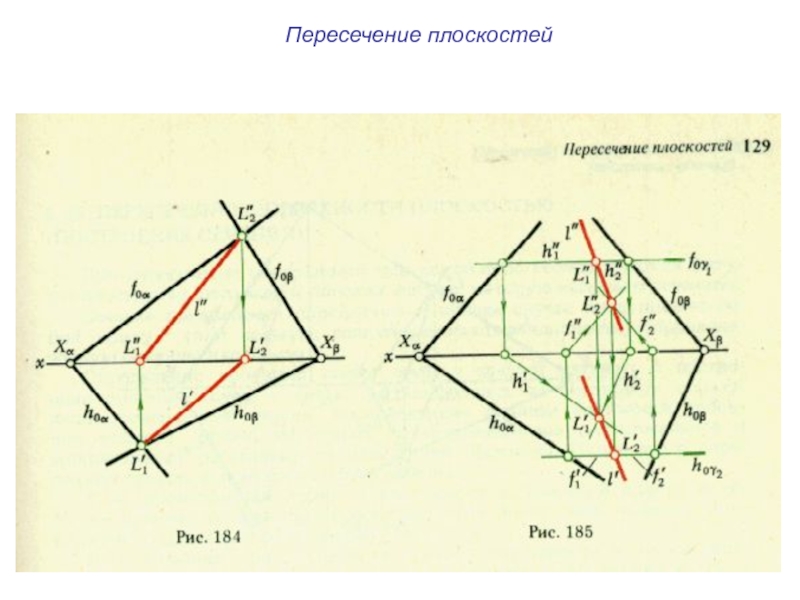
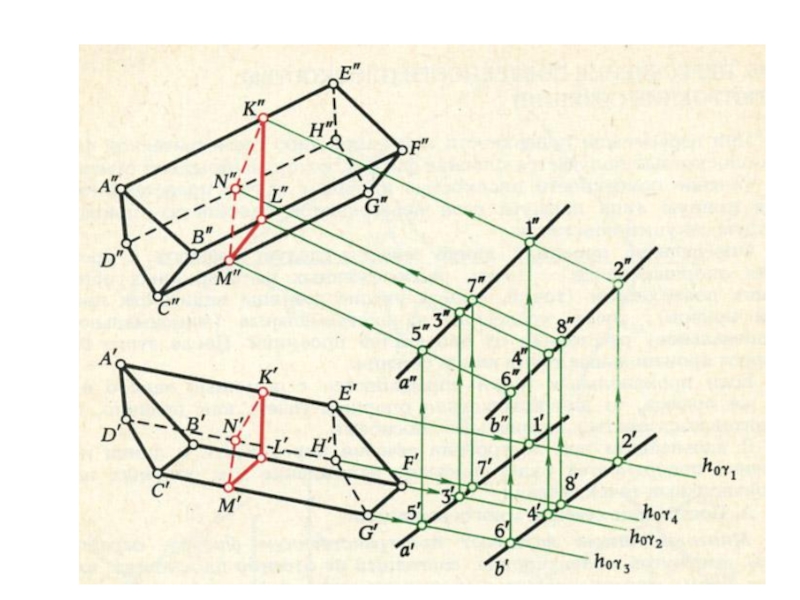
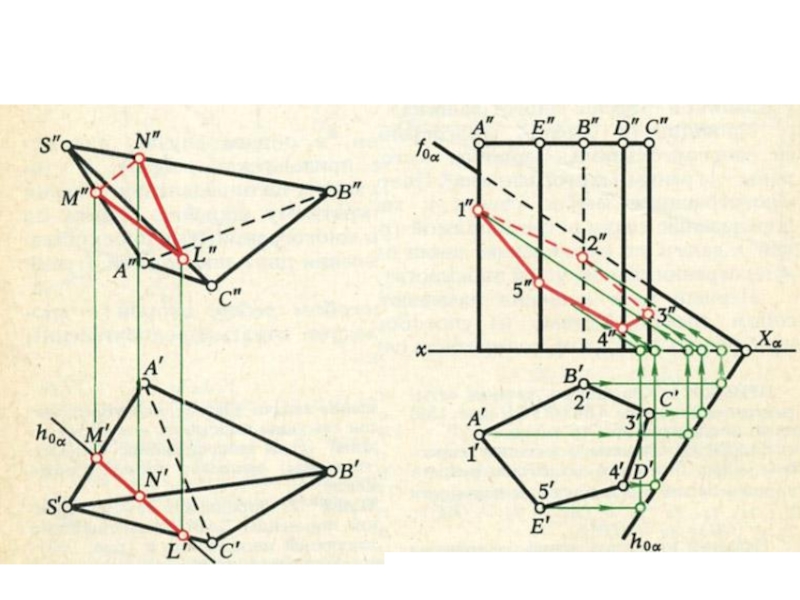
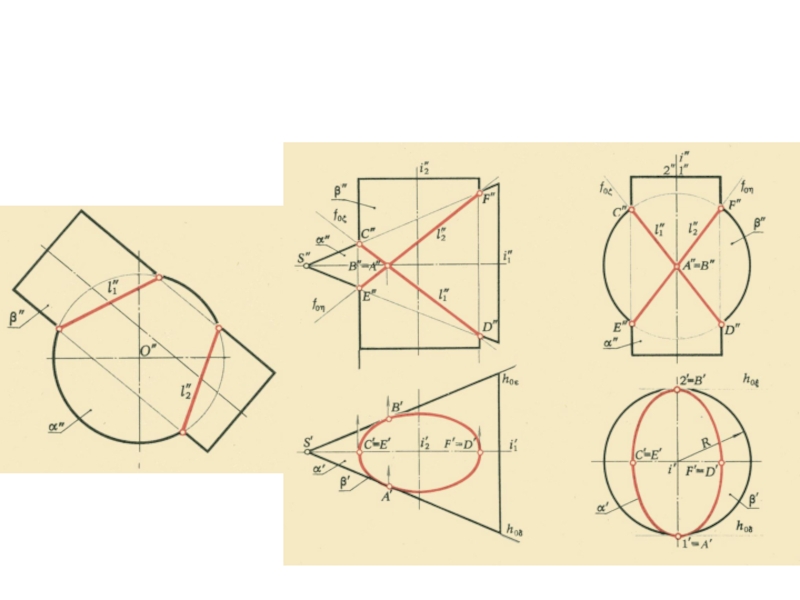
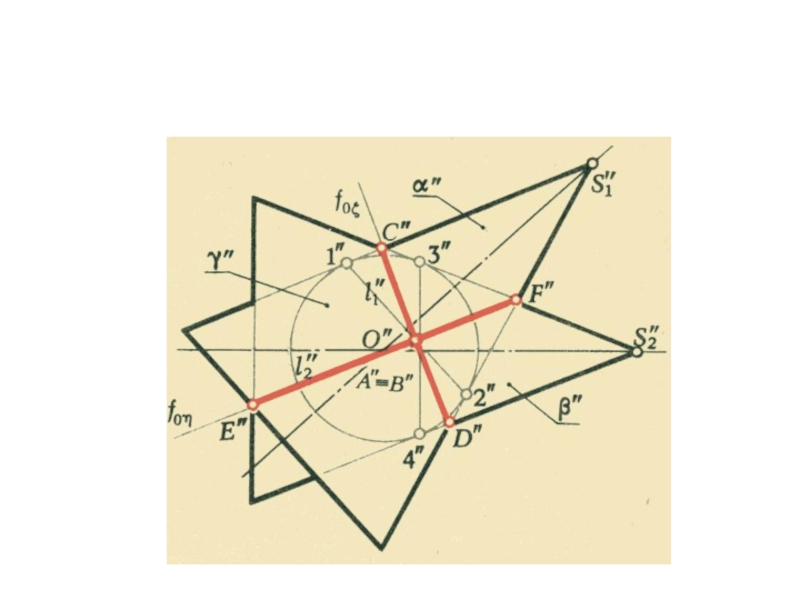
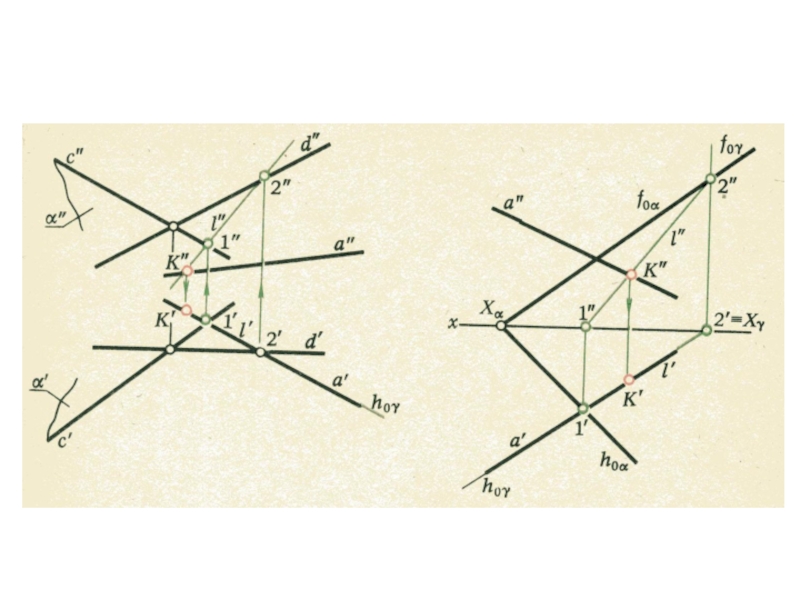
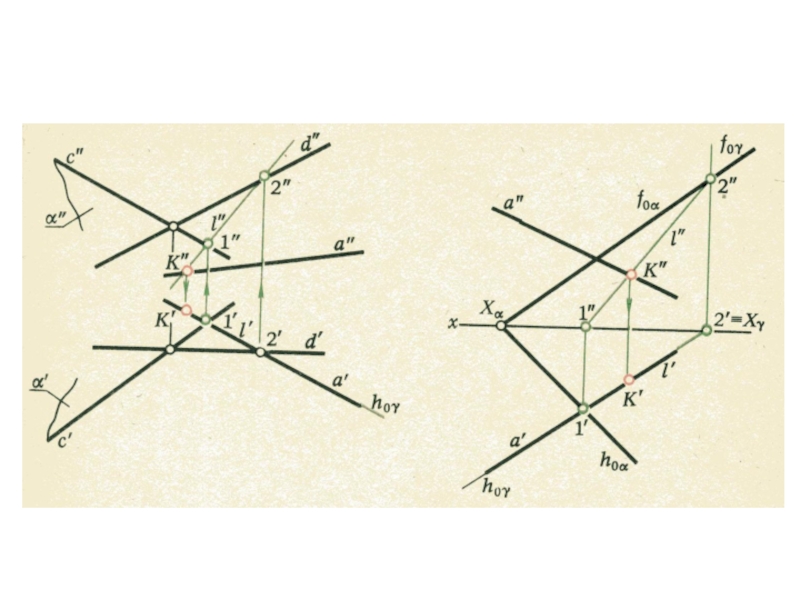
- 21. Пересечение плоскостей
- 22. Пересечение плоскостей
- 23. Пересечение плоскостей
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Плоскость, касательная к поверхности в заданной на
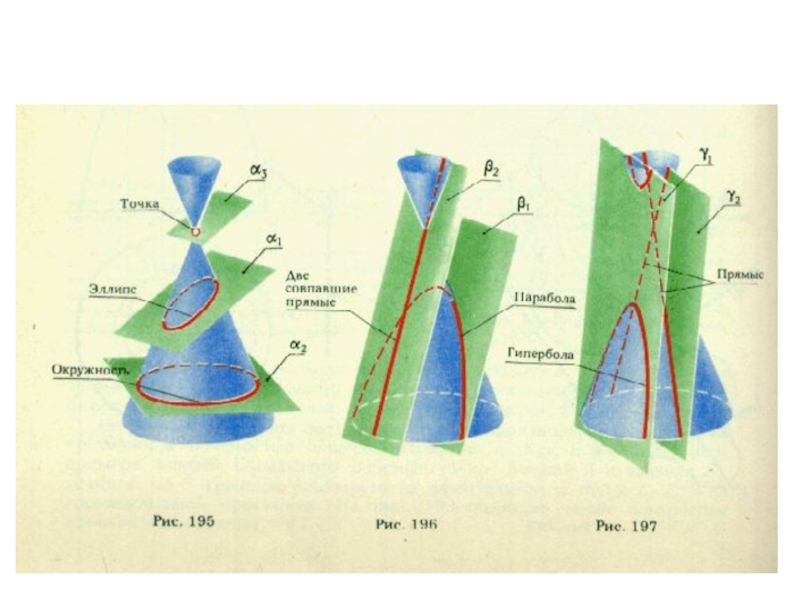
- 52. Индикатрисы Дюпена (1784-1873)Если индикатриса поверхности – эллипс,
- 53. Если касательная плоскость касается попрямой образующей, то
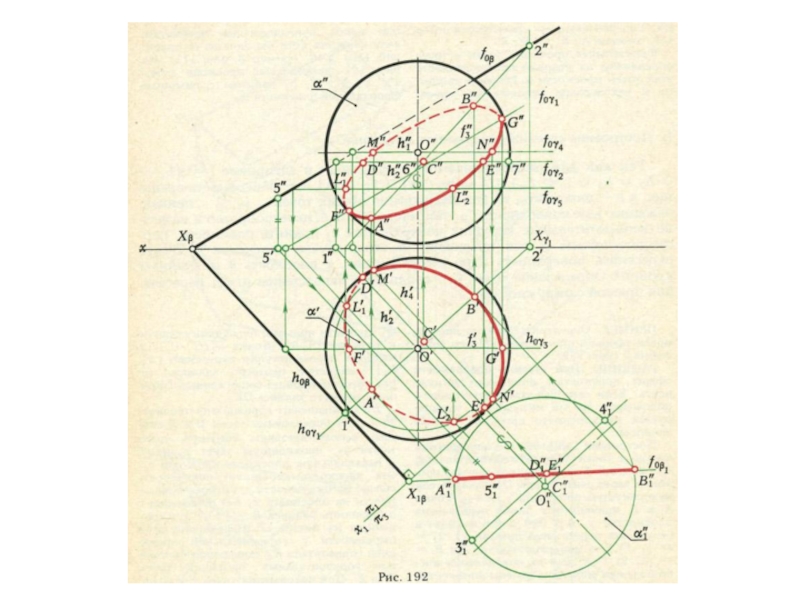
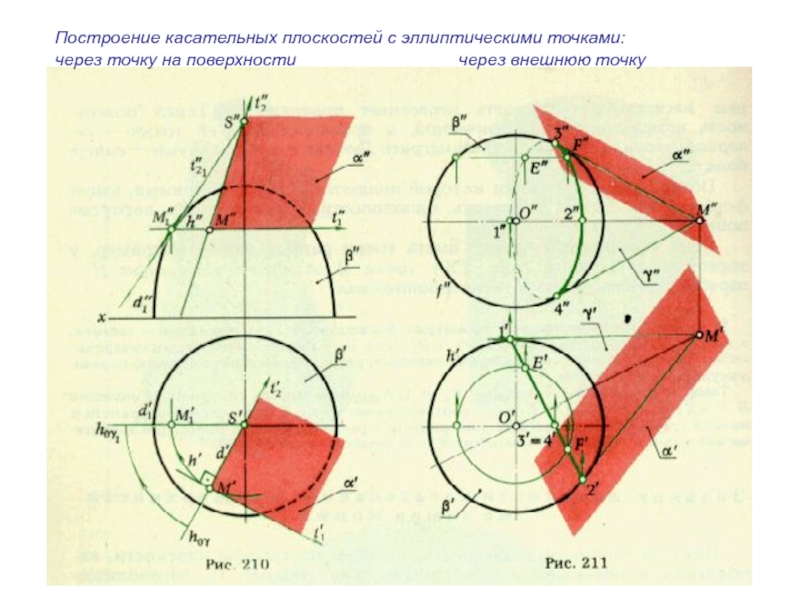
- 54. Построение касательных плоскостей с эллиптическими точками:через точку
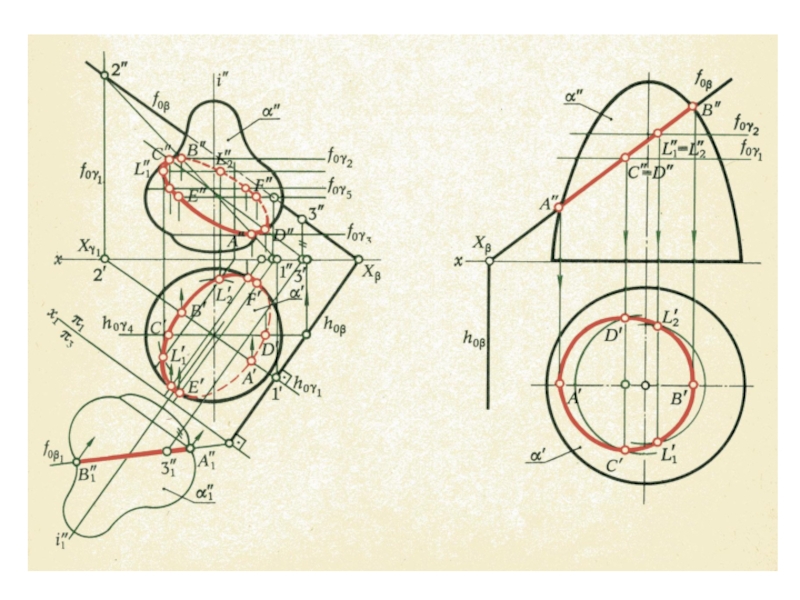
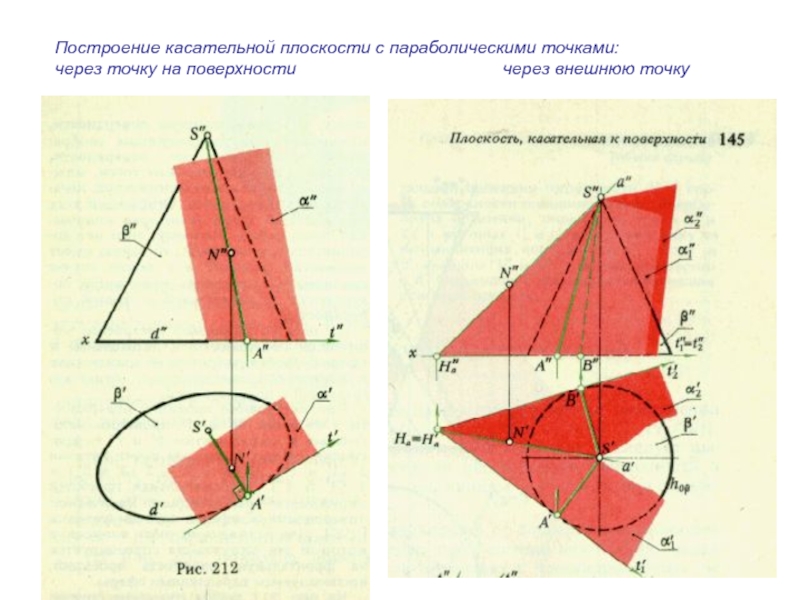
- 55. Построение касательной плоскости с параболическими точками:через точку
- 56. Построение касательной плоскости с гиперболическими точками
- 57. Слайд 57
- 58. Слайд 58
- 59. Слайд 59
- 60. Слайд 60
- 61. Слайд 61
- 62. Слайд 62
- 63. Слайд 63
- 64. Скачать презентанцию
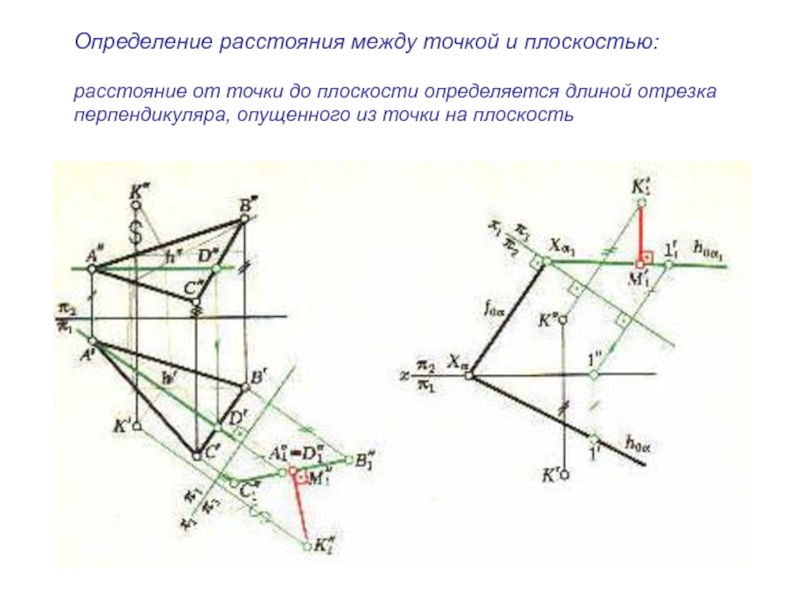
Определение расстояния между точкой и плоскостью:расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на плоскость
Слайды и текст этой презентации
Слайд 2Определение расстояния между точкой и плоскостью:
расстояние от точки до плоскости
определяется длиной отрезка
перпендикуляра, опущенного из точки на плоскость
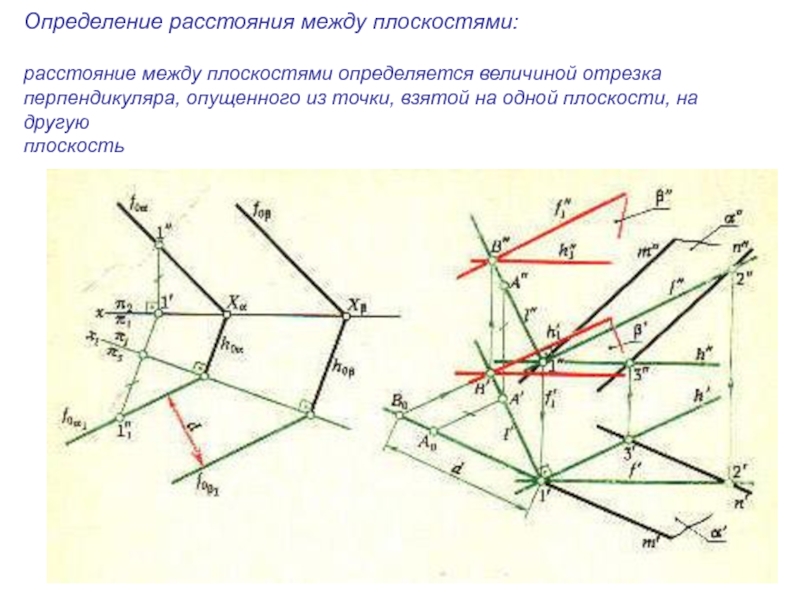
Слайд 3Определение расстояния между плоскостями:
расстояние между плоскостями определяется величиной отрезка
перпендикуляра, опущенного
из точки, взятой на одной плоскости, на другую
плоскость
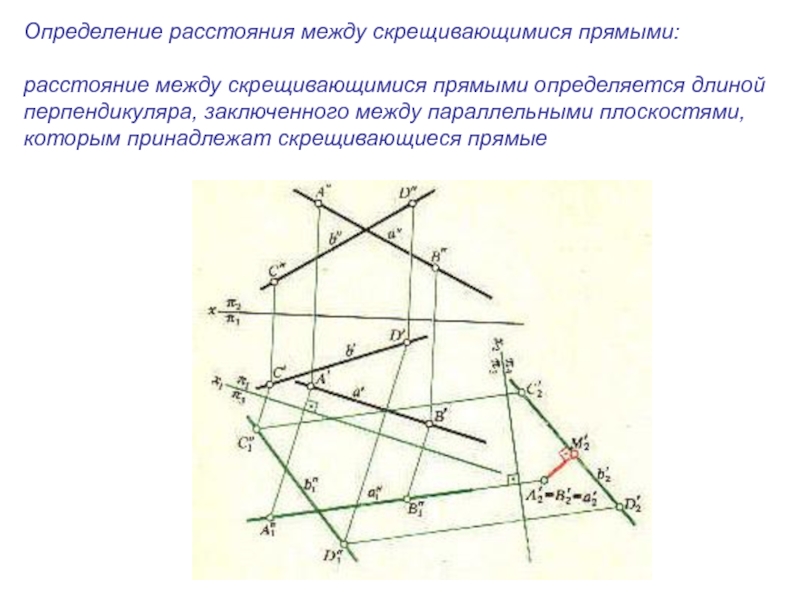
Слайд 4Определение расстояния между скрещивающимися прямыми:
расстояние между скрещивающимися прямыми определяется длиной
перпендикуляра,
заключенного между параллельными плоскостями,
которым принадлежат скрещивающиеся прямые
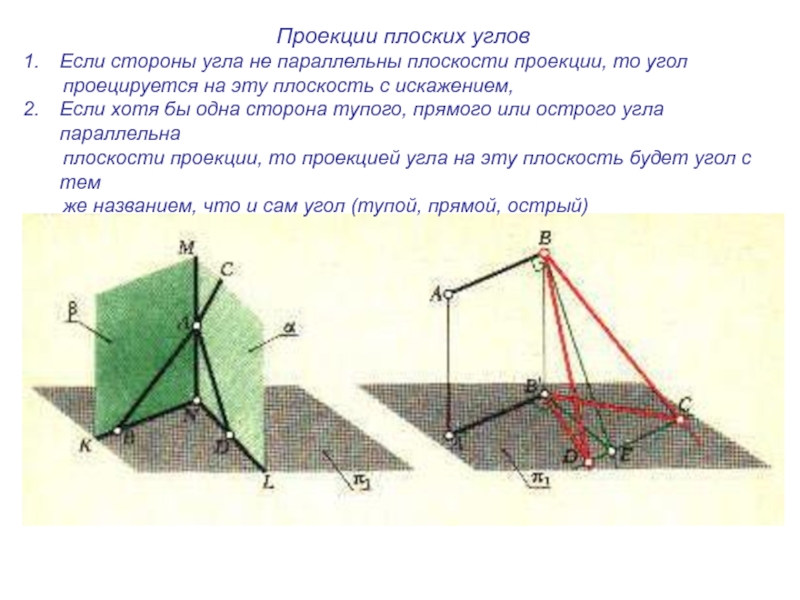
Слайд 5Проекции плоских углов
Если стороны угла не параллельны плоскости проекции, то
угол
проецируется на эту плоскость с искажением,
Если хотя
бы одна сторона тупого, прямого или острого угла параллельнаплоскости проекции, то проекцией угла на эту плоскость будет угол с тем
же названием, что и сам угол (тупой, прямой, острый)
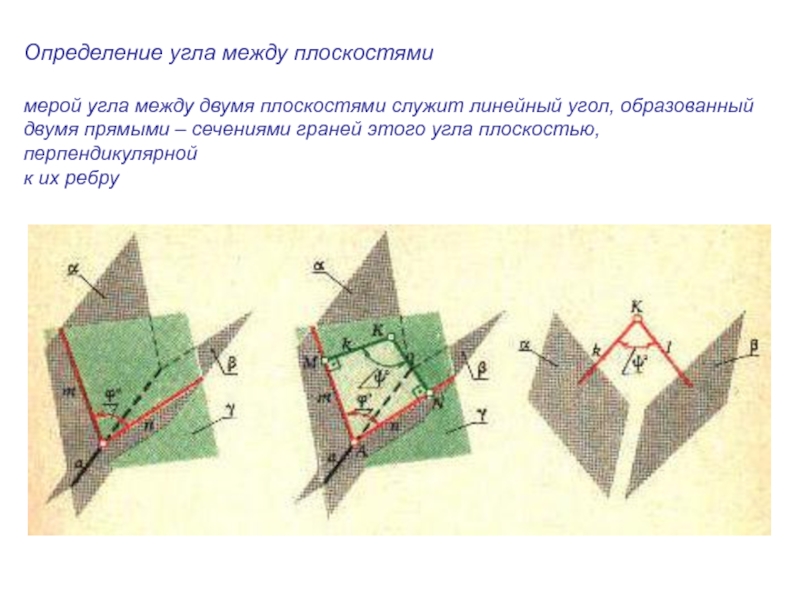
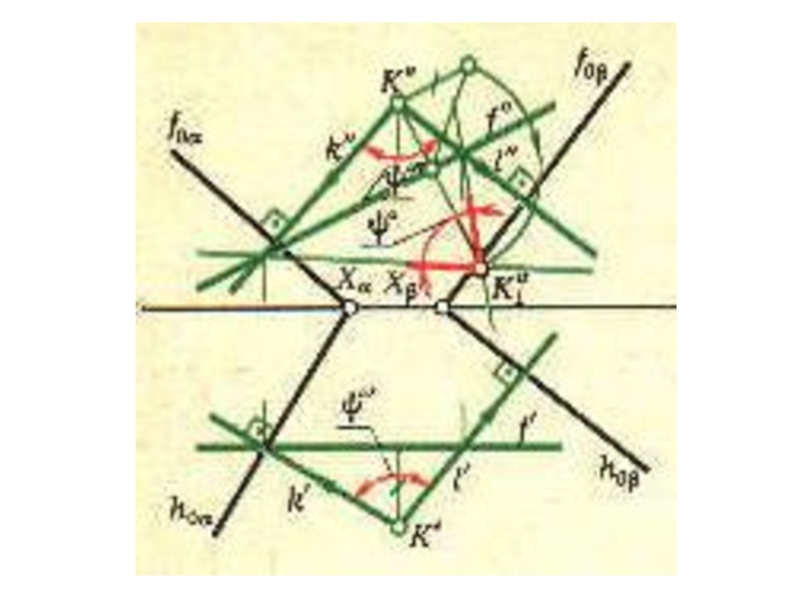
Слайд 8Определение угла между плоскостями
мерой угла между двумя плоскостями служит линейный
угол, образованный
двумя прямыми – сечениями граней этого угла плоскостью, перпендикулярной
к
их ребру
Слайд 11Определение угла между скрещивающимися прямыми
угол между скрещивающимися прямыми называется угол,
который
образуется между прямыми, проведенными из произвольной точки
пространства параллельно данным скрещивающимся
прямыми
Слайд 12Позиционные задачи
задачи на принадлежность:
принадлежность точки линии,
принадлежность точки поверхности,
принадлежность линии поверхности.
задачи
на пересечение:
пересечение линии с линией,
пересечение поверхностей,
пересечение линии с поверхностью.
К позиционным
относятся задачи, решение которых в конечном счете, сводится:- к построению точки принадлежащей линии,
- к построению точки, принадлежащей поверхности.
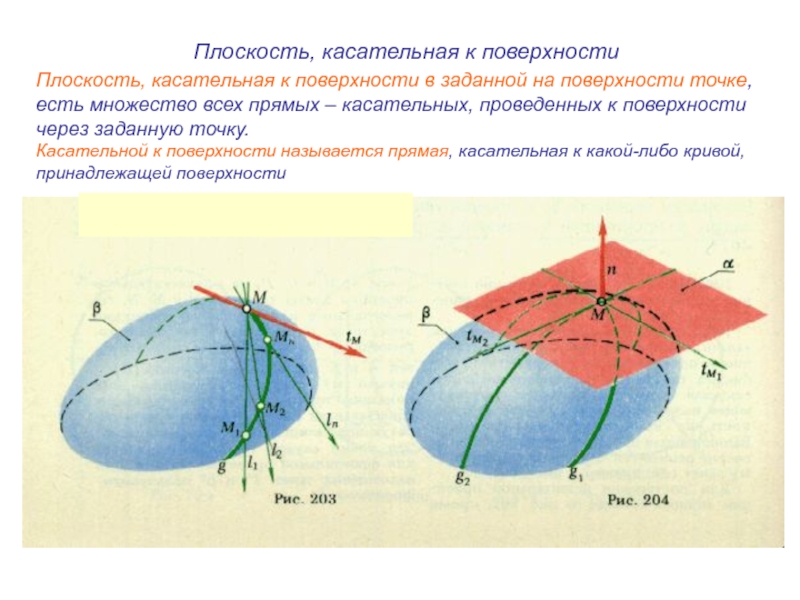
Слайд 51Плоскость, касательная к поверхности в заданной на поверхности точке,
есть
множество всех прямых – касательных, проведенных к поверхности
через заданную
точку.Касательной к поверхности называется прямая, касательная к какой-либо кривой,
принадлежащей поверхности
Плоскость, касательная к поверхности
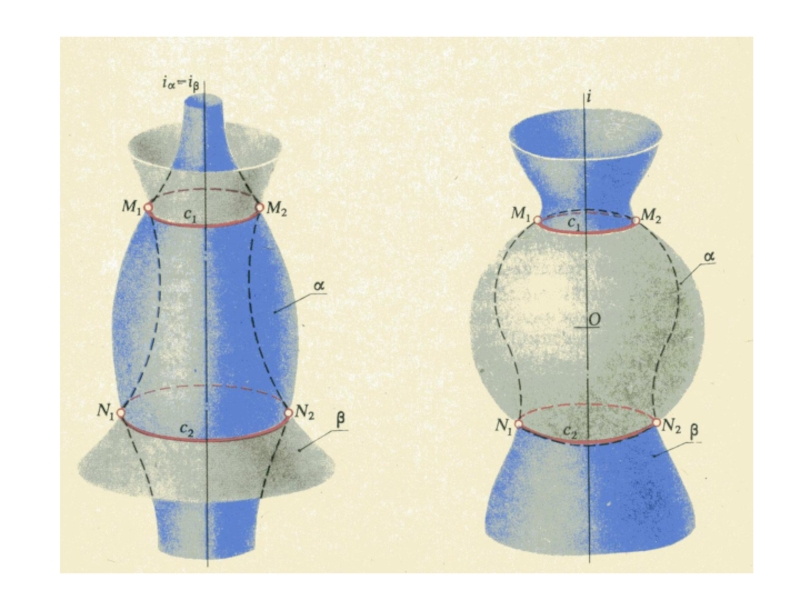
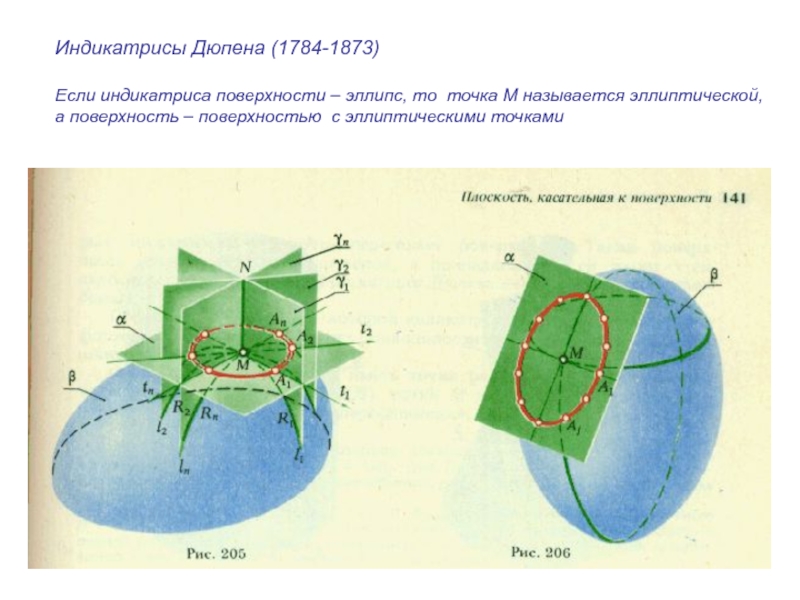
Слайд 52Индикатрисы Дюпена (1784-1873)
Если индикатриса поверхности – эллипс, то точка М
называется эллиптической,
а поверхность – поверхностью с эллиптическими точками
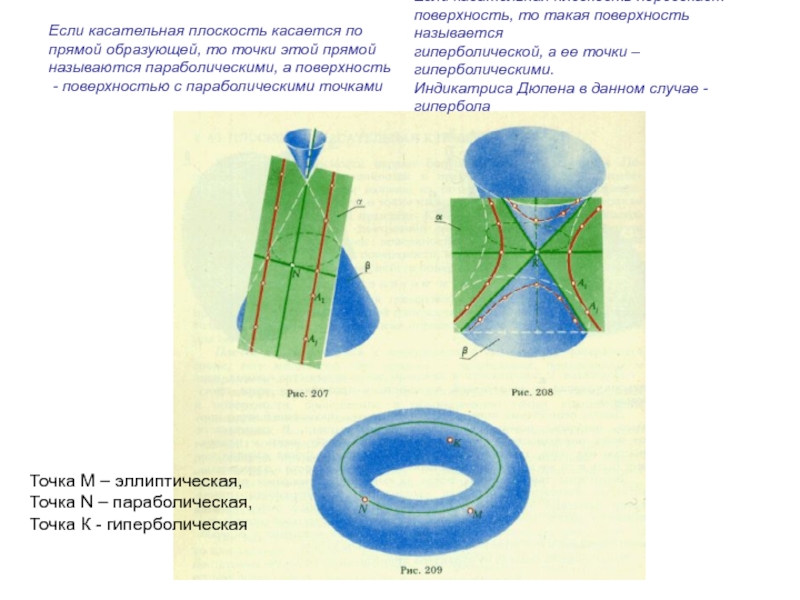
Слайд 53Если касательная плоскость касается по
прямой образующей, то точки этой прямой
называются
параболическими, а поверхность
- поверхностью с параболическими точками
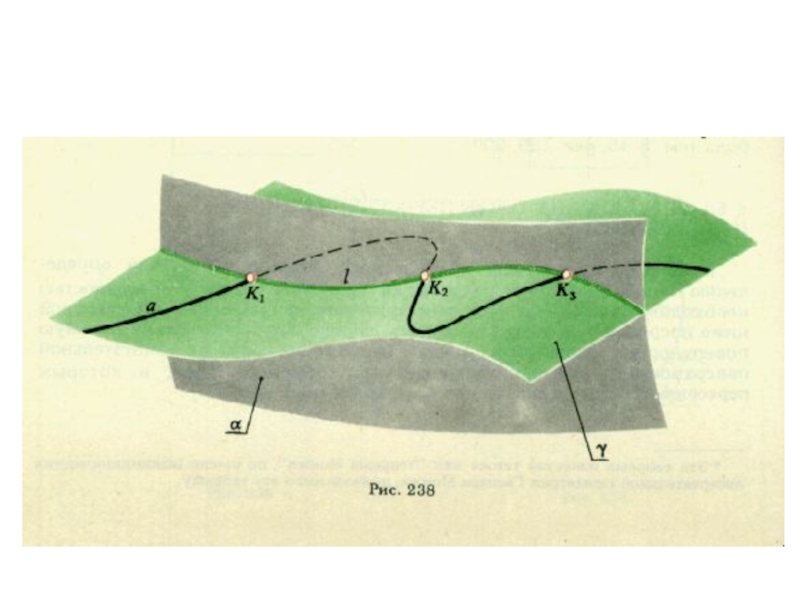
Если касательная плоскость
пересекаетповерхность, то такая поверхность называется
гиперболической, а ее точки – гиперболическими.
Индикатриса Дюпена в данном случае - гипербола
Точка М – эллиптическая,
Точка N – параболическая,
Точка К - гиперболическая
Слайд 54Построение касательных плоскостей с эллиптическими точками:
через точку на поверхности
через внешнюю точку
Слайд 55Построение касательной плоскости с параболическими точками:
через точку на поверхности
через внешнюю точку
