Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение линейного программирования в математических моделях
Содержание
- 1. Применение линейного программирования в математических моделях
- 2. /23ЛитератураЭкономико-математические методы и прикладные модели: Учеб. пособие
- 3. Известные ученые-экономистыЛеонид Витальевич Канторович родился 19 января
- 4. /233.1. Принцип оптимальности в планировании и управленииПринцип
- 5. Задачи линейного программированияВозможные области применения задач ЛП:рациональное
- 6. /233.2. Задача линейного программированияЭто развёрнутая форма записиЛинейная
- 7. /233.2. Задача линейного программированияЭто каноническая форма записиЛинейная
- 8. /233.2. Задача линейного программированияЭто матричная форма записиОна
- 9. /233.2. Задача линейного программированияЭто стандартная форма записиЛинейная
- 10. /233.2.Любой вектор x, удовлетворяющий ограничениям и условиям
- 11. Линейное программированиеПриведенный план местности изображает возвышенность с
- 12. Линейное программированиеНайти самую высокую точку областиX принадлежит
- 13. /233.2.ЗЛП может:не иметь ни одного оптимального решениядопустимой
- 14. /233.2.z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1 ≥
- 15. /233.2.z = max(x1+x2|0.1x1+0.1x2 ≤ 5, x1 ≥
- 16. /233.2.z = max(x1+x2|x1+5x2 ≤ 1, x1+x2 ≥
- 17. /233.2.z = max(2x1+x2|0.1x1+0.1x2 ≥ 5, x1 ≥
- 18. Геометрический смысл задачи линейного программирования
- 19. Задача о диете Составить задачу ЛП, позволяющую
- 20. Задача о диете Задача ЛПЗадача ЛП в канонической форме!
- 21. Задача о диете В 1982 г. Джорджу
- 22. Задача о диете=Задача о смесиНайти самую дешевую допустимую смесь.
- 23. /233.3. Симплексный методОграничения ЗЛП в канонической форме
- 24. /233.3. Симплексный метод Подставляя в ЦФ
- 25. /233.3. Симплексный метод Геометрическая интерпретация.Аналитическому переходу от
- 26. /233.3. Симплексный методИсходные условия применения симплексного методаЗЛП
- 27. /233.3.z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤
- 28. Теория принятия решенийПетрГУ, А.П.Мощевикин, 2004 г.Симплекс-метод ЛПЗапись
- 29. /233.3.z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤
- 30. /23В таблице выделены жирным шрифтом3.3.Разрешающий столбец:столбец с
- 31. /233.3.Выполняем обыкновенные жордановы исключения во всей таблице:для
- 32. Симплексный метод
- 33. Каноническая форма:max 20+3x2-x4x3 = 3 -0.4x1+0.1x4 x1=
- 34. Отрицательных cj больше нет – достигнут оптимум
- 35. /233.3.z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤
- 36. /233.3. Симплексный методИсходные условия применения симплексного методаЗЛП
- 37. /233.3. Симплексный методВывод:Не всякая задача ЛП может
- 38. /233.3. Симплексный методОпределение:Говорят, что ограничение задачи ЛП,
- 39. /233.3.1. случай:система ограничений имеет видПрименение линейного программирования
- 40. /233.3.2. случай:система ограничений имеет вид(напр. Задача о
- 41. /233.3.метод искусственного базисавводится искусственный базис:1. К левым
- 42. /233.3.Метод искусственного базиса, .Теорема 2. Если в
- 43. /233.3.Метод искусственного базисаПродолжение примера 1. Решение задачи
- 44. 3.3.Метод искусственного базиса, ., М-задача Применяем симплекс-метод,
- 45. /233.3.Метод искусственного базиса, ., М-задачаЦФ соответствуют две
- 46. /233.3.Метод искусственного базиса, ., М-задачаход решения М-задачи:с▲сначала
- 47. /233.3.Метод искусственного базиса, ., М-задачаЦФ соответствуют две строки!
- 48. /233.3.Метод искусственного базиса, ., М-задача
- 49. /233.3.Метод искусственного базиса, ., Решение М-задачи Решение исходной-задачи ЦФ после завершения итераций!!
- 50. /233.3.В некоторых случаях алгоритм симплексного метода может
- 51. ЗАДАЧА ОБ ОПТИМАЛЬНОМ РАСПРЕДЕЛЕНИИ РЕСУРСОВЗдесь (2.1) -
- 52. Двойственная задача Правила:Каждому i-му ограничению исходной задачи
- 53. Двойственная задача Правила:1. Каждому i-му ограничению исходной
- 54. Двойственная задача Теорема 1Пусть xj, j =
- 55. Свойства решений (следствия из теорем двойственности!)Значения целевых
- 56. /233.4. Экономические приложения линейного программированияМатрица потребности в
- 57. /233.4. Экономические приложения линейного программированияВектор цен продукции
- 58. Применение линейного программирования в математических моделях (с)
- 59. /233.5.Два способа установки XAЕсли есть права доступа
- 60. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1/23
Лекция 3. Применение линейного программирования в математических моделях
Содержание лекции:
Принцип оптимальности
в планировании и управлении
обеспечение линейного программированияСлайд 2/23
Литература
Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /
Под ред. В.В. Федосеева. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005.
— глава 2.Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001.
Канторович Л.В. Экономический расчёт наилучшего использования ресурсов. М.: Изд-во АН СССР, 1960.
Линейное программирование. Оптимальное распределение ресурсов. Методические указания для выполнения лабораторных работ для студентов направлений подготовки бакалавриата 120700, 080100 и 080200./НМСУ «Горный». Сост. В.В. Беляев, Т.Р. Косовцева. СПб, 2012., 62 с.
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 3Известные ученые-экономисты
Леонид Витальевич Канторович родился 19 января 1912г. в Санкт-Петербурге
в семье врача. В 18 лет он закончил математико-механический факультет
Ленинградского университета (1930) и уже через четыре года получил звание профессора. Л.В.Канторович является одним из основателей отечественных школ функционального анализа. вычислительной математики, языков программирования.С 1938г. интересы Л.В.Канторовича были неразрывно связаны с экономическими исследованиями и решением народнохозяйственных проблем.
Крупнейшим его открытием является введение в математическую и экономическую науки понятия "линейное программирование" (1939). Линейное программирование является универсальной математической моделью оптимального функционирования экономических систем. Основная заслуга Л.В.Канторовича заключается в разработке единого подхода к широкому кругу экономических задач о наилучшем использовании ресурсов на базе линейного программирования.
Слайд 4/23
3.1. Принцип оптимальности в планировании и управлении
Принцип оптимальности предполагает следующее:
наличие
определённых ресурсов
наличие определённых технологических возможностей
цель хозяйственной деятельности
извлечение прибыли
удовлетворение потребностей
предотвращение угрозы
накопление
знанийи т.д.
Суть принципа:
планировать хозяйственную деятельность таким образом, чтобы при имеющихся ресурсах и технологиях не существовало способа достичь цели в большей степени, чем это предусматривает план
В полной мере этот принцип может быть реализован только с помощью экономико-математических моделей
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 5Задачи линейного программирования
Возможные области применения задач ЛП:
рациональное использование сырья и
материалов;
задачи составления смесей;
задачи оптимизации раскроя;
оптимизации производственной программы предприятий;
оптимального размещения и
концентрации производства; на составление оптимального плана перевозок, работы транспорта;
задача о назначениях;
управления производственными запасами;
и многие другие, принадлежащие сфере оптимального планирования.
Слайд 6/23
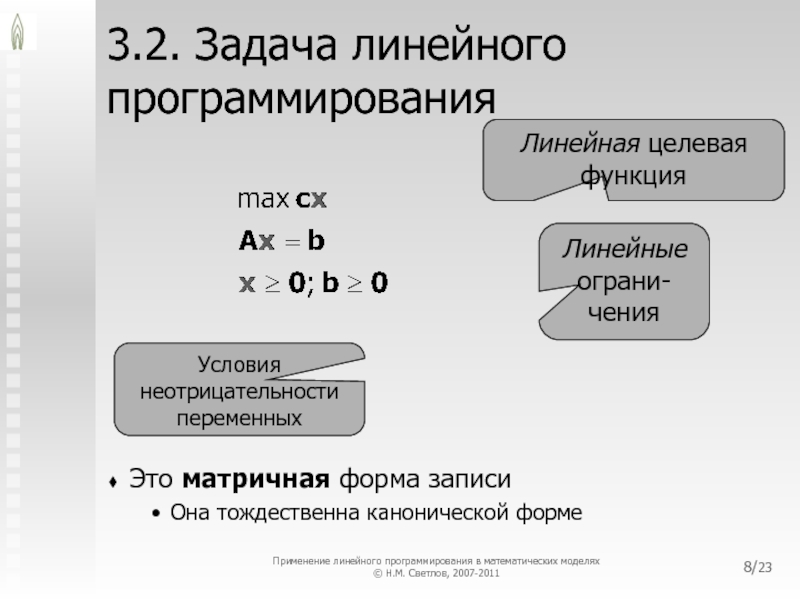
3.2. Задача линейного программирования
Это развёрнутая форма записи
Линейная целевая функция
Линейные ограни-чения
Условия
неотрицательности переменных
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 7/23
3.2. Задача линейного программирования
Это каноническая форма записи
Линейная целевая функция (ЦФ)
Линейные
ограни-чения
(фазовые ограничения)
Условия неотрицательности переменных (естественные ограничения)
Любую ЗЛП можно записать в
каноническом виде (ограничения – равенства, свободные члены неотрицательны, решается на максимум)
Слайд 8/23
3.2. Задача линейного программирования
Это матричная форма записи
Она тождественна канонической форме
Линейная
целевая функция
Линейные ограни-чения
Условия неотрицательности переменных
Применение линейного программирования в математических моделях
©
Н.М. Светлов, 2007-2011Слайд 9/23
3.2. Задача линейного программирования
Это стандартная форма записи
Линейная целевая функция
Линейные ограни-чения
Условия
неотрицательности переменных
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 10/23
3.2.
Любой вектор x, удовлетворяющий ограничениям и условиям неотрицательности (безотносительно к
целевой функции), называется допустимым решением
Если допустимых решений не существует, говорят,
что система ограничений несовместнаОбластью допустимых решений (ОДР) называется множество, включающее все допустимые решения данной ЗЛП
Допустимое решение x*, доставляющее наибольшее значение целевой функции среди всех допустимых решений данной ЗЛП, называется оптимальным решением
часто его называют просто решением ЗЛП
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 11Линейное программирование
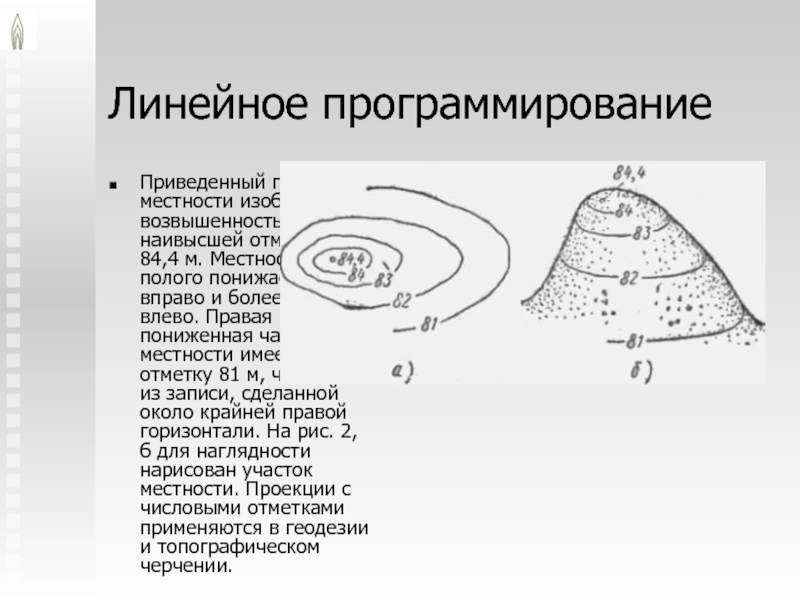
Приведенный план местности изображает возвышенность с наивысшей отметкой 84,4
м. Местность полого понижается вправо и более круто влево. Правая
пониженная часть местности имеет отметку 81 м, что видно из записи, сделанной около крайней правой горизонтали. На рис. 2, б для наглядности нарисован участок местности. Проекции с числовыми отметками применяются в геодезии и топографическом черчении.Слайд 12Линейное программирование
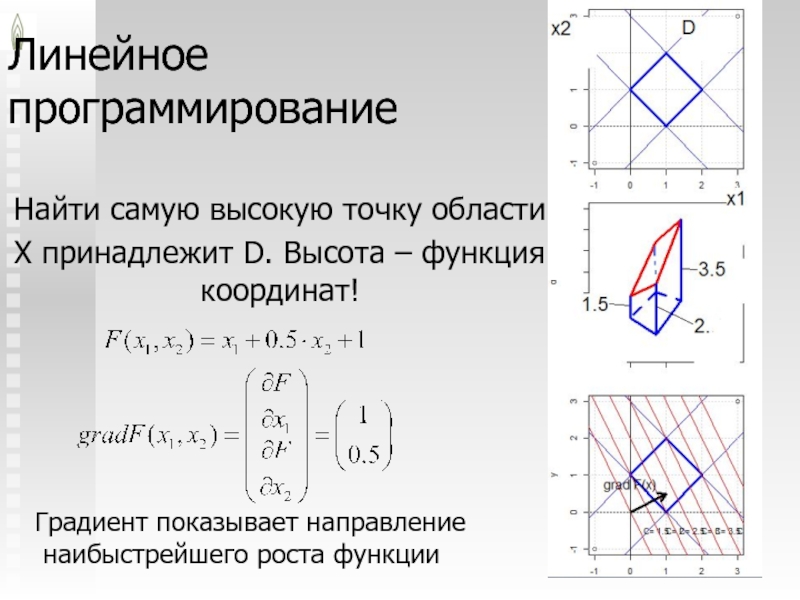
Найти самую высокую точку области
X принадлежит D. Высота –
функция координат!
Градиент показывает направление
наибыстрейшего роста функции
Слайд 13/23
3.2.
ЗЛП может:
не иметь ни одного оптимального решения
допустимой области не существует
– система ограничений не совместна
z = max(x1+x2|x1+5x2 ≤ 1, x1+x2
≥ 5, x1 ≥ 0, x2 ≥ 0)допустимая область существует, но не ограничивает целевую функцию
z = max(2x1+x2|0.1x1+0.1x2 ≥ 5, x1 ≥ 0, x2 ≥ 0)
иметь одно оптимальное решение
z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1 ≥ 0, x2 ≥ 0)
x1=50, x2 =0; z = 50
иметь бесконечно много оптимальных решений
z = max(x1+x2|0.1x1+0.1x2 ≤ 5, x1 ≥ 0, x2 ≥ 0)
x1=50, x2 =0; z = 50 … x1=0, x2 =50; z = 50
Компактная запись
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 14/23
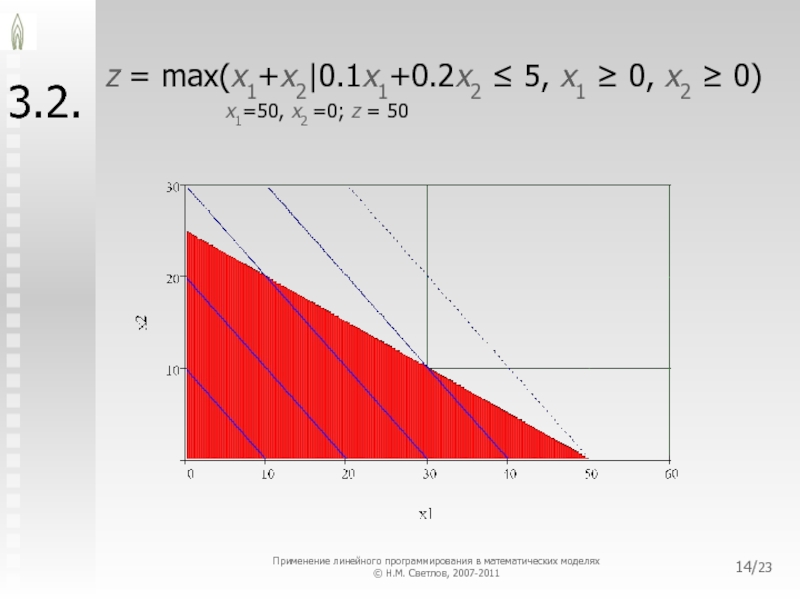
3.2.
z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1 ≥ 0, x2 ≥
0)
x1=50, x2 =0; z = 50
Применение линейного программирования в
математических моделях
© Н.М. Светлов, 2007-2011Слайд 15/23
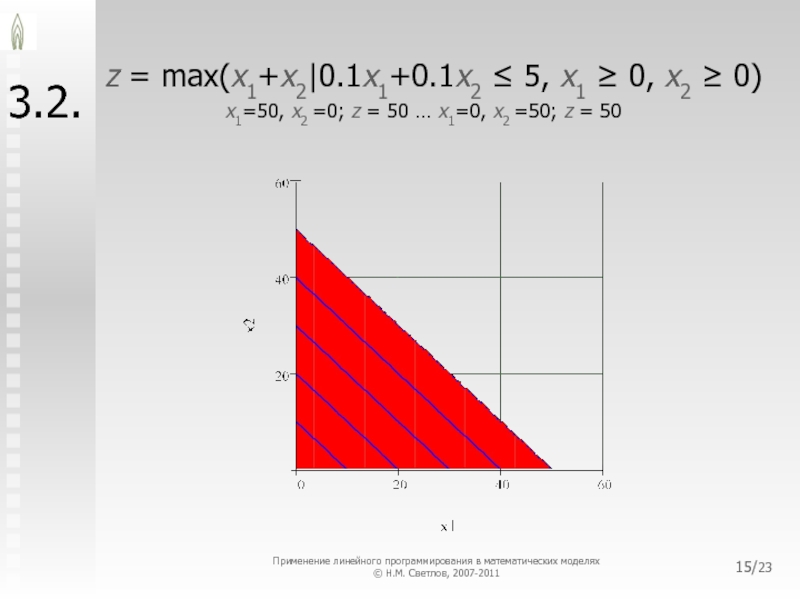
3.2.
z = max(x1+x2|0.1x1+0.1x2 ≤ 5, x1 ≥ 0, x2 ≥
0)
x1=50, x2 =0; z = 50 … x1=0, x2
=50; z = 50Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 16/23
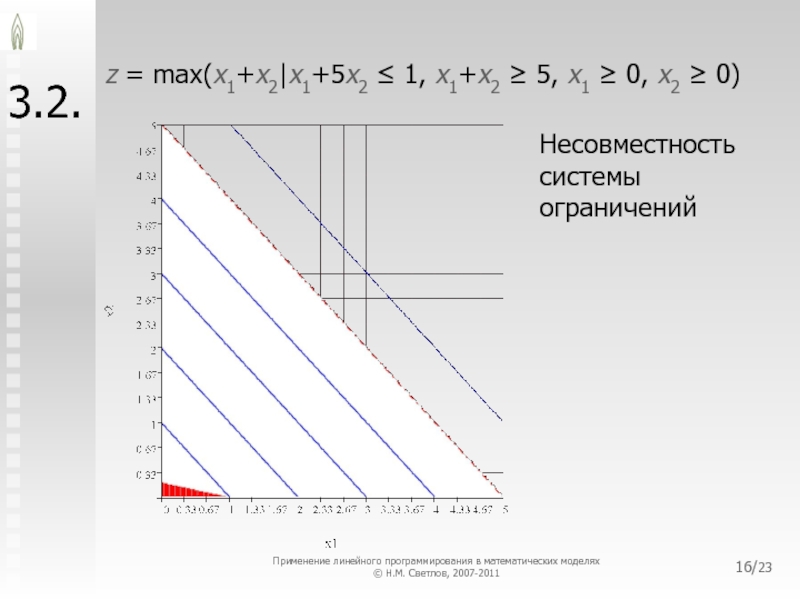
3.2.
z = max(x1+x2|x1+5x2 ≤ 1, x1+x2 ≥ 5, x1 ≥
0, x2 ≥ 0)
Несовместность системы ограничений
Применение линейного программирования в математических
моделях
© Н.М. Светлов, 2007-2011Слайд 17/23
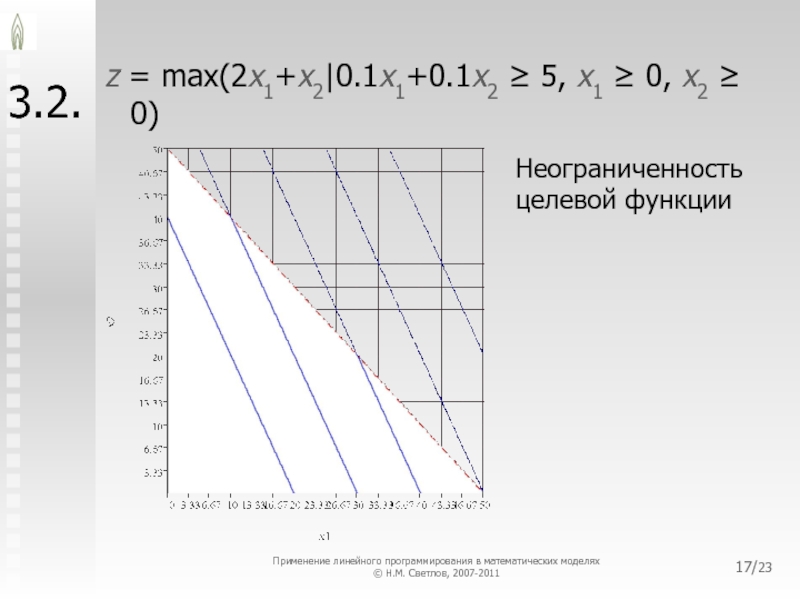
3.2.
z = max(2x1+x2|0.1x1+0.1x2 ≥ 5, x1 ≥ 0, x2 ≥
0)
Неограниченность целевой функции
Применение линейного программирования в математических моделях
© Н.М. Светлов,
2007-2011Слайд 19Задача о диете
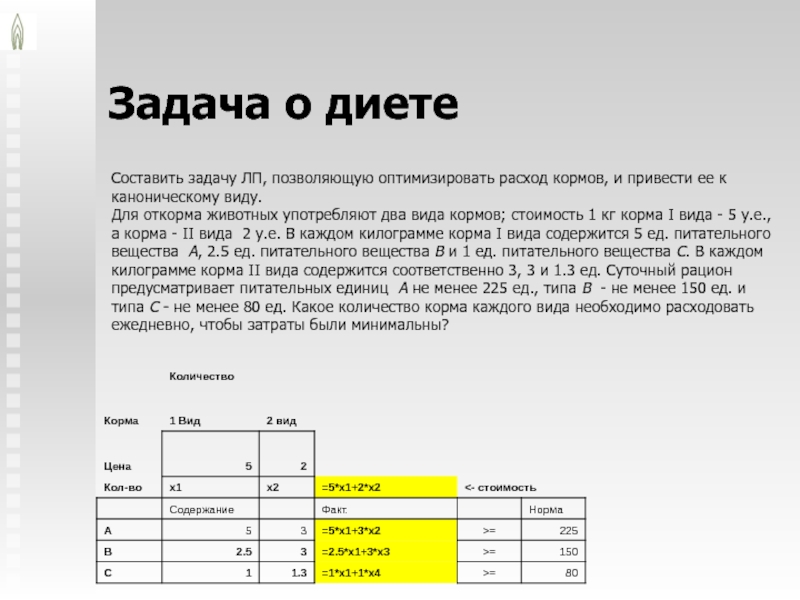
Составить задачу ЛП, позволяющую оптимизировать расход кормов,
и привести ее к каноническому виду.
Для откорма животных употребляют два
вида кормов; стоимость 1 кг корма I вида - 5 у.е., а корма - II вида 2 у.е. В каждом килограмме корма I вида содержится 5 ед. питательного вещества А, 2.5 ед. питательного вещества B и 1 ед. питательного вещества C. В каждом килограмме корма II вида содержится соответственно 3, 3 и 1.3 ед. Суточный рацион предусматривает питательных единиц A не менее 225 ед., типа B - не менее 150 ед. и типа C - не менее 80 ед. Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты были минимальны?Слайд 21Задача о диете
В 1982 г. Джорджу Стиглеру была присуждена
Нобелевская премия за труды по теории экономического регулирования (совсем не
проблемы линейного программирования!)Еще в 1945 г. без помощи линейного программирования ДЖОРДЖ СТИГЛЕР. составил "самый дешевый набор продуктов", явившийся фактически прообразом потребительской корзины.
Пытался найти наиболее дешевый рацион, удовлетворяющий 9 диетическим требования, сформулированным в 1943 году. В наборе продуктов было 77 наименований, от пшеничной муки до клубничного джема.
Подводя итоги своей работы в 1945 «Затраты на питание» :
«По всей видимости не существует универсального метода нахождения минимума линейной функции при «соблюдении линейных ограничений.
Разработав в конце 40-х годов симплекс-метод, Георг Данциг совершил переворот. 70 лет назад решение задачи составления рациона вызывало затруднения у лучших экономистов мира, теперь доступно для начинающих студентов.
Слайд 23/23
3.3. Симплексный метод
Ограничения ЗЛП в канонической форме приводятся к виду
Переменные (неизвестные)
называются базисными, а весь набор
– базисом, остальные переменные называются свободными. Базисное решение называется допустимым, если оно неотрицательно.
Система ограничений (*) называется системой приведенной к единичному базису.
Отметим важнейшие условия наличия единичного базиса:
от каждого уравнения в него входит одна и только одна неизвестная;
каждая переменная из этого набора входит с коэффициентом +1 и отсутствует в остальных уравнениях;
все значения bi >=0
(*)
Основная идея симплекс-метода
Слайд 24/23
3.3. Симплексный метод
Подставляя в ЦФ вместо базисных переменных
их выражения через свободные переменные из системы
Полагая все свободные переменные
равными нулю, найдем значения базисных переменных . Получим Если все значения bi >=0, то набор является допустимым решением ЗЛП.
Такое допустимое решение называется базисным или опорным
Значение ЦФ при этом равно F=c0
(**)
Основная идея симплекс-метода
Основная идея симплекс-метода. Решение задачи при помощи симплекс-метода подразумевает ряд шагов, состоящих в том, что от данного базиса B’ переходим к другому базису B’’ с таким расчетом, чтобы значение целевой функции F увеличивалось или, по крайней мере, не уменьшалось.FB’<=FB’’
Слайд 25/23
3.3. Симплексный метод
Геометрическая интерпретация.
Аналитическому переходу от одного базиса к
другому соответствует переход от одной вершины многогранника (множества допустимых решений)
к другой, в которой целевая функция имеет не меньшее значение. Этот факт основан на том, что вершинам многоугольника множества допустимых решений соответствуют базисные решения системы ограничений.Основная идея симплекс-метода
Слайд 26/23
3.3. Симплексный метод
Исходные условия применения симплексного метода
ЗЛП записана в канонической
форме
Её ограничения линейно независимы
Известно опорное решение, в котором:
имеется не
более m ненулевых переменныхзадача содержит n переменных и m ограничений
все ограничения выполняются (область D не пуста!)
m переменных, называемых базисными (среди которых все ненулевые)
выражены через:
n–m переменных, называемых свободными (каждая равна нулю)
свободный член ограничения bi положителен
Результат этой процедуры записан в начальную (первую, исходную) симплексную таблицу
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 27/23
3.3.
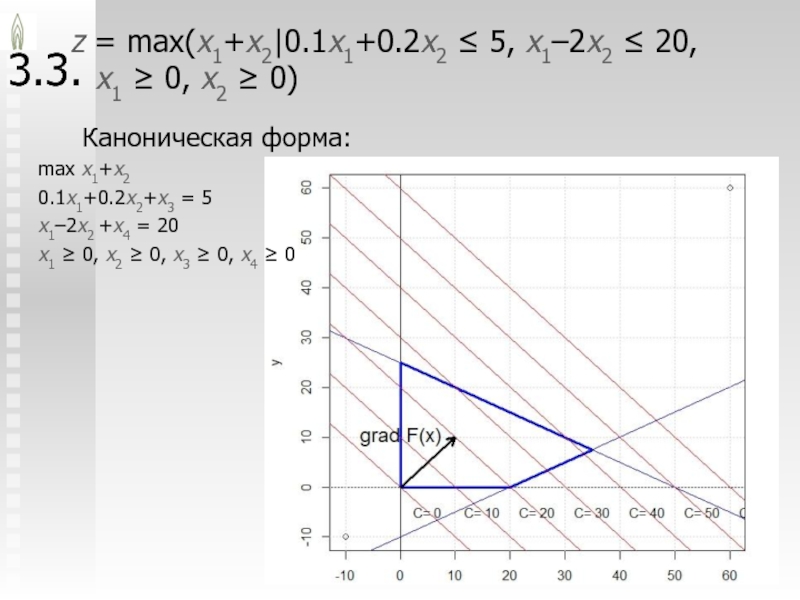
z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 20,
x1 ≥
0, x2 ≥ 0)
Каноническая форма:
max x1+x2
0.1x1+0.2x2+x3 = 5
x1–2x2 +x4
= 20x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
Слайд 28Теория принятия решений
ПетрГУ, А.П.Мощевикин, 2004 г.
Симплекс-метод ЛП
Запись задачи в виде
уравнений
x1 + a1,m+1xm+1 + ... + a1sxs+...+ a1nxn = b1;
x2
+ a2,m+1xm+1 + ... + a2sxs+...+ a2nxn = b2;...
xm + am,m+1xm+1 + ... + amsxs+...+ amnxn = bm.
тождественна записи в виде матриц
1 0 .. 0 a1,m+1 .. a1s .. a1n x1 b1
0 1 .. 0 a2,m+1 .. a2s .. a2n x2 = b2
. . .. . . .. . .. . .. ..
0 0 .. 1 am,m+1 .. ams .. amn xn bm
В симплекс-таблице будем записывать только коэффициенты матриц!
Слайд 29/23
3.3.
z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 20,
x1 ≥
0, x2 ≥ 0)
Каноническая форма:
max x1+x2
0.1x1+0.2x2+x3 = 5
x1–2x2 +x4
= 20x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
F=0-(-1* x1-1*x2)
x3 = 5- 0.1x1-0.2x2
x4 = 20- x1+2x2
F=0-(-1* x1-1*x2)=0
x3 = 5- 0.1x1-0.2x2 =5
x4 = 20- x1+2x2=20
Базисное решение (0, 0, 5, 20)
Смысл записей в симплекс-таблице:
Полагая x1 = 0, x2 = 0,
Слайд 30/23
В таблице
выделены
жирным
шрифтом
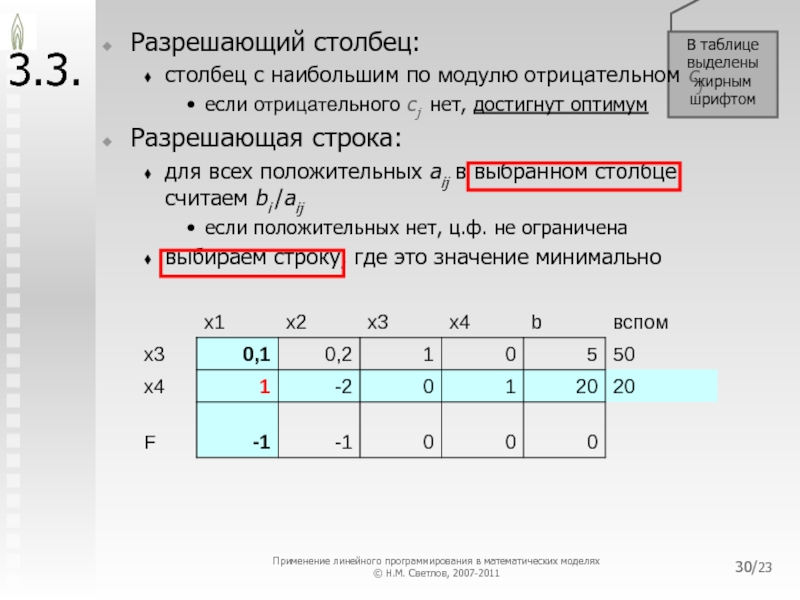
3.3.
Разрешающий столбец:
столбец с наибольшим по модулю отрицательном cj
если отрицательного
cj нет, достигнут оптимум
Разрешающая строка:
для всех положительных aij в выбранном
столбце
считаем bi /aijесли положительных нет, ц.ф. не ограничена
выбираем строку, где это значение минимально
Применение линейного программирования в математических моделях
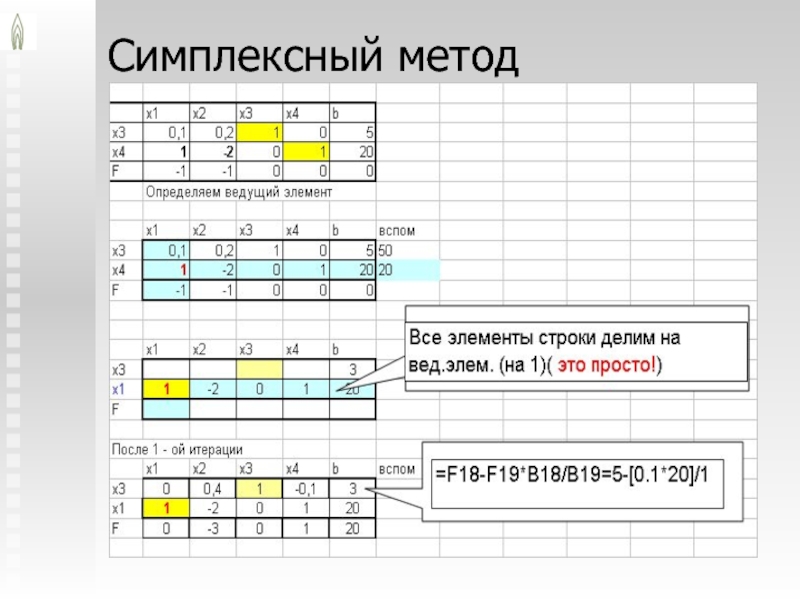
© Н.М. Светлов, 2007-2011
Слайд 31/23
3.3.
Выполняем обыкновенные жордановы исключения во всей таблице:
для строк i ≠i'
: aijнов = aij – ai'jaij' /ai'j' , где
i' и
j' – координаты ведущих (разрешающих) строки и столбцадля строки i =i' : aijнов = aij /ai'j'
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
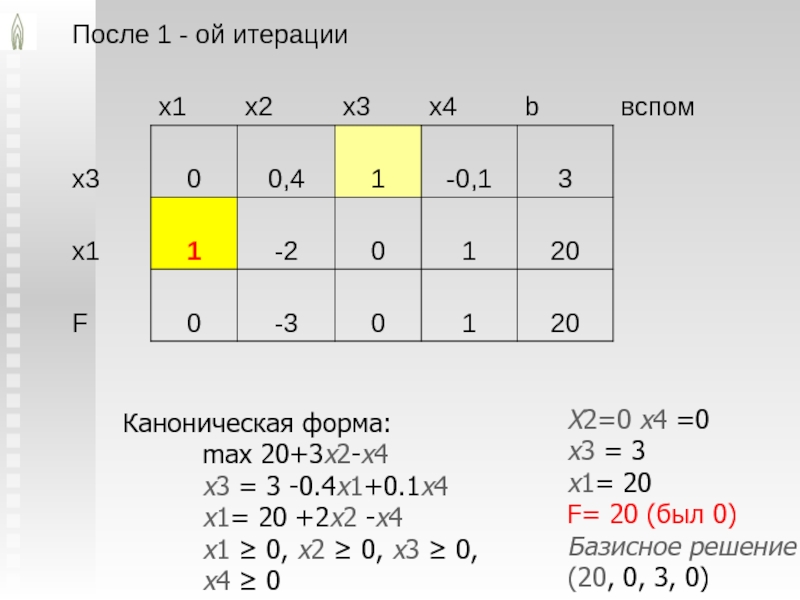
Слайд 33
Каноническая форма:
max 20+3x2-x4
x3 = 3 -0.4x1+0.1x4
x1= 20 +2x2 -x4
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4
≥ 0X2=0 x4 =0
x3 = 3
x1= 20
F= 20 (был 0)
Базисное решение (20, 0, 3, 0)
Слайд 34
Отрицательных cj больше нет
– достигнут оптимум
(в больших задачах
для этого требуются тысячи итераций)
Каноническая форма:
max 42.5-7.5x3-0.25x4
x2 = 7.5 -2.5x3-0.25x4
x1= 35 -5x3-0.5x4
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
X3=0 x4 =0
x2 = 7.5 -2.5x3-0.25x4 =7.5
x1= 35 -5x3-0.5x4 =35
F= 42.5-7.5x3-0.25x4=42.5
(было 20)
Базисное решение (35, 7.5, 0, 0) оптимальное!
Слайд 35/23
3.3.
z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 20,
x1 ≥
0, x2 ≥ 0)
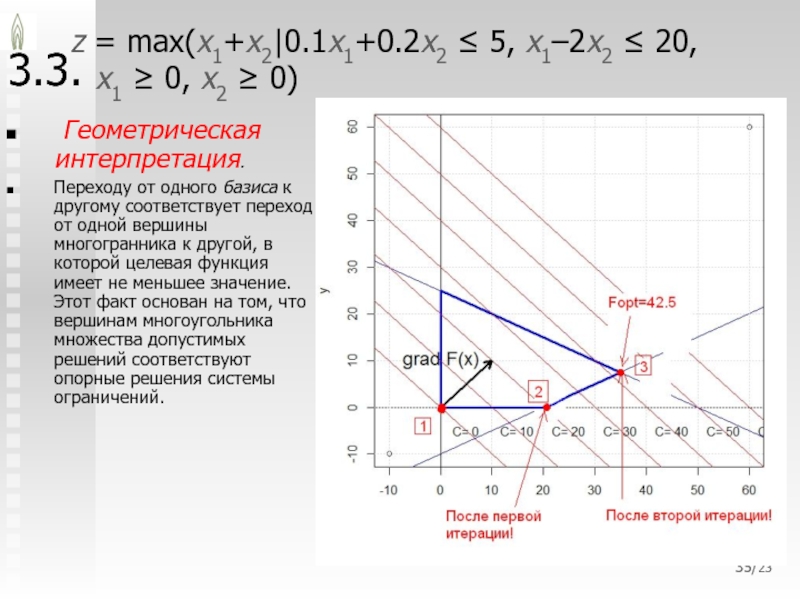
Геометрическая интерпретация.
Переходу от одного базиса
к другому соответствует переход от одной вершины многогранника к другой, в которой целевая функция имеет не меньшее значение. Этот факт основан на том, что вершинам многоугольника множества допустимых решений соответствуют опорные решения системы ограничений.Слайд 36/23
3.3. Симплексный метод
Исходные условия применения симплексного метода
ЗЛП записана в канонической
форме
Её ограничения линейно независимы
Известно опорное решение, в котором:
имеется не
более m ненулевых переменныхзадача содержит n переменных и m ограничений
все ограничения выполняются (область D не пуста!)
m переменных, называемых базисными (среди которых все ненулевые)
выражены через:
n–m переменных, называемых свободными (каждая равна нулю)
свободный член ограничения bi положителен
Результат этой процедуры записан в начальную (первую, исходную) симплексную таблицу
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 37/23
3.3. Симплексный метод
Вывод:
Не всякая задача ЛП может быть решена непосредственным
применением симплекс-метода. Для этого требуется, чтобы система фазовых ограничений содержала
единичный базис, а целевая функция была выражена через свободные переменные.Поэтому, в общем случае для решения задачи ЛП, после ее приведения к канонической форме необходимо приведение ограничений к единичному базису, это возможно когда фазовые ограничения имеют предпочтительный вид.
Слайд 38/23
3.3. Симплексный метод
Определение:
Говорят, что ограничение задачи ЛП, имеет предпочтительный вид,
если
при неотрицательной правой части (bi) левая часть ограничений содержит
переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.
Возможны два случая:
Слайд 39/23
3.3.
1. случай:
система ограничений имеет вид
Применение линейного программирования в математических моделях
©
Н.М. Светлов, 2007-2011
,
.
ОК!
В целевую функцию дополнительные переменные вводятся с
коэффициентами, равными нулю Слайд 40/23
3.3.
2. случай:
система ограничений имеет вид
(напр. Задача о диете)
Применение линейного программирования
в математических моделях
© Н.М. Светлов, 2007-2011
,
.
система ограничений не имеет
предпочтительного вида!ОК!
Слайд 41/23
3.3.
метод искусственного базиса
вводится искусственный базис:
1. К левым частям ограничений-равенств, не
имеющих предпочтительного вида, добавляют искусственные переменные
(вводится искусственный базис:)
,
.
ОК!
,
2.
В ЦФ искусственные переменные, вводят с коэффициентом -М, где М - большое положительное число.Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид!
Её начальный опорный план имеет вид!
Слайд 42/23
3.3.
Метод искусственного базиса
,
.
Теорема 2. Если в оптимальном плане М-задачи
хотя бы одна из искусственных переменных отлична от нуля, то
исходная задача не имеет допустимых планов, т. е. ее условия несовместны.,
все искусственные переменные .
Теорема 1.
Если в оптимальном плане М-задачи
, то план
является
оптимальным планом исходной задачи
Решение исходной задачи симплексным методом путем введения искусственных переменных называется симплексным методом с искусственным базисом
Слайд 43/23
3.3.
Метод искусственного базиса
Продолжение примера 1. Решение задачи о диете
,
.
,
М-задача в предпочтительном виде.
М - большое положительное число.
Выразим ЦФ через
свободные переменные Каноническая форма
Нет предпочтительного вида.
Слайд 443.3.
Метод искусственного базиса
,
.
,
М-задача
Применяем симплекс-метод, взяв в качестве
базисных переменных искусственные переменные, а в качестве свободных переменных -
Каноническая
форма!ЦФ через свободные переменные
Слайд 45/23
3.3.
Метод искусственного базиса
,
.
,
М-задача
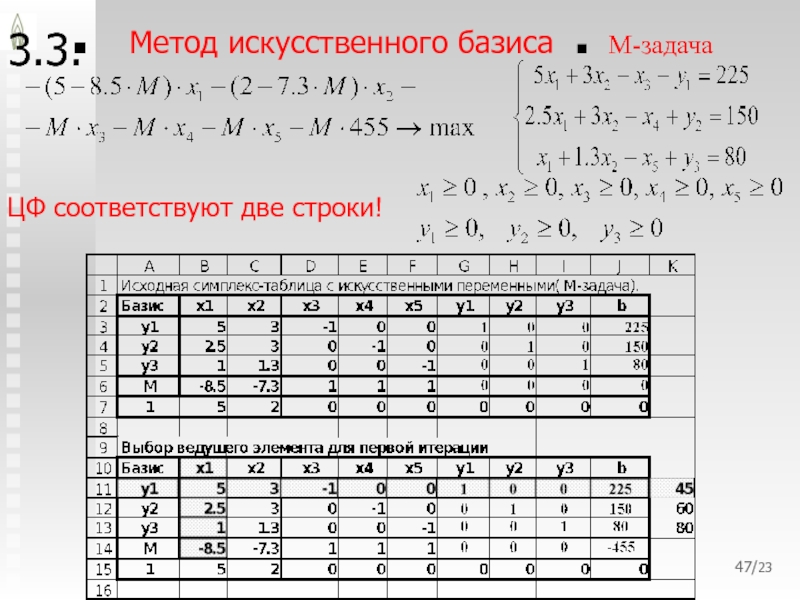
ЦФ соответствуют две строки!
Коэффициенты в ЦФ
имеют вид :
Первая строка содержит множители, стоящие перед постоянной М,
т.е. Вторая строка
Обе строки будем преобразовывать по тем же правилам, что и остальные строки.
Поскольку
положительное число, очевидно,
что знак коэффициента
полностью определяется знаком
Это определяет ход решения М-задачи:
сколь угодно большое
Слайд 46/23
3.3.
Метод искусственного базиса
,
.
,
М-задача
ход решения М-задачи:
с
▲сначала избавляемся от отрицательных
коэффициентов в первой строке ЦФ (в таблицах эта строка помечена
буквой «М»);▲ далее избавляемся от отрицательных коэффициентов во второй строке ЦФ (в таблицах эта строка помечена буквой «1»), при условии, что в этом столбце строки «М» содержится ноль.
Слайд 49/23
3.3.
Метод искусственного базиса
,
.
,
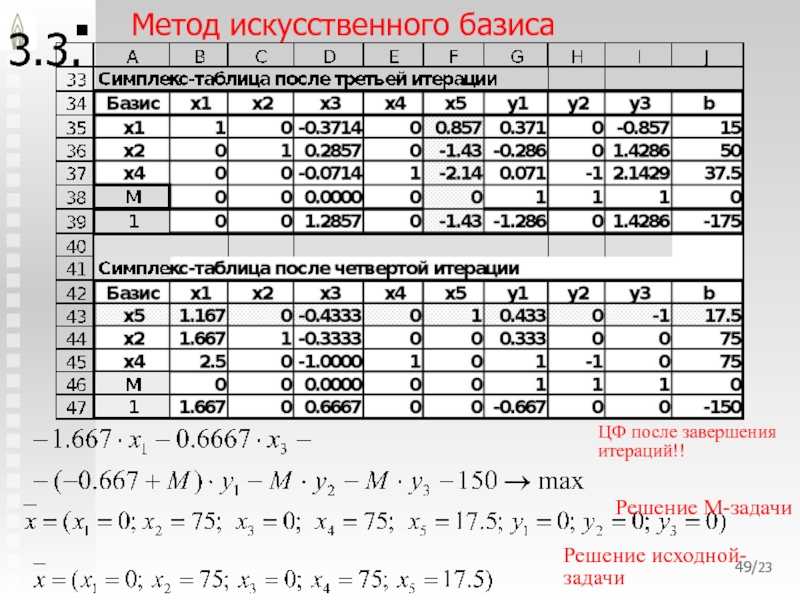
Решение М-задачи
Решение исходной-задачи
ЦФ после
завершения итераций!!
Слайд 50/23
3.3.
В некоторых случаях алгоритм симплексного метода может зацикливаться.
Пути преодоления этой
проблемы описаны в рекомендуемой литературе.
Применение линейного программирования в математических моделях
©
Н.М. Светлов, 2007-2011Слайд 51ЗАДАЧА ОБ ОПТИМАЛЬНОМ РАСПРЕДЕЛЕНИИ РЕСУРСОВ
Здесь (2.1) - целевая функция (ЦФ);
(2.2) - система ограничений; (2.3) - естественные граничные условия;
Слайд 52Двойственная задача
Правила:
Каждому i-му ограничению исходной задачи соответствует переменная двойственной
задачи ui (двойственная переменная).
Каждой j-ой переменной исходной задачи соответствует ограничение
двойственной задачи. Матрица коэффициентов ограничений двойственной задачи является транспонированной Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи.
Если исходная задача была на нахождение максимума, то двойственная будет на нахождение минимума
двойственные переменные принято называть двойственными оценками Ui
Слайд 53Двойственная задача
Правила:
1. Каждому i-му ограничению исходной задачи соответствует переменная
двойственной задачи ui (двойственная переменная).
2. Каждой j-ой переменной исходной задачи
соответствует ограничение двойственной задачи. Матрица коэффициентов ограничений двойственной задачи является транспонированной 4. Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи.
5. Если исходная задача была на нахождение максимума, то двойственная будет на нахождение минимума
двойственные переменные принято называть двойственными оценками Ui или теневой ценой
3. Коэффициенты целевой функции прямой задачи являются свободными членами (правыми частями) ограничений двойственной задачи
6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной — числу переменных прямой.
Слайд 54Двойственная задача
Теорема 1
Пусть xj, j = 1, 2,…, n
обозначает допустимый план прямой задачи, а ui, i = 1,
2,…, m – допустимый план двойственной задачи. Тогда выполняется неравенство: ,при этом на оптимальных планах всегда выполняется равенство (maxF = minG). Если хотя бы одна из задач не имеет допустимого плана, то ни одна из них не имеет оптимального решения.
Для того чтобы допустимые планы прямой и двойственной задач были оптимальными, необходимо и достаточно, чтобы выполнялись равенства
Эти условия называются условиями дополняющей нежесткости!
двойственные переменные принято называть двойственными оценками Ui
Теорема 2
Слайд 55Свойства решений (следствия из теорем двойственности!)
Значения целевых функций для оптимальных
решений прямой и двойственной задач совпадают
Двойственная оценка ui в
экономических приложениях называется теневой ценой. Теневая цена ui является коэффициентом при bi => показывает, как изменится целевая функция при изменении i-го ресурса на единицу.Теневая цена показывает предельную величину цены на данный ресурс, которую целесообразно платить за него, чтобы производство продукции давало прибыль.
Двойственная задача
Слайд 56/23
3.4. Экономические приложения линейного программирования
Матрица потребности в ресурсах для обеспечения
единичного объёма производства в каждой отрасли.
Строки – ресурсы, столбцы –
отрасли.Объёмы невоспроизводимых ресурсов (земельные угодья, трудовые ресурсы, запасы полезных ископаемых и т.п.), имеющиеся в распоряжении народного хозяйства
Матрица затрат (+) и выпуска (-) ресурсов при единичном объёме производства в каждой отрасли.
Строки – ресурсы, столбцы – отрасли.
Вектор, состоящий из нулей
Матрица выпуска (+) конечной продукции при единичном объёме производства в каждой отрасли.
Строки – виды продукции, столбцы – отрасли.
Вектор объёмов потребления каждого вида конечной продукции при единичном (стандартном) уровне удовлетворения потребностей
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 57/23
3.4. Экономические приложения линейного программирования
Вектор цен продукции (за вычетом НДС),
руб./ед.
Вектор цен ресурсов (включая НДС), руб./ед.
Матрица затрат ресурсов на производство
и реализацию единицы продукции, ед.рес./ед.прод.Вектор наличия (начальных запасов) ресурсов
Матрица объёмов обязательств, выполняемых вследствие реализации единицы продукции каждого вида
Объёмы обязательств, имеющихся у предприятия и учитываемых при оптимальном планировании (выполнение которых зависит от составленного плана)
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011
Слайд 58Применение линейного программирования в математических моделях
(с) Н.М. Светлов, 2007
/23
3.5. Программное
обеспечение линейного программирования
Запуск решения – [Ctrl]+[x]
Найти XA
Слайд 59/23
3.5.
Два способа установки XA
Если есть права доступа к каталогу C:\WINDOWS
копируем
туда файлы CXA32.DLL и CAXA32.DLL
Иначе
копируем файлы CXA32.DLL и CAXA32.DLL в
ту папку, в которой решаем модельпосле вызова файла модели нажимаем кнопку и указываем расположение любого из этих файлов
это действие повторяется при каждом вызове Excel
Антивирус Касперского блокирует выполнение XA
При первом вызове программы следует в ответ на предупреждение антивируса дать ему указание разрешать выполнение данной программы
Найти XA
Применение линейного программирования в математических моделях
© Н.М. Светлов, 2007-2011










































![Применение линейного программирования в математических моделях Применение линейного программирования в математических моделях (с) Н.М. Светлов, 2007/233.5. Программное Применение линейного программирования в математических моделях (с) Н.М. Светлов, 2007/233.5. Программное обеспечение линейного программированияЗапуск решения – [Ctrl]+[x]Найти](/img/thumbs/4687e8eb4b9216f737f2d0c8872e7a85-800x.jpg)




















