FΔt- ?
Решение
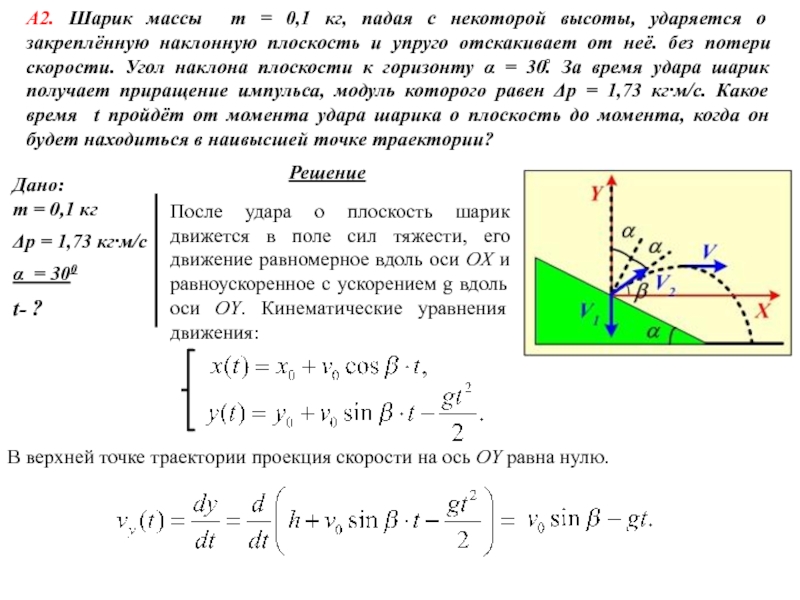
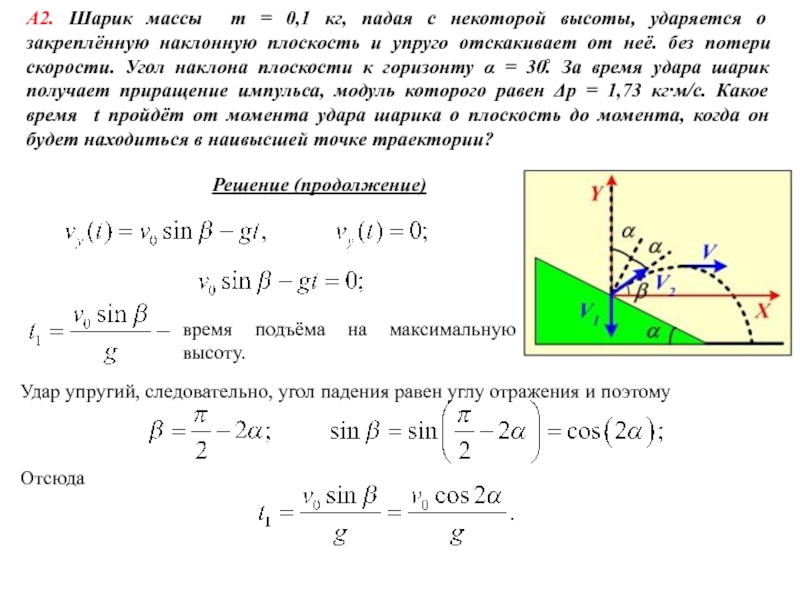
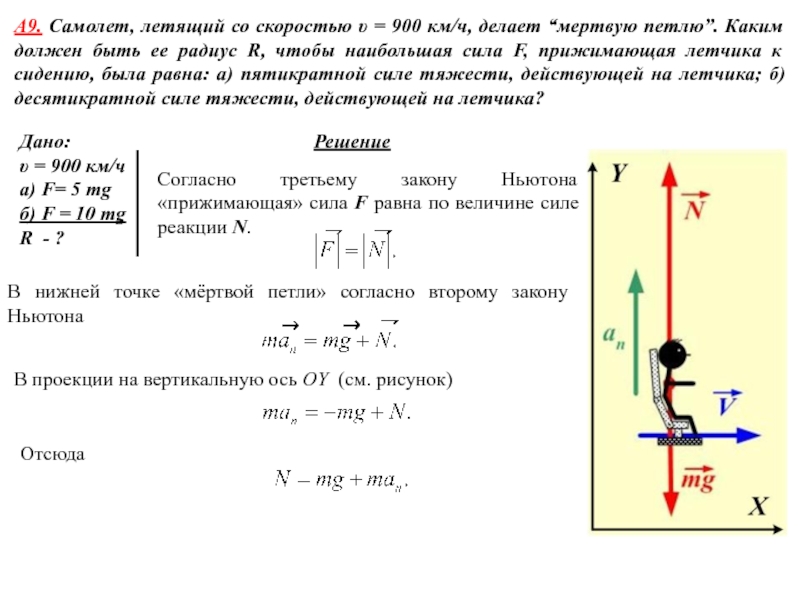
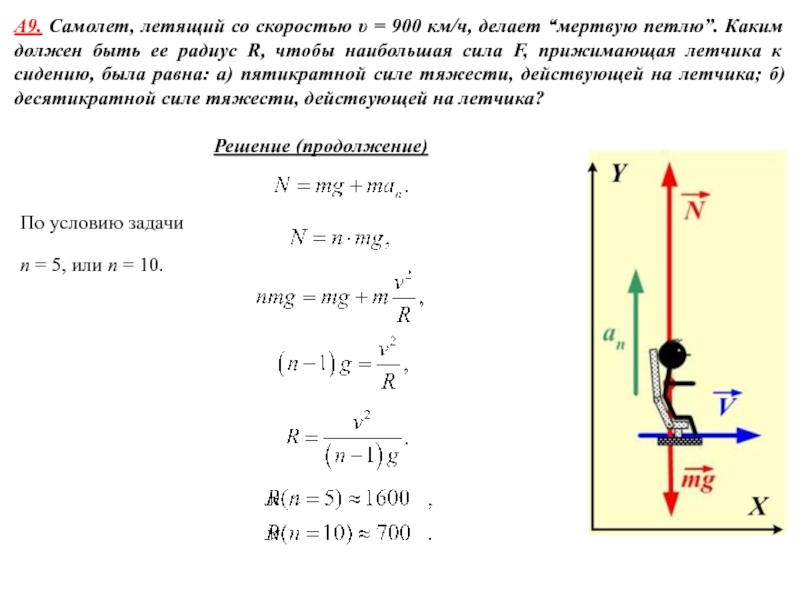
А1. Молекула массой m = 4,65⋅10-26 кг,
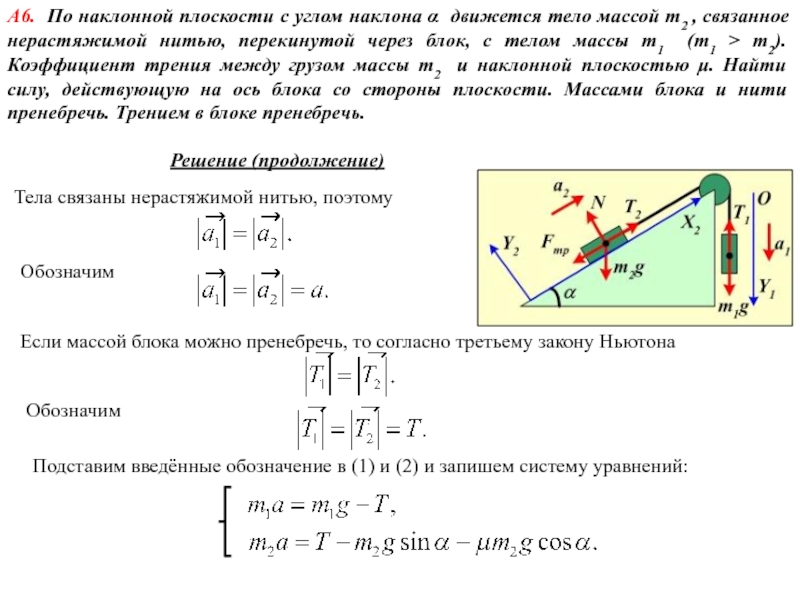
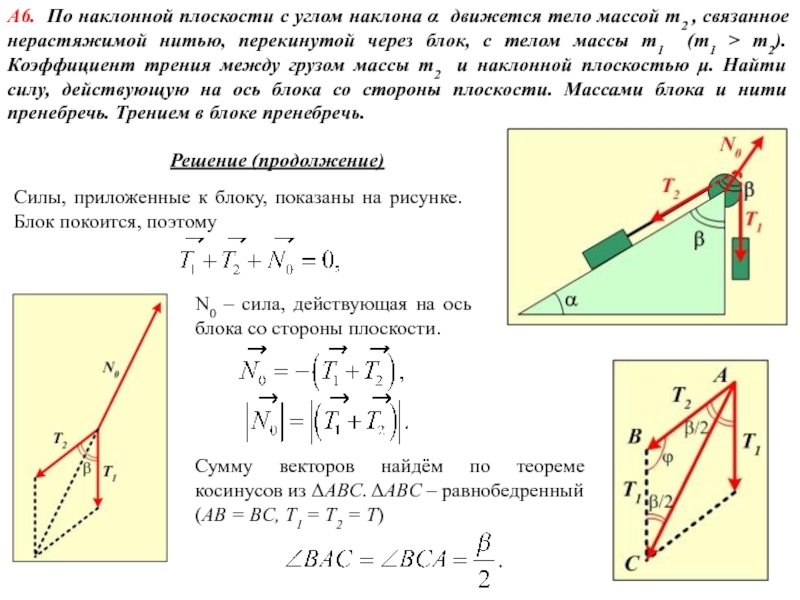
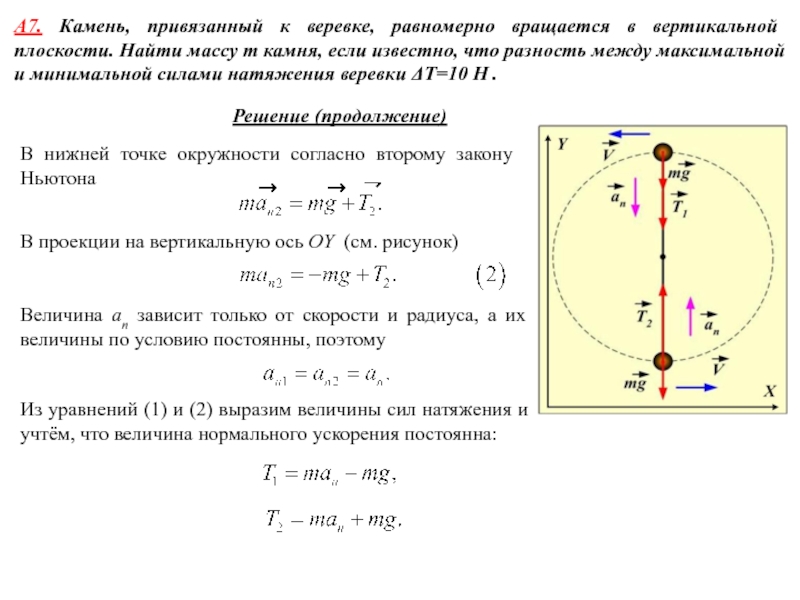
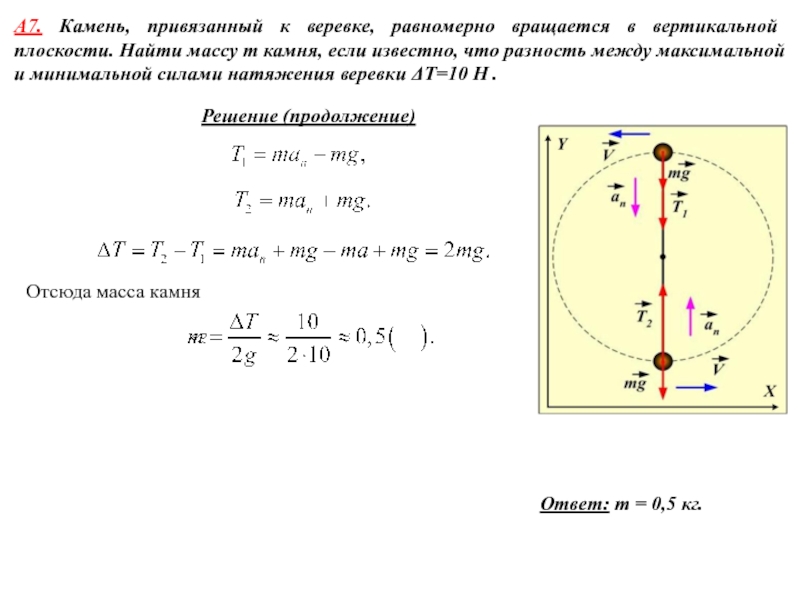
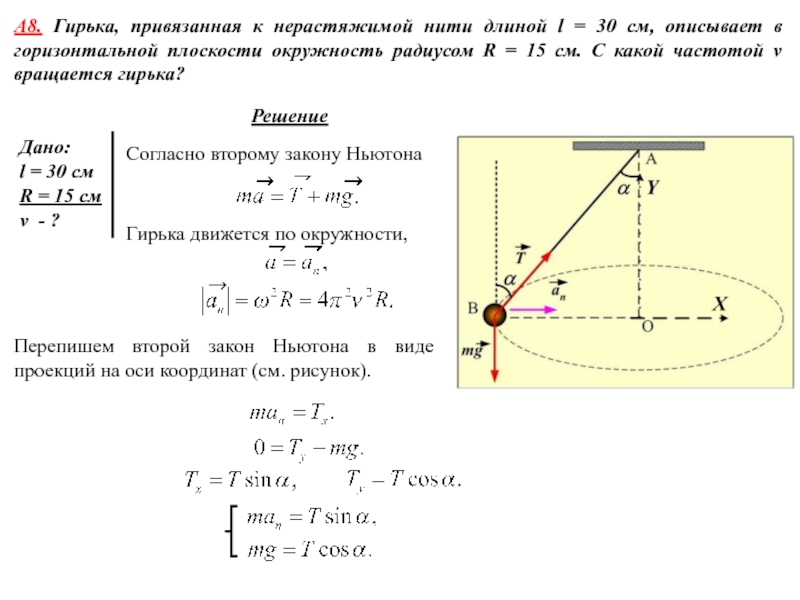
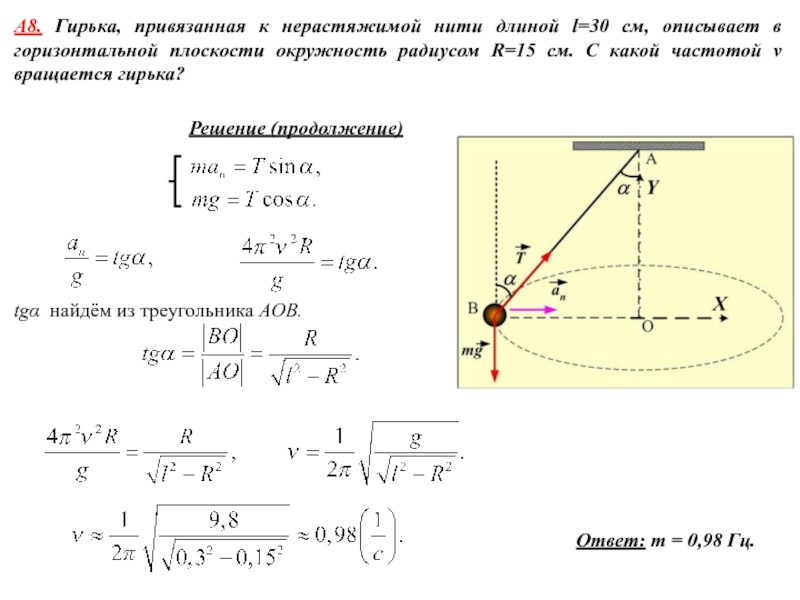
летящая со скоростью υ = 600 м/c, ударяется о стенку сосуда под углом α = 600 к нормали и упруго отскакивает от нее без потери скорости. Найти импульс силы , полученный стенкой за время удара.Используем второй закон Ньютона
Импульсом силы называется величина
Найдём приращение импульса
В проекциях на оси координат